z5_otv
реклама

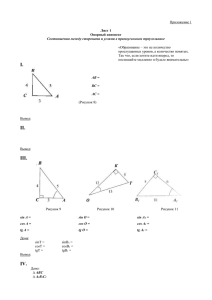
Задачи: а) Сфера с центром в точке 𝑂 касается ребер пирамиды 𝑆𝐴𝐵𝐶𝐷 в точках 𝐴, 𝐵, 𝐾, 𝐿. Точки 𝐾, 𝐿 принадлежат ребрам 𝑆𝐶 и 𝑆𝐷 соответственно, точка 𝑂 принадлежит основанию пирамиды. Докажите, что точки 𝐴, 𝐵, 𝐾, 𝐿 принадлежат одной плоскости. б) Четырехугольник 𝐴𝐵𝐶𝐷 вписан в окружность, 𝐴𝐵 = 𝐶𝐷. Докажите, что 𝐴𝐵𝐶𝐷 – трапеция. в) 𝐴𝐵𝐶𝐷 – трапеция, 𝐴𝐵 = 𝐶𝐷 = 2√5, 𝐵𝐶 = 6, 𝐴𝐷 = 2. Найдите: длину диагонали трапеции, радиус описанной окружности, длину перпендикуляра, проведенного из точки 𝐷 к прямой 𝐴𝐵. г) На сторонах 𝐵𝐶 и 𝐴𝐶 треугольника 𝐴𝐵𝐶 лежат точки 𝐾, 𝐿 соответственно, 𝐾𝐿 ∥ 𝐴𝐵, 𝐵𝐾 = 3. Найдите длину стороны 𝐵𝐶, если 𝐴𝐵 = 4, 𝐾𝐿 = 1. Проверка: а) Сфера с центром в точке 𝑂 касается ребер пирамиды 𝑆𝐴𝐵𝐶𝐷 в точках 𝐴, 𝐵, 𝐾, 𝐿. Точки 𝐾, 𝐿 принадлежат ребрам 𝑆𝐶 и 𝑆𝐷 соответственно, точка 𝑂 принадлежит основанию пирамиды. Докажите, что точки 𝐴, 𝐵, 𝐾, 𝐿 принадлежат одной плоскости. (Рисунок 2.13) Рисунок 1 Решение: 𝑆𝐴 = 𝑆𝐵 = 𝑆𝐾 = 𝑆𝐿 (как отрезки касательных) ∠𝑆𝐴𝑂 = ∠𝑆𝐵𝑂 = ∠𝑆𝐾𝑂 = ∠𝑆𝐿𝑂 = 90° (как углы между радиусом и касательной) ∆𝑆𝐴𝑂 = ∆𝑆𝐵𝑂 = ∆𝑆𝐾𝑂 = ∆𝑆𝐿𝑂 (по общей гипотенузе 𝑆𝑂 и равным 𝑆𝐴, 𝑆𝐵, 𝑆𝐾, 𝑆𝐿) В прямоугольном треугольнике 𝑆𝐴𝑂 построим высоту 𝐴𝐻, тогда отрезок 𝐵𝐻 будет являться высотой в треугольнике 𝑆𝐵𝑂. Так как 𝑆𝑂 ⊥ 𝐴𝐻, 𝐴𝐻 ∈ (𝐴𝐻𝐵) и 𝑆𝑂 ⊥ 𝐵𝐻, 𝐵𝐻 ∈ (𝐴𝐻𝐵), то 𝑆𝑂 ⊥ (𝐴𝐻𝐵). Аналогично 𝑆𝑂 ⊥ (𝐾𝐻𝐿). 𝑆𝑂 ⊥ (𝐴𝐻𝐵), 𝑆𝑂 ⊥ (𝐾𝐻𝐿) и эти плоскости проходят через точку 𝐻. Следовательно, они совпадают. б) Четырехугольник 𝐴𝐵𝐶𝐷 вписан в окружность, 𝐴𝐵 = 𝐶𝐷. Докажите, что 𝐴𝐵𝐶𝐷 – трапеция. (Рисунок 2.14) 𝐴 𝐵 𝐷 𝐶 Рисунок Error! No text of specified style in document. Решение: По условию 𝐴𝐵 = 𝐶𝐷, тогда дуги, которые стягивают эти хорды, также равны. И равны вписанные углы, опирающиеся на эти дуги, то есть, ∠𝐴𝐶𝐷 = ∠𝐴𝐶𝐵. Эти углы являются накрест лежащими при прямых 𝐵𝐶 и 𝐴𝐷, 𝐴𝐶 – секущая. Следовательно, 𝐵𝐶 ∥ 𝐴𝐷. Значит, 𝐴𝐵𝐶𝐷 – равнобедренная трапеция (𝐵𝐶 ∥ 𝐴𝐷, 𝐴𝐵 = 𝐶𝐷). в) 𝐴𝐵𝐶𝐷 – трапеция, 𝐴𝐵 = 𝐶𝐷 = 2√5, 𝐵𝐶 = 6, 𝐴𝐷 = 2. Найдите: длину диагонали трапеции, радиус описанной окружности, длину перпендикуляра, проведенного из точки 𝐷 к прямой 𝐴𝐵. (Рисунок 2.15) 𝐿 𝐴 𝐷 𝐻 𝐵 𝐶 𝑄 Рисунок 3 Решение: Построим высоту 𝐴𝑄. Найдем 𝐵𝑄 = 𝐵𝐶−𝐴𝐷 2 = 6−2 2 = 2. Тогда 𝑄𝐶 = 𝐵𝐶 − 𝐵𝑄 = 6 − 2 = 4. Из прямоугольного треугольника 𝐴𝑄𝐵 катет 𝐴𝑄 = √𝐴𝐵 2 − 𝐵𝑄 2 = √20 − 4 = 4. Из прямоугольного треугольника 𝐴𝑄𝐶 гипотенуза 𝐴𝐶 = √𝐴𝑄 2 + 𝑄𝐶 2 = √16 + 16 = 4√2. По теореме синусов найдем радиус 𝐻𝐴 окружности описанной около треугольника 𝐵𝐴𝐶, а значит, и около трапеции 𝐴𝐵𝐶𝐷: 𝐴𝐵 sin ∠𝐴𝐶𝐵 = 2 ∙ 𝐻𝐴, откуда найдем 𝐻𝐴 = √10. Соединим точки 𝐻 и 𝐵. Треугольник 𝐴𝐻𝐵 – равнобедренный (𝐴𝐻 = 𝐻𝐵 как радиусы), построим 𝐻𝐸 – медиану, высоту и биссектрису и из прямоугольного треугольника 𝐻𝐸𝐴 найдем катет 𝐻𝐸 = √𝐻𝐴2 − 𝐸𝐴2 = √10 − 5 = √5. Проведем перпендикуляр 𝐷𝐿 к стороне 𝐴𝐵, в треугольнике 𝐵𝐴𝐷 он является высотой, опущенной на продолжение стороны. Найдем его длину методом площадей (𝐵𝑍 – высота к стороне 𝐴𝐷, 𝐵𝑍 = 𝐴𝑄 = 4): 1 1 𝐵𝑍 ∙ 𝐴𝐷 = 2 𝐴𝐵 ∙ 𝐷𝐿, 2 𝐷𝐿 = г) 𝐵𝑍∙𝐴𝐷 𝐴𝐵 4∙2 = 2√5 = 4√5 5 . На сторонах 𝐵𝐶 и 𝐴𝐶 треугольника 𝐴𝐵𝐶 лежат точки 𝐾, 𝐿 соответственно, 𝐾𝐿 ∥ 𝐴𝐵, 𝐵𝐾 = 3. Найдите длину стороны 𝐵𝐶, если 𝐴𝐵 = 4, 𝐾𝐿 = 1. (Рисунок 2.16) 𝐵 𝐾 𝐴 𝐿 𝐶 Рисунок 4 Решение: ∆𝐴𝐵𝐶 ∾ ∆𝐿𝐾𝐶 с коэффициентом подобия равным 𝐵𝐶 𝐵𝐶−𝐵𝐾 𝐵𝐶 = 4, отсюда 𝐵𝐶−3 = 4, 𝐵𝐶 = 4. 𝐴𝐵 𝐾𝐿 4 = 1 = 4. Следовательно,