Динамические системы - Саратовский государственный

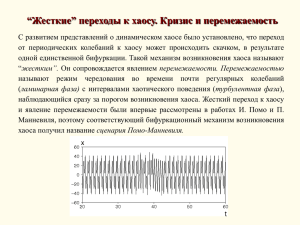
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Саратовский государственный университет имени Н.Г. Чернышевского
Физический факультет
УТВЕРЖДАЮ
Проректор СГУ по учебнометодической работе
____________________Е.Г.Елина
"__" __________________2011 г.
Рабочая программа дисциплины
Динамические системы
Направление подготовки
Физика живых систем
Профили подготовки
Биофизика, Медицинская фотоника
Квалификация (степень) выпускника
Бакалавр
Форма обучения
очная
Саратов, 2011
1
1. Цели освоения дисциплины
Целью освоения дисциплины «Динамические системы» является
приобретение знаний в области теории динамических систем и нелинейной
динамики в приложении к задачам физики живых систем, что соответствует
основным целям бакалавриата в части получении высшего профессионально
профилированного образования, позволяющего выпускнику успешно
работать в избранной сфере деятельности в РФ и за рубежом, обладать
универсальными и предметно специализированными компетенциями,
способствующими его социальной мобильности, востребованности на рынке
труда и успешной профессиональной карьере.
2. Место дисциплины в структуре ООП бакалавриата
Дисциплина «Динамические системы » входит в число дисциплин модуля
«Теоретическая биофизика» и относится к базовой части профессионального
цикла (Б3.Б.2.4.) , курс читается в 6 семестре. Форма итоговой аттестации —
зачет.
Изучаемый в рамках дисциплины теоретической и практический
материал является естественным продолжением, дисциплин, дающих
базовую подготовку в области математических методов и призван
сформировать знания и умения обучаемых в области как теоретического, так
и численного исследования детерминированной динамики математических
моделей живых систем.
Преподаваемый материал опирается на базовые знания, преподаваемые в
рамках модуля «Математика» в таких дисциплинах, как «Математический
анализ», «Дифференциальные уравнения. Интегральные уравнения и
вариационное исчисление», «Теория функций комплексного переменного».
Для успешного освоения данной дисциплины обучаемый должен
владеть
знаниями о математических методах получения и решения
обыкновенных дифференциальных уравнений, что и обеспечивается
предварительным
освоением
вышеперечисленных
дисциплин.
Преподаваемый в рамках дисциплины «Динамические системы» материал
создает необходимую теоретическую и методологическую базу для
последующего освоения дисциплин вариативной части профессионального
цикла «Нелинейная динамика живых систем», «Математические методы в
физиологии».
Полученные в результате освоения данной дисциплины знания и
навыки могут быть непосредственно применены обучающимися в их
будущей профессиональной деятельности, а при продолжении ими обучения
в магистратуре являются частью базовых знаний по
дисциплинам,
связанным с применением математических методов в системной физиологии
и динамике популяций.
2
3. Компетенции обучающегося, формируемые в результате освоения
дисциплины «Динамические системы»
В процессе освоения обучаемым дисциплины «Динамические системы»
достигается освоение общекультурных (ОК) и профессиональных (ПК)
компетенций, характеризуемых:
- способностью использовать в познавательной и профессиональной
деятельности базовые знания в области математики и естественных
наук (ОК-1);
способностью приобретать новые знания, используя современные
образовательные и информационные технологии (ОК-3);
- способностью использовать базовые теоретические знания для
решения профессиональных задач (ПК-1);
- способностью применять на практике базовые профессиональные
навыки (ПК-2);
- способностью использовать специализированные знания в области
физики для освоения профильных физических дисциплин (в
соответствии с профилем подготовки) (ПК-4);
-
способностью
применять
на
практике
базовые
общепрофессиональные знания теории и методов биофизических
исследований (в соответствии с профилем подготовки) (ПК-5);
В результате освоения дисциплины обучающийся должен:
Знать основные положения качественной теории дифференциальных
уравнений,
термины и подходы нелинейной динамики и теории
динамических систем, применяемые для анализа поведения динамических
систем; включая такие понятия как мультистабильность, автоколебания,
синхронизация, динамический хаос.
Уметь
формулировать задачи аналитического и численного
исследования динамических систем на фазовой плоскости и в трехмерном
фазовом пространстве и выбрать адекватные теоретические и численные
методы их решения.
Владеть
аналитическим методом локализации и анализа на
устойчивость
состояний
равновесия
моделей
живых
систем,
компьютерными методами анализа устойчивости периодических решений,
специализированными методами оценки меры хаотичности движения на
аттракторе в фазовом пространстве модельной системы.
4. Структура и содержание дисциплины «Динамические системы»
Общая трудоемкость дисциплины составляет 2 зачетные единицы (72 часа), в
том числе 32 часа лекций и 40 часов на самостоятельную работу.
3
4.1. Структура дисциплины
№
Раздел дисциплины
п/п
1 Введение
2 Основные понятия
3
4
5
6
7
8
теории динамических
систем
Состояния равновесия и
их устойчивость
Элементы теории
бифуркаций
Бифуркационные
механизмы рождения
автоколебаний
Синхронизация
автоколебаний и
бифуркации на торе
Детерминированный
хаос
Фракталы
Формы
текущего
контроля
Виды учебной работы,
успеваемости
включая
Сем Неделя
(по неделям
самостоятельную
естр семестра
семестра)
работу студентов и
Формы
трудоемкость (в часах)
промежуточной
аттестации (по
семестрам)
6
6
1
2
Л(2)
Л(2)
СР(2)
СР(2)
УО-1
УО-1
6
3,4
Л(4)
СР(4)
УО-1
6
5,6
Л(4)
СР(4)
УО-1
6
7,8
Л(4)
СР(4)
УО-1
6 9,10,11 Л(6)
СР(6)
УО-1
6 12,13,14 Л(6)
СР(6)
УО-1
Л(4)
СР(4)
Итоговый
зачет по
дисциплине
6
15,16
4.2. Содержание дисциплины
Раздел 1. Введение.
Понятие динамической системы (ДС).
Линейные и нелинейные ДС.
Роль методов качественной теории дифференциальных уравнений в
естествознании.
Задание ДС с непрерывным временем моделями в виде систем
обыкновенных
дифференциальных
уравнений,
дифференциальных
уравнений в частных производных. ДС с дискретным временем в виде систем
итерируемых отображений.
Раздел 2. Основные понятия теории динамических систем
4
Существование и единственность решения.
Фазовое пространство, фазовая траектория и полутраектория, особые точки,
особые и неособые траектории.
Понятие интегральной кривой. Предельные множества: аттракторы,
репеллеры и седла. Задачи качественного исследования динамической
системы.
Раздел 3. Состояния равновесия и их устойчивость.
Определение состояния равновесия. Примеры устойчивых и неустойчивых
состояний равновесия в живых системах. Анализ изменения количества и
устойчивости состояний равновесия с помощью механической аналогии
движения ширика в вязкой среде. Катастрофы складки и сборки. Процедура
аналитического поиска и анализа на устойчивость состояний равновесия в
двумерных и трехмерных системах.
Раздел 4. Элементы теории бифуркаций
Понятие структурной устойчивости и бифуркации. Понятие о точке
бифуркации и ее коразмерности. Нормальные формы. Бифуркации состояний
равновесия ДС на фазовой плоскости. Бифуркации предельных циклов и
неподвижных точек итерируемых отображений. Нелокальные бифуркации.
Раздел 5. Бифуркационные механизмы рождения автоколебаний
Мягкое рождение автоколебаний и суперкритическая бифуркация
Андронова-Хопфа. Жесткое
рождение автоколебаний, субкритическая
бифуркация Андронова-Хопфа и седлоузловая бифуркация предельных
циклов. Седлоузловая бифуркация состояний равновесия на предельном
цикле. Гомоклиническая бифуркация.
Раздел 6. Задача о синхронизации автоколебаний и бифуркации на торе
Модельные системы для изучения синхронизации. Эргодический тор как
образ двухчастотных колебаний. Отображение окружности и кольца.
Бифуркации циклов на торе и синхронизация захватом частот/фаз.
Бифуркация рождения тора и синхронизация гашением. Седлоузловые
бифуркации торов.
Раздел 7. Детерминированный хаос
История открытия динамического хаоса - краткая справка. Основное
свойство хаоса - неустойчивость фазовых траекторий. Экспоненциальное
нарастание малых возмущений, непредсказуемость, перемешивание
элементов фазового объема. Примеры модельных систем с хаотической
5
динамикой: преобразование пекаря, Cat map, логистическое отображение,
отображение окружности, отображение Хенона, биллиард Синая,
неавтономные осцилляторы типа Дуффинга, система Лоренца, система
Ресслера. Сценарии перехода к хаосу: Ландау, Релея-Такенса, Фейгенбаума.
Иллюстрация сценария Фейгенбаума с помощью спектров и фазовых
портретов. Удвоения периода в отображении. Сценарий Помо-Маневиля.
Явление перемежаемости и его иллюстрация на примере модельного
отображения. Переход к хаосу через разрушение двумерного тора.
Раздел 7. Фракталы
Задача об измерении береговой линии. Наивное определение фрактальной
размерности. Примеры фрактальных множеств: Канторово множество,
снежинка Коха, салфетка и ковер Серпинского, губка Менгера, кривые
Пеано, вселенная Фурье. Фракталы как аттракторы двумерных итерируемых
отображений. Метод случайных итераций. Сжимающие аффинные
преобразования. Лист папортника. Нелинейные комплексные отображения.
Множества Жюлиа и Мандельброта.
5. Образовательные технологии
Лекционные занятия с использованием мультимедийных средств.
Самостоятельная работа студентов выполняется в форме вычислительного
эксперимента
с
помощью
предоставляемого
обучающимся
специализированного программного обеспечения.
6. Учебно-методическое обеспечение самостоятельной работы студентов.
Оценочные средства для текущего контроля успеваемости,
промежуточной аттестации по итогам освоения дисциплины.
Наполнение объема часов самостоятельной работы предусмотрено в виде
обработки и осмысления данных, полученных в ходе лекционных занятий, а
также в виде самостоятельного проведения иллюстративных вычислений по
заданию преподавателя и с использованием предоставляемогоим
программного
обеспечения.
Текущий
контроль
успеваемости
осуществляется в виде оценки успешности выполнения практических
заданий в процессе интерактивного устного опроса.
Список контрольных вопросов по освоению основных понятий и
положений дисциплины
1.
Дайте развернутое определение понятия «динамическая система».
2.
Что такое мультистабильность?
6
3.
Какова физическая интерпретация непрерывности фазовой
траектрории?
4.
Каков смысл направления движения по фазовой траектории?
5.
Перечислите возможные бифуркации состояний равновесия на фазовой
плоскости.
6.
Охарактеризуйте метод анализа на устойчивость состояний равновесия
трехмерных систем.
Что является математическим образом автоколебаний? Дайте
7.
развернутое пояснение.
8.
Охарактеризуйте известные вам подходы к определению устойчивости
предельных циклов.
9.
Что является математическим образом двухчастотных колебаний в
фазовом пространстве?
10.
Перечислите и охарактеризуйте свойства фазового пространства,
необходимые для формирования хаотического аттрактора.
11.
Охарактеризуйте известные сценарии рождения детерминированного
хаоса.
12.
Дайте определение фрактальной размерности.
7. Учебно-методическое и информационное обеспечение дисциплины
«Динамические системы»
а) основная литература:
1. Анищенко В.С., Астахов В.В., Вадивасова Т.Е., Нейман А.Б., Стрелкова
Г.И., Шиманский-Гайер Л. Нелинейные эффекты в хаотических и
стохастических системах. - Москва-Ижевск: Институт компьютерных
исследований, 2003, 544 стр.
2.Г. А. Степаньянц. Теория динамических систем. Издательство: Либроком,
2010 г., 312 стр. ISBN 978-5-397-01414-4
3. Д.Э.Постнов. Введение в динамику итерируемых отображений.
Издательство Саратовского университета. 2007, 160с.
б) дополнительная литература:
7
1. Гласс Л., Мэки М. От часов к хаосу: Ритмы жизни: Пер. с англ. - М.: Мир,
1991. - 248 с., ил.
2. Физиология человека: В 3-х томах. Пер. с англ./ Под ред. Р.Шмидта и Г.
Тевса.- М.: Мир, 1996.- 323с., ил.
3. А.Б. Рубин. Биофизика. В 2-х кн. - М.: Высш.шк., 1987.
4. А.Б. Рубин. Лекции по биофизике. - М.: Изд-во МГУ, 1994. - 160 с.
5. Biological Psychology: Mark R. Rosenzweig, Arnold L. Leiman, S. Marc
Breedlove. Sinauer Associates, Publishers, Sunderland, Massachusetts, 1996.
Understanding Nonlinear Dynamics: Daniel Kaplan, Leon Glass. - Springer-Verlag
New York, Inc. 1995.
6. Mathematical Physiology. James Keener, James Sneyd. - Springer-Verlag New
York, Inc. 1998.
8. Материально-техническое обеспечение дисциплины
«Динамические системы»
Мультимедийный проектор, компьютер преподавателя, доступ в Интернет,
специализированное программное обеспечение для демонстрационных
вычислительных экспериментов.
Программа составлена в соответствии с требованиями ОС ВПО по
направлению Физика живых систем и ООП по профилям подготовки
Биофизика и Медицинская фотоника.
Автор:
профессор кафедры оптики и биофотоники,
д.ф.-м.н., профессор
Д.Э. Постнов
Программа одобрена на заседании кафедры оптики и биофотоники
от ___20 мая 2011____года, протокол № _______6/11___.
Подписи:
Зав. кафедрой
В.В. Тучин
Декан физического факультета
(факультет, где разработана программа)
В.М. Аникин
Декан физического факультета
(факультет, где реализуется программа)
В.М. Аникин
8