Институциональная экономика. Лекция 5

Лекция 5
Теория графов, сетей,
социальные сети и
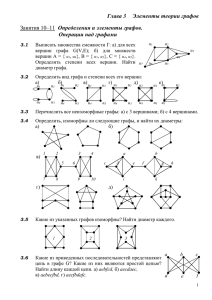
институты
План
1.
2.
3.
4.
Сети и институты
Основные понятия теории сетей
Теория графов
Матричное представление графов
Фрагмент из Facebook
Террористы, осуществившие атаки в
США 11 сентября
Авторы vec.wikipedia.org
Сети и институты
Институт предполагает наличие связей между агентами.
Наличие отношения между агентами можно
представить:
Сети и институты
Оценка количества связей отдельных агентов
позволяет строить предположения о их роли в
обществе: «фаворит» или «изгой»
Сети и институты
Для выявления экономических закономерностей
важно знать частоту взаимодействия:
Сети и институты
Взаимодействие агентов связано с издержками
(информация о партнерах, инфраструктура
связей). Поэтому система связей имеет
тенденцию к стабильности. Чем выше затраты
на организацию новых связей, тем стабильней
структура связей.
При низких затратах на организацию
взаимодействия идет поиск новых связей и
замена неудовлетворяющих.
При высоких затратах доминирует отказ от
неудовлетворительных связей и компенсация
их за счет интенсификации «хороших» связей.
Затраты на организацию связей и
их актуализация
нулевые издержки
взаимодействия
низкие издержки
взаимодействия
высокие издержки
взаимодействия
Сети и институты
Институты:
• задают ограничения на выбор агентов;
• определяют выбор агентов;
• определяют структуру устойчивых отношений
или сети.
Таким образом, сети – это форма существования
институтов.
Сети – это «дороги» взаимодействия.
Примеры: сломанный мост, взаимодействие в
организации.
Формальные и неформальные сети
Сети и институты
Сети имеют смысл:
• реальный феномен и явление социальной жизни,
которые характеризуются структурой связей и их
содержанием;
• формальный инструмент анализа силы, частоты и
возможностей агентов.
Примеры направлений анализа:
• влияние неформальных отношений между агентами на
результаты деятельности;
• оценка эффективности институциональных реформ и
социальных инноваций;
• предложения эффективной организации взаимодействия
в фирме;
• оценка роли агентов в системе связей: «центр»,
«периферия».
2. Основные понятия теории сетей
Актор – социальная единица, субъект
отношений.
Примеры акторов: люди, домохозяйства,
организации, государство.
Основная характеристика акторов целенаправленное действие.
2. Основные понятия теории сетей
Реляционная связь – связь между акторами.
Примеры:
• передача ресурсов;
• ассоциация;
• аффилирование;
• общность интересов;
• обмен информацией, знанием, взаимное обучение;
• формальные обязательства;
• доверие.
Связи между акторами могут быть реальными или
потенциальными, а их формирование может зависеть
от наличия других связей между акторами. Примеры, торговые
связи между странами, зарождение дружеских связей, доверие
и контрактные отношения.
2. Основные понятия теории сетей
Отношения - набор связей определенного типа между
акторами, принадлежащими к определенной группе.
Отношения, рассматриваемые в экономическом анализе:
• передача материальных ресурсов: заем-кредит, купляпродажа, дарение;
• передача нематериальных ресурсов: коммуникация,
обмен информацией, социальная поддержка,
покровительство;
• движение физическое (миграция) и движение
социальное (смена социального статуса, профессии
и пр.)
• родственные связи.
2. Основные понятия теории сетей
Сеть - набор акторов и отношений, которыми
они связаны.
Если это социальные отношения, то говорят
о социальной сети.
Сети могут быть однородными
и неоднородными. В однородной сети однородные участники, в неоднородной –
неоднородны.
Пример: школа и ее донор — корпорация
(отношения дарения) – неоднородная сеть.
2. Основные понятия теории сетей
Диада — простейшая сеть, состоящая из двух
участников.
С помощью диад исследуются типичные
проблемы сетей.
Примеры: уход от налогообложения через
оффшорные зоны.
2. Основные понятия теории сетей
Группа — набор акторов, чьи отношения
можно измерить.
Подгруппа — выделенный в рамках группы
более узкий набор акторов, для которых
характерен особый тип связи друг с другом.
Исследование может включать
взаимодействия не только отдельных
акторов в рамках подгрупп, но и подгрупп
между собой.
3. Теория графов
Отношения между акторами могут быть:
• ненаправленными;
• направленными.
Соответственно для анализа
применяются:
• неориентированные графы;
• ориентированные графы.
3. Теория графов. Неориентированные
графы
Граф G(N,Z)— это совокупность двух
конечных множеств: множества точек
N={n1,…,ng}, которые называются
вершинами, и множества пар вершин
Z={l1,…,ls}, которые называются ребрами.
Граф изображается точками на плоскости
и линиями, соединяющими эти точки.
Теория графов. Неориентированные
графы
Теория графов.
Неориентированные графы
Ребра, имеющие одинаковые концевые
вершины, называются параллельными.
Ребро, концевые вершины которого
совпадают, называется петлей.
Вершина и ребро называются инцидентными
друг другу, если вершина является для
этого ребра концевой точкой
Теория графов.
Неориентированные графы.
Теория графов.
Неориентированные графы.
Две вершины, являющиеся концевыми
для определенного ребра, называются
смежными вершинами.
Два ребра, инцидентные одной и той
же вершине, называются смежными
ребрами.
Теория графов.
Неориентированные графы.
Теория графов.
Неориентированные графы.
Степень ni-ой вершины d(ni) - число ребер,
инцидентных этой вершине.
Вершина степени 1 называется висячей.
Вершина степени 0 называется
изолированной.
Теория графов.
Неориентированные графы.
Теория графов.
Неориентированные графы.
Средняя степень вершин d̄ для совокупности всех
вершин графа равна:
d̄ = ∑i=1,g(d(ni) )/g
Теорема 1. В графе G сумма степеней всех
его вершин — число четное, равное удвоенному
числу ребер графа.
d̄ =2L/g
где L - общее число ребер графа;
g — общее число вершин графа.
Вариация средней степени вершин равна:
Sd2=∑i=1,g(d(ni) - d̄ )2/g
Теория графов.
Неориентированные графы.
Граф G называется полным, если любые
две его вершины соединены ребром и он
не содержит параллельных ребер.
Дополнением графа G называется граф
с теми же вершинами, что и граф G,
и содержащий только те ребра, которые
нужно добавить к графу , чтобы получился
полный граф.
Теория графов.
Неориентированные графы.
Теория графов.
Неориентированные графы.
Маршрутом между вершинами ni и nj в графе
называется последовательность ребер,
ведущая от вершины ni к вершине nj .
Длина маршрута - количество ребер в
маршруте.
Путем называется маршрут, не содержащий
циклов.
Циклом называется маршрут, начальная
и конечная вершины которого совпадают.
Теория графов.
Неориентированные графы.
Граф называется связным, если для любых двух
его вершин существует маршрут, их соединяющий.
Если существуют вершины, для которых не существует
соединяющего их маршрута, то граф называется
несвязным.
Любой несвязный граф является совокупностью таких
связных графов, которые обладают свойством:
никакая вершина одного из них не связана
маршрутом ни с какой вершиной другого. Каждый
из этих графов называется компонентой графа .
Несвязный граф.
Неориентированные графы.
Теория графов.
Неориентированные графы.
Ребро a называется мостом графа G, если
граф, получившийся из G после удаления
ребра a (обозначается G\a), содержит
больше компонент, чем граф G.
Ребро a графа G является мостом тогда
и только тогда, когда a не принадлежит
ни одному циклу.
Теория графов.
Неориентированные графы.
Коэффициент плотности графа D — является
отношением числа ребер в графе к числу
ребер в полном графе с тем же числом
вершин:
Δ=2L/g(g-1)=d̄/(g-1)
Коэффициент плотности изменяется от 0 до 1.
Единичная плотность соответствует
полному графу, нулевая — графу, в котором
все вершины изолированные.
Если отсутствуют петли и параллельные ребра
Теория графов.
Неориентированные графы.
Подграфом графа G называется граф, вершины
которого являются подмножеством вершин
графа G и ребра которого, образуя
подмножество ребер в G, соединяют
эти вершины в графе G.
Коэффициент плотности подграфа, равен
Δs=2Ls/gs(gs-1)
Δs — число ребер подграфа;
gs— число вершин подграфа.
Теория графов.
Неориентированные графы.
Теория графов.
Неориентированные графы.
Деревья - частный случай графов, содержат
минимальное количество ребер, необходимое
для связности.
У деревьев:
• любое ребро представляет собой мост;
• L=g-1;
• существует только один путь между любыми
двумя вершинами.
С помощью деревьев представляются
возможные действия игроков: дерево игры.
Теория графов.
Неориентированные графы.
Теория графов. Ориентированные
графы.
Если рассматривается множество
упорядоченных пар lk=(ni,nj) из множества
точек N={n1,ng} и на каждом ребре
из множества Z={l1,lz} задается направление,
то граф Gd=(N,Z) называется
ориентированным графом.
Если же на каждом ребре из множества Z={l1,lz}
направление не задается, то граф
G=(N,Z) называется неориентированным
графом, или просто графом
Теория графов. Ориентированные
графы.
Теория графов. Ориентированные
графы.
В ориентированном графе для каждой
вершины задаются входящие и исходящие
ребра. Характеристиками отношений для
вершины являются:
Степень захода din, равная числу ребер,
входящих в вершину;
Степень исхода dout, равная числу ребер,
исходящих из вершины.
Теория графов. Ориентированные
графы.
Теория графов. Ориентированные
графы.
Соответственно вводятся два показателя
средней степени вершин
d̄ in=∑i=1,gdin(ni)/g
d̄ out=∑i=1,gdout(ni)/g
И два показателя вариации степени вершин
S2din=∑i=1,g(din(ni)- d̄ in)2/g
S2dout=∑i=1,g(dout(ni)- d̄ out)2/g
Теория графов. Ориентированные
графы.
Коэффициент плотности ориентированного
графа равен:
Δ=L/g(g-1)
4. Матричное представление
графов
Пусть n – число акторов,
X – матрица размерности n*n,
где xij=1, если между акторами i и j есть связь,
и xij=0, если между акторами i и j нет связи.
Матричное представление
неориентированного графа
n1
n2
n3
n4
n5
n6
n1
0
0
0
0
1
1
n2
0
0
1
0
0
0
n3
0
1
0
0
0
0
n4
0
0
0
0
1
1
n5
1
0
0
1
0
1
n6
1
0
0
1
1
0
Матричное представление
ориентированного графа
Матричное представление графов
Элемент (i,j) матрицы Xm показывает
количество маршрутов длины m от актора
i к j актору .
X2 - количество маршрутов длины 2 между
акторами
X3 - количество маршрутов длины 3 между
акторами
Матричное представление графов