Мищенко (тезисы)x
реклама

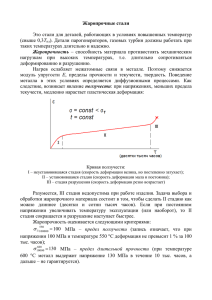
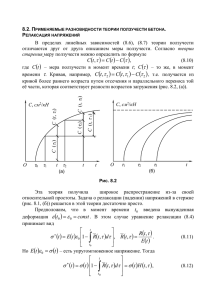
РЕШЕНИЕ ЗАДАЧ НЕУСТАНОВИВШЕЙСЯ ПОЛЗУЧЕСТИ ДЛЯ СТЕРЖНЕВЫХ СИСТЕМ НА ОСНОВЕ МОДЕЛИ С ФУНКЦИОНАЛЬНЫМИ КОНСТАНТАМИ МАТЕРИАЛОВ А.В. Мищенко, Ю.В. Немировский Новосибирский государственный архитектурно-строительный университет, 630009, Институт теоретической и прикладной механики им. С.А. Христиановича СО РАН, 630090, Новосибирск, Россия, E-mail: mavr@hnet.ru, nemirov@itam.nsc.ru Рассмотрен метод решения задач неустановившейся ползучести многослойных стержней на основе модели, содержащей начальный скачок деформации ползучести (1) c (t , T , ) (0) c (T , ) (T , )t . В частном случае при исключении первого слагаемого получаем широко распространенную модель установившейся ползучести. Начальную деформацию и постоянную скорость деформации аппроксимируем степенными зависимостями n (T ) n (T ) (0) , (T , ) B (T ) (2) c (T , ) B (T ) с четырьмя функциональными параметрами, определяемыми на основе опытных данных. Результаты обработки некоторых из них приведены в [1]. На рис. 1 пунктиром показаны линии (1), построенные по результатам обработки эксперимента [2]. В случае относительно небольшой протяженности или отсутствия второй стадии ползучести линии (1) могут рассматриваться как аппроксимации кривых ползучести в целом. ε, % 1 0.8 0.6 15 14 12 10 0.4 0.2 t, час 0 0 100 200 300 400 500 600 700 Рис. 1. Деформации ползучести стали ЭИ-69 при температуре 700оС и различных напряжениях (кгс/мм2). Точки – эксперимент, сплошные линии - модель (4), штриховые линии – модель (1). Расчет стержня Бернулли на основе модели (1) состоит из двух этапов: расчета стержня в состоянии начального скачка ползучести и ползучести с постоянной скоростью. Параметры деформированного состояния стержня в момент времени t определяются как (0) t , [u, v, , 0 , ] . В силу однотипности аппроксимаций (2) оба расчета выполняются по одинаковым (с точностью до обозначений) выражениям. Так в состоянии начального скачка деформации для s-слойного стержня получим А.В. Мищенко, Ю.В. Немировский, 2013 1 k sgn(c(0) )0 c(0) 1/ n, k (T ) B,k (T ) s N K k [ f N ( yk 1 ) f N ( yk )] k 1 Kk bk 0 (0) B,k 1/ n , k , f N ( y) 1/ n , k (T ) (0) (0) (0) c 0 y , , s M K k [ f M ( yk 1 ) f M ( yk )] (3) k 1 1 n , k n,k 1 n,k n, k f M ( y) f N ( y) y 1 2n, k (0) 0 (0) y n , k , (0) 0(0) y . (0) При замене в (3) параметров B,k , n ,k на B,k , n,k , функций (0) на (0c ) , 0 , (c) получим соотношения для расчета ползучести с установившейся постоянной скоростью. Для оценки результатов расчета по модели (1) используем описание процесса ползучести на основе теории упрочнения c c (T ) f (, T ) . Проинтегрировав и приняв степенную функцию напряжения, получим закон ( x, y, T , t ) sgn()0 [(1 k ) Bk t ] 1 nk ( x, y ) 1 k nk , (4) для которого в (3) следует принять 1 k nk bk 0 1 0 y nk , Kk , f N ( y) 1/ nk 1 k nk [(1 k ) Bk t ] nk 0 f M ( y) f N ( y) y y . 1 k 2nk Дополнив систему равенств (3) дифференциальными статическими геометрическими соотношениями N qx , Q q y , M Q mz Nv , u 0 , v , и получим замкнутую систему уравнений для решения начально-краевой задачи расчета длительно нагруженного стержня. В общем случае она требует численного решения по пространству конструкции и времени. Расчеты стержневых систем целесообразно выполнять итерационным способом на основе двухуровневой процедуры. Во внешней процедуре организуется шаговый процесс по времени, а во внутренней - решается краевая задача с использованием вместо (3) линеаризованных физических зависимостей. Для их получения напряжение представляется в эквивалентном виде E () , с переменным секущим модулем E () . Для деформации на i -м шаге внутренней процедуры, получим квазилинейный аналог системы (3): (4) [0i ] D[Ai 1] [i ] DS[i 1] N [i ] , [0i ] DS[i 1] [i ] DI[i 1] M [i ] с секущими жесткостными характеристиками сечений D[i 1] ( x) . Опуская индекс номера итерации i , для них получим s D ( x, (0) ) K k [ f ( yk 1 ) f ( yk )] , [ A, S , I ] , k 1 2 (0) f A ( y) sgn(c(0) )n,k (0) y 0 1/ n , k n, k f S ( y) f A ( y) y 1 n, k Kk , bk 0 1/ n B, k , k , (0) 0(0) y , 2n,k (0) n,k (0) f I ( y) f A ( y) y 2 0(0) y y 0(0) y . 1 2n,k 1 n,k Для стержня, показанного на рис. 2, изготовленного из стали ЭИ-69 [2], на рис. 3 показаны графики изменения максимального прогиба во времени при различной температуре. y q=0,25F/l y h F z h l Рис. 2. Схема стержня b Штриховыми линиями показаны результаты расчетов, выполненных по модели (1), а сплошными – по (4). При длительной эксплуатации модель (1) удовлетворительно согласуются с (4). v_max, мм 12 10 T=670 8 T=620 6 T=570 4 Рис. 3. Изменение максимального прогиба. Сплошная линия - модель (4), штриховая линия – модель (1). 2 t, сут 0 0 50 100 150 200 Рассмотренный здесь подход к решению задач ползучести на основе моделей с параметрами, функционально зависящими от температуры, позволяет расширить круг решаемых задач при использовании ограниченного набора экспериментальных данных; рассматривать задачи при неоднородном термо-силовом воздействии. Применение модели (1) со скачком деформации является оправданным при длительной эксплуатации. СПИСОК ЛИТЕРАТУРЫ 1. Мищенко А. В. Модель ползучести металлов с начальным скачком деформации и функциональными константами материала / А.В. Мищенко, Ю.В. Немировский // Изв. вузов. Авиационная техника, 2009. – № 1. – с. 20 – 24. 2. Никитина Л. П. Прочность стали типа ЭИ-69 при повышенных температурах / Исследования жаропрочной стали типа ЭИ-69. – М: МашГИЗ, 1947. – с. 131 – 156. Работа выполнена при поддержке гранта РФФИ, номер проекта 11-08-00186а 3