treputen x
реклама

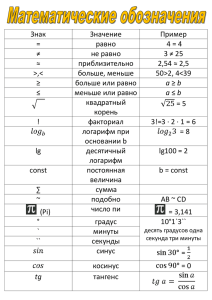
Тема: «Логарифм. Логарифм числа. Основное логарифмическое тождество.» Урок №1/32 Тип урока: урок сообщения новых знаний на основе имеющихся Цели: Обучающая: ввести понятие логарифма, изучить основные свойства логарифмов (без вывода), научить находить логарифмы данных чисел по данному основанию, упрощать выражение, используя основное логарифмическое тождество и свойства логарифмов. Развивающая: способствовать развитию логического, аналитического мышления, памяти, умения работать в заданном темпе. Воспитательная: формировать интерес к предмету, содействовать формированию личностных качеств (усидчивости, аккуратности, осознанного отношения к своей деятельности). Задачи: 1. Закрепить изученный материал, меняя виды работы, по данной теме «Логарифм. Логарифм числа. Основное логарифмическое тождество» 2. Развивать навыки и умения, в выполнении действий при изучении фигур вращения, развивать логическое мышление, правильную и грамотную математическую речь, развитие самостоятельности и уверенности в своих знаниях и умениях при выполнении разных видов работ. 3. Воспитывать интерес к математике путём введения разных видов закрепления материала: устной работой, работой с учебником, работой у доски, ответами на вопросы и умением делать самоанализ, самостоятельной работой; стимулированием и поощрением деятельности учащихся. План: I. Организационный момент. II. Новая тема: «Логарифм. Логарифм числа. Основное логарифмическое тождество.» 1.Теоретическая часть. 2.Практическая часть. III. Итог. 1. По вопросам. Ход урока I. Организационный момент. Эмоциональный настрой и готовность преподавателя и обучающихся на урок. Сообщение цели и задач. Актуализация опорных знаний II. Актуализация опорных знаний. Преподаватель: «Здравствуйте, ребята. Сегодня мы поговорим о логарифмах, но перед началом новой темы давайте вспомним, что мы знаем о степени с действительными показателями. Для этого ответим на некоторые вопросы: 1) Назовите вид простейшего показательного уравнения. ax=b 2) При каких значениях b оно имеет решение? b›0 3) Каким при этом должно быть основание степени? Основание степени всегда должно быть положительным. Преподаватель : «Записываем тему урока: «Логарифм. Логарифм числа. Основное логарифмическое тождество.» 1.Теоретическая часть. Преподаватель: Если немного перефразировать - Логарифм числа по основанию определяется как показатель степени, в которую надо возвести число , чтобы получить число (Логарифм существует только у положительных чисел). Логарифм в переводе с греческого буквально означает "число, изменяющее отношение". Преподаватель : Записываем: 1. Натуральный логарифм равное примерно 2,7 2. Десятичный логарифм - логарифм по основанию , где - число Эйлера, - логарифм по основанию 10. Свойства логарифмов: 1° - основное логарифмическое тождество. 2° 3° Логарифм единицы по любому положительному, отличному от 1, основанию равен нулю. Это возможно потому, что из любого действительного числа можно получить 1 только возведя его в нулевую степень. 4° - логарифм произведения. Логарифм произведения равен сумме логарифмов сомножителей. 5° - логарифм частного. Логарифм частного (дроби) равен разности логарифмов сомножителей. 6° - логарифм степени. Логарифм степени равен произведению показателя степени на логарифм ее основания. 7° Записываем заголовок: «Основное логарифмическое тождество» Показательное уравнение не имеет решений при и имеет единственный корень в случае, когда . Этот корень называют логарифмом числа по основанию и обозначают , то есть Итак, записываем определение: Логарифмом положительного числа по основанию ,где ›0 и ≠1, называется показатель степени, в которую нужно возвести основание , чтобы получить число . Определение Выражение с учетом того, что основным логарифмическим тождеством. Задание. Вычислить называется - , если Решение. Перепишем данное выражение, используя свойство логарифма степени и логарифма произведения: Ответ: Задание. Упростить выражение Решение. Перепишем числитель, используя свойство для степени логарифма, а знаменатель, используя свойство -логарифм произведения: Ответ. Задание. Доказать тождество: Доказательство. Приведем все логарифмы, стоящие в правой части приведенного равенства к одному основанию 3, используя формулу для замены основания логарифма: тогда выражение примет вид: Учитывая тот факт, что Согласно свойству суммы окончательный ответ В итоге: , можем записать: логарифмов получаем Что и требовалось доказать. Задание. Найти значение выражения Решение. В степени первого слагаемого разность логарифмов заменим на логарифм частного, а для второго слагаемого применим свойство логарифмов для степени основания: В полученном выражении к первому слагаемому применим основное логарифмическое тождество, а ко второму - свойство логарифма степени: учитывая, что , получим Ответ. 2.Практическая часть. Теперь работаем у доски, решаем №266. Найти логарифмы чисел по основанию 3: Вычислить: III. Итог урока Преподаватель: Давайте подведем итог нашего урока и ответим на некоторые вопросы: 1. Дайте определение логарифма числа. Ответ: Логарифмом положительного числа по основанию ,где ›0 и ≠1, называется показатель степени, в которую нужно возвести основание , чтобы получить число . 2.Перечислите основные свойства логарифмов. Ответ: Логарифм произведения равен сумме логарифмов сомножителей. Логарифм частного (дроби) равен разности логарифмов сомножителей. Логарифм степени равен произведению показателя степени на логарифм ее основания. 3. Чему равен логарифм 1? Ответ: Логарифм единицы по любому положительному, отличному от 1, основанию равен нулю. Это возможно потому, что из любого действительного числа можно получить 1 только возведя его в нулевую степень. Преподаватель: «Теперь записываем задание на дом: По учебнику «Алгебра и начала анализа 10-11 класс» Алимов Ш.А п.15,16 и решаем номера 274,276 и 292.» Рефлексия. Преподаватель: «Ребята, давайте проведем небольшое анкетирование о нашей сегодняшней работе. Посмотрите на доску и ответьте устно на вопросы» 1. На уроке я работал активно / пассивно 2. Своей работой на уроке я доволен / не доволен 3. Урок для меня показался коротким / длинным 4. За урок я не устал / устал 5. Мое настроение стало лучше / стало хуже 6. Материал урока мне был понятен / не понятен полезен / бесполезен интересен / скучен 7. Домашнее задание мне кажется легким / трудным интересным / неинтересным Спасибо за урок.