Геометрические преобразования графиков тригонометрических функций.

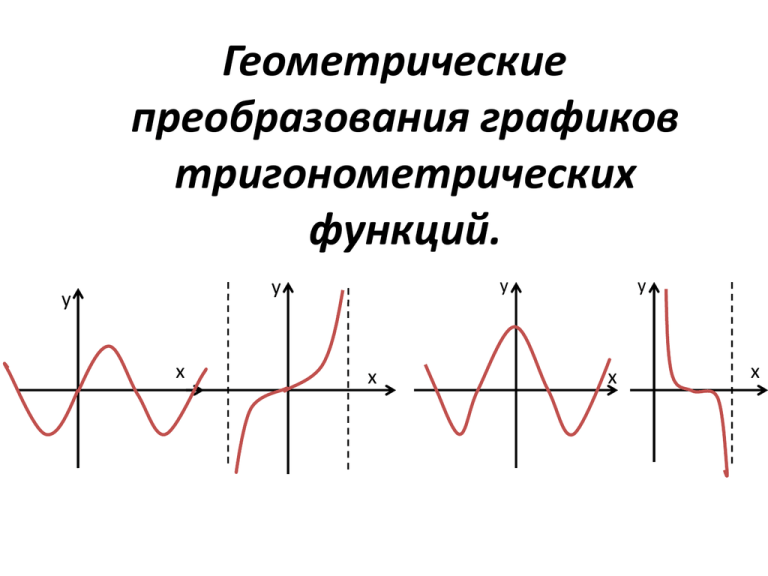
Геометрические
преобразования графиков
тригонометрических
функций.
у
у
у
х
х
у
х
х
ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ГРАФИКОВ ФУНКЦИЙ
паралельный перенос по ОУ
1) 𝑓 𝑥
паралельный перенос по ОX
2) 𝑓 𝑥
3) 𝑓 𝑥
4) 𝑓 𝑥
> f(x) + m
при 𝑚 >0 ↑; при 𝑚 <0 ↓
> f(x + m)
при 𝑚 >0 ←; при 𝑚 <0 →
сжатие, растяжение по ОУ
> аf(x)
а > 1 растяжение; 0 < а < 1 сжатие
сжатие, растяжение по ОХ
а > 1 сжатие,
5) 𝑓 𝑥
0 < а < 1 растяжение
симметрия относительно ОХ
f(аx)
> - f(x)
>
6) 𝑓 𝑥
Алгоритм:
>
|f(x)|
a)Строю Y = f(x)
b) Симметрично отображаю часть графика из нижней
полуплоскости в верхнюю.
> f|x|
7) 𝑓 𝑥
Алгоритм:
a)Рисую часть графика Y = f(x) для x ≥ 0
b) Отображаю полученную часть графика в левую
полуплоскость
У

у=х -4

4

4
4
4
44
Х
4
     4      


у=х
х
f(x)
параллельный перенос по оси ОУ
m>0
m<o
f(x)+m
f (x )
параллельный перенос по oY
f ( x)  m
при m>0 – вверх; при m<0 - вниз
y
1

П
2
П
2
-1
у = sin x + 1
x
f (x )
параллельный перенос по oY
f ( x)  m
при m>0 – вверх; при m<0 - вниз
y
1

П
2
П
2
-1
у = sin x + 1
x
f (x )
параллельный перенос по oY
f ( x)  m
при m>0 – вверх; при m<0 - вниз
у = tg x - 2
y

П
2
1
П
2
-1
x
У
4

у = |х-4|

4
4
4
 4
Х
   


у=х
х
f(x)
параллельный перенос по оси ОХ
m>0
m<o
f(x+m)
f (x )
параллельный перенос по oY
f ( x)  m
при m>0 – вверх; при m<0 - вниз
y
1

П
2
П
2
-1

y = cos ( x + 2 )
x
y  ctg ( x 
y

П
2
1
П
2
-1

2
)
x
y  ctg ( x 
y

П
2
1
П
2
-1

2
)
x
y  ctg ( x 
y

П
2
1
П
2
-1

2
)
x
f(x)=2x²
y
f(x)=x²
0
x
аf(x)
y
f(x)=x²
f(x)=0,5x²
0
x
аf(x)
f (x )
сжатие, растяжение ОY
af (x)
a>1 растяжение, 0<a<1 сжатие
y

y  2 sin x




1





П
2

П
2




-1




x

f (x )
сжатие, растяжение ОY
af (x)
a>1 растяжение, 0<a<1 сжатие
y
1
y  cos x
3
1




П
2


П
2


-1


x
f (x )
симметрия относительно ОX
 f (x )
y
1

П
2
П
2
-1
y   sin x
x
f (x )
f (аx )
y
y  sin 0,5 x
1

П
2
П
2
-1
x
f (x )
f (аx )
y
y  sin 2 x
1

П
2
П
2
-1
x
1
y

П
2
1
П
2
-1
x
2
y
1

П
2

x
П
2
П
4
-1
3П
4
3
y

П
2
1
П
2
-1
4
y
1

П
2
П
2
-1
x
6
y
3
1


П
2
П
2
3П
4
П
4
-1
4
x