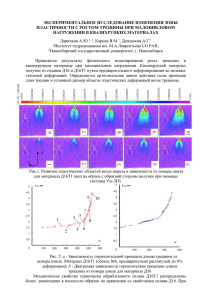
Рост трещины
реклама

Viktor M. Pestrikov Head of Informatics Department of The Saint Petersburg State University of Service and Economics, St. Petersburg, Russia. © V. M. Pestrikov Модели и критерии разрушения вязкоупругого тела с трещиной Для получения качественных и количественных характеристик процесса разрушения тела с трещиной необходимо построить модель разрушения. Модель разрушения вязкоупругого тела включает в себя: 1. Реологическую модель (уравнения) материала. 2. Модель трещины, дающую представление о форме трещины и структуре ее концевой области (зона процесса (M.Wnuk)). 3. Критерий разрушения, представляющий собой условие начала роста трещины. В качестве критериев разрушения вязкоупругих тел с трещинами могут быть использованы энергетические, силовые и деформационные. При выборе критериев разрушения следует отдать предпочтение глобальному энергетическому критерию в вариационной формулировке (E.M.Morozov, 1969), так как он в сравнении с другими критериями, позволяет полнее учесть основные особенности разрушения различных типов полимерных материалов. Глобальный критерий разрушения вязкоупругого тела с трещиной в вариационной формулировке, для трещины с тонкой зоной предразрушения перед трещиной имеет вид (Pestrikov, 1999): l (t ) a(t ) a(t ) 2 (t )dx1 pu2 ( x1,0, (t ))dx1 0 (t )u2 ( x1,0, (t ))dx1 0, (1) 0 l (t ) 0 где a(t ) l (t ) d (t ) , l (t ) - полудлина трещины, d (t ) - длина зоны предразрушения, ( (t )) - удельная работа разрушения как функция от воздействия временного фактора, вызывающего старение материала. Если предположить, что работа сил в зоне предразрушения (зона процесса, Wnuk) определяет затрату энергии на образование всей трещины, то тогда в уравнении (1) второе слагаемое много меньше третьего. В этом случае уравнение можно записать в более простом виде a t 2 ( (t )) l t 0 (t ) u2 ( x1 ,0, (t )) dx1 0.(2) l t В результате получаем локальный энергетический критерий разрушения, записанный в вариационной форме. Если теперь, в (2) варьировать время, параметр (t ) const , то получим форму записи локального энергетического критерия, удобную для практических целей: a t l t 0 d t , считая dt u2 ( x1 ,0, )dx1 2 ( )lt .(3) t Если в (2) варьировать длину трещины, при тех же допущениях, и учесть условие автомодельности, т.е. неизменности формы зоны предразрушения, du 2 du 2 , то получим: dl dx 1 2 ( (t )) 0 (t ) l a t u ( x ,0, )dx 2 1 1 0.(4) l t Отсюда следует соотношение, аналогичное известному соотношению 0 c 2 для неподвижной трещины: 0 ((t )) c ((t )) 2 ((t )), (5) где c 2u2 ((t )) – критическое раскрытие трещины. Из (5) после преобразований следует аналог силового критерия Ирвина в виде K I ( (t )) K Ic ( (t )).( 6) При исследовании разрушения вязкоупругого тела с трещиной на основе критериев (1)-(6), сначала следует выбрать реологическую модель материала. После этого определить перемещения берегов трещины в вязкоупругом материале. Если выбрана линейная теория вязкоупругости, в которой связь между напряжениями и деформациями производится с помощью интегральных операторов Вольтерра II рода, то вертикальные перемещения берегов трещины могут быть найдены из упругого решения. Вертикальные перемещения в вязкоупругом теле В общем случае запишутся в виде: вертикальные перемещения 0 (t ) u2 T ( x1, l (t )) , где ( x1, l (t )) - функция силовых и геометрических параметров, а T - интегральный оператор типа Вольтерра II рода. Реология материала Интегральный оператор для материалов в общем случае представлен в виде вязкоупругих может быть t T f (t ) T0 f (t ) K t , ( ) f ( )d , (7) 0 K t , ( ) где - ядро ползучести вязкоупругого материала с нестабильными свойствами, T0 мгновенное значение интегрального оператора, 1 v2 равное T0 E при плоской деформации и T0 1 E при плоском напряженном состоянии. Рост трещины в стареющем вязкоупругом материале Для ряда конструкционных материалов применение деформационного критерия приводит к большим погрешностям, так как во время роста трещины не соблюдается условие . Изменение раскрытия трещины во время ее роста происходит из-за деформации вблизи вершины трещины. Если считать, что затраты энергии на процесс разрушения в основном равны работе пластических деформаций в вершине трещины, то можно прийти к локальному энергетическому критерию (Knauss 1969, Wnuk 1971). Критерий разрушения стареющего вязкоупругого тела с трещиной Локальный энергетический критерий разрушения вязкоупругого тела с трещиной, для материала с изменяющимися свойствами во времени имеет вид (Pestrikov 1983) : l (t ) 0 x1 , t t u2 ( x1 , l (t ))dx1 2t l (t ), (8) L (t ) где L(t ) l (t ) d (t ) , d (t ) - длина зоны предразрушения (зона процесса Внука) Уравнение роста трещины в вязкоупругом теле с учетом особенностей старения материала Для модели трещины с тонкой структурой концевой зоны (зона процесса Внука) 1 4T0 02 l (t )tg ln sec 1 l (t ) (t ) ( 2 sec 2 tg ) 2 l (t ) (t ) (tg ln sec ) t 4l (t ) l (t )tg ln sec t0 1 R ( t , ) ( x , l ( )) dx d , (9) 1 1 l ( ) L ( ) где t 0 определяется из уравнения l t0 l t cos . Критическая длина трещины Для трещин у которых d l , критическая длина находится из условия t tc , l (t ) lc и l(t ) lc .(10) 2 4T0 0 tg ln sec Если в уравнении (9) провести преобразования и оставить величины не выше второго порядка малости, то получим уравнение роста макротрещины (d l ) в виде lc 4 d (t ) (t ) 1 2 1 l ( ) ( ) R(t , )(r )d 2 l (t ) 3 l (t ) (t ) 2l (t )( (t ) / 2) t0 t Анализ уравнений роста трещины по двум критериям Уравнение кинетики макротрещины, полученное, исходя из локального энергетического критерия (Knauss,Wnuk 1971), отличается от уравнения, полученного по деформационному критерию COD, только на величину 4 d (t ) (t ) .(11) 3 l (t ) (t ) Это различие имеет место только при переменных нагрузках. При постоянных нагрузках уравнения роста трещин совпадают. 0 и Рост трещины Диаграммы роста трещин по критерию COD (кривые 2,4) и локальному энергетическому критерию (кривые 3,5) при переменной нагрузке. Кривая 1 относится к const макротрещине при постоянной внешней нагрузке Критерий завершающего натяжения и медленный рост трещины в вязкоупругом материале Желание расширить область применимости критерия критического раскрытия трещины (COD) привели М. Внука к критерию «завершающего натяжения» (Wnuk 1974): t uP t t , t c uxP , d uxP , t uxP , t t , t t где u t t, t - критическая разность смещений в точке Р, ux , d 4 x , d , t dl и E dt структурный параметр, определяемый из эксперимента. P c P 1 P Схематическое изображение процесса разрушения по критерию «завершающего натяжения». 1 – контур трещины в момент времени , 2 – контур трещины в момент времени t. Пунктиром показаны границы зон предразрушения (зона процесса Внука) Формулировка критерия Внука Приращение нормального перемещения v в некоторой точке Р, находящейся внутри области предразрушения перед концом трещины, сохраняется постоянным в течение медленной стадии роста трещины. Уравнение докритического роста трещины исходя из критерия Внука t d c d t Qt xP , d d , t0 K I2 где d(t) длина пластической зоны в момент времени t, d t 2 и 8 2 dc K c 8 2 . ВЫВОД: Критерий «завершающего натяжения» может быть использовать при исследовании разрушения более широкого класса вязкоупругих материалов, нежели COD, в частности, для наноматериалов. End Thank you!