закон сохранения энергии система тел

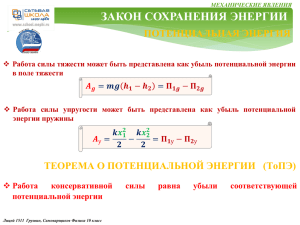
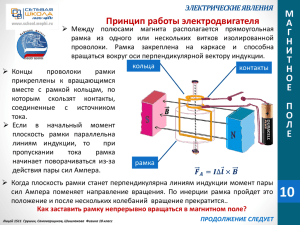
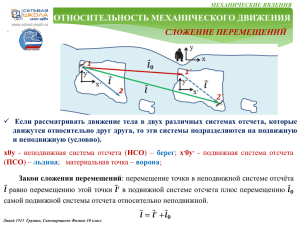
МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ
ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
СИСТЕМА ТЕЛ
 Механическая система тел (материальных точек) –
это совокупность тел, выделенных с целью решения
некоторой задачи
 Внутренние силы 𝒇𝟏𝟐 , 𝒇𝟐𝟏 , 𝒇𝟏𝟑 , 𝒇𝟑𝟏 , 𝒇𝟐𝟑 , 𝒇𝟑𝟐 , - силы,
действующие между телами, входящими в систему
 Внешние силы 𝑭𝟏 , 𝑭𝟐 , 𝑭𝟑 , - силы, действующие на
тела системы со стороны тел, не входящих в систему
 Замкнутой механической системой тел называется такая система, в которой
взаимодействуют между собой только тела, входящие в эту систему
ИМПУЛЬС СИСТЕМЫ ТЕЛ
 Импульсом системы тел называется сумма импульсов тел, составляющих эту
систему
𝒏
𝒑𝒄 = 𝒑𝟏 + 𝒑𝟐 + ⋯ + 𝒑𝒏 =
𝒑𝒊 =
𝒊=𝟏
Лицей 1511 Грушин, Самоварщиков, Храмченков Физика 10 класс
𝒏
𝒎𝒊 𝒗𝒊
𝒊=𝟏
МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ
ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
ИМПУЛЬС СИСТЕМЫ
𝒏
Закон сохранения импульса для системы тел
 Импульс
замкнутой
сохраняется
системы
𝒑𝒄 =
тел
𝒎𝒊 𝒗𝒊 = 𝐜𝐨𝐧𝐬𝐭
𝒊=𝟏
 Проекция импульса системы тел на ось 0х сохраняется если сумма проекций всех
внешних сил на эту ось равна нулю
𝒏
𝒑𝒄х =
𝒌
𝒎𝒊 𝒗𝒊х = 𝐜𝐨𝐧𝐬𝐭,
𝒊=𝟏
если
𝑭𝒋х = 𝟎
𝒋=𝟏
КИНЕТИЧЕСКАЯ ЭНЕРГИЯ СИСТЕМЫ
 Кинетическая энергия системы тел - это сумма
кинетических энергий тел, составляющих систему.
𝒎𝟏 𝒗𝟐𝟏 𝒎𝟐 𝒗𝟐𝟐
𝒎𝒏 𝒗𝟐𝒏
𝑲𝒄 = 𝑲𝟏 + 𝑲𝟐 + ⋯ + 𝑲𝒏 =
+
+ ⋯+
=
𝟐
𝟐
𝟐
Лицей 1511 Грушин, Самоварщиков, Храмченков Физика 10 класс
𝒏
𝒊=𝟏
𝒎𝒊 𝒗𝟐𝒊
𝟐
МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ
ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
МЕХАНИЧЕСКАЯ ЭНЕРГИЯ
Теорема о кинетической энергии для системы тел
 Приращение кинетической энергии системы тел в некотором процессе равно
работе всех сил, действовавших на все тела системы в течение этого процесса
Механическая энергия системы тел характеризует движение и взаимодействие тел и
является функцией скоростей и взаимного расположения тел. Она равна сумме
кинетической и потенциальной энергий тел системы.
𝑾𝒄 = 𝑲𝒄 = 𝜫𝒄
Закон сохранения механической энергии
 Полная механическая энергия замкнутой системы тел, между которыми
действуют только консервативные силы, сохраняется.
𝑾𝒄к = 𝑾𝒄н = 𝒄𝒐𝒏𝒔𝒕
 при отсутствии неконсервативных (диссипативных) сил (например, реактивных
сил, сил трения, сопротивления) механическая энергия не возникает из ничего и
не может исчезнуть в никуда.
Лицей 1511 Грушин, Самоварщиков, Храмченков Физика 10 класс
МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ
ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
РЕШЕНИЕ ЗАДАЧ
7.10. Тело массы 𝑚 = 1 кг скользит без трения по гладкой горизонтальной поверхности и въезжает на
подвижную горку (см. рисунок) массы 𝑀 = 5 кг. Высота горки 𝐻 = 1,2 м. Трение между горкой и
основанием отсутствует. Найти конечные скорости тела 𝑣 и горки 𝑢, если начальная скорость тела
𝑣0 = 5 м/с, а горка первоначально покоится.
А. Определим максимальную высоту, на
𝑚 = 1кг
 Запишем краткое условие которую поднимется тело, двигаясь по
𝑀 = 5кг
𝑹
горке
𝐻 = 1,2м
 Изобразим движение тела по горке
𝑵
𝑣0 = 5м/с
𝑥
 Изобразим силы, действующие на тела
𝜐 =?; 𝑢 = ?
 Силы тяжести
𝒎𝒈
 Силу реакции опоры
 Силы взаимодействия тел
𝑵′
𝑴𝒈
𝟏
𝟐
ℎ
𝑵 = −𝑵′ - внутренние силы системы
 При переходе системы из состояния 1 в состояние 2
выполняются:
 Закон сохранения импульса системы тел в проекции на ось 0х , т.к. внешние силы ⊥ оси 0х
 Закон сохранения механической энергии системы тел, т.к. отсутствуют неконсервативные
силы
В состоянии 1 тело движется со скоростью 𝑣0 , горка неподвижна
В состоянии 2 тело достигло максимальной высоты h и движется вместе с горкой со скоростью 𝑢0
𝑣02
𝑢02
0𝑥│𝑚𝑣0 = 𝑚𝑢0 + 𝑀𝑢0 1
𝑚
= 𝑚+𝑀
+ 𝑚𝑔ℎ 2
2
2
ПРОДОЛЖЕНИЕ СЛЕДУЕТ
Лицей 1511 Грушин, Самоварщиков, Храмченков Физика 10 класс
МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ
ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
ПРОДОЛЖЕНИЕ
РЕШЕНИЕ ЗАДАЧ
7.10. Тело массы 𝑚 = 1 кг скользит без трения по гладкой горизонтальной поверхности и въезжает на
подвижную горку (см. рисунок) массы 𝑀 = 5 кг. Высота горки 𝐻 = 1,2 м. Трение между горкой и
основанием отсутствует. Найти конечные скорости тела 𝑣 и горки 𝑢, если начальная скорость тела
𝑣0 = 5 м/с, а горка первоначально покоится.
𝑚 = 1кг
𝑚𝑣0 = 𝑚𝑢0 + 𝑀𝑢0 1
𝑣0
𝑢0
𝟐
𝟏
𝑀 = 5кг
ℎ
𝑣02
𝑢02
𝐻 = 1,2м
𝑚
= 𝑚+𝑀
+ 𝑚𝑔ℎ 2
𝑚𝑣0
2
2
𝑣0 = 5м/с
𝑢0 =
Подставим в 2 получим:
Из уравнения 1 следует:
𝑚
+
𝑀
𝜐 =?; 𝑢 = ?
𝑀 𝑣02
2
2
2
𝑚 + 𝑀 𝑣0 − 𝑚 𝑣0 = 2 𝑚 + 𝑀 𝑔ℎ ⟼ 𝑀 𝑣0 = 2 𝑚 + 𝑀 𝑔ℎ ⟼ ℎ =
=
2 𝑚+𝑀 𝑔
5 ∙ 25
=
= 1,06м ⟼ Тело не дойдет до вершины горки и съедет обратно
2 ∙ 6 ∙ 9,8
𝑢
𝑣? 𝟑
𝑥 Б. Определим конечные скорости тела и горки
 При переходе системы из состояния 1 в состояние 3 выполняются:
 Закон сохранения импульса системы тел в проекции на ось 0х , т.к. внешние силы ⊥ оси 0х
 Закон сохранения механической энергии системы тел, т.к. отсутствуют неконсервативные
силы
В состоянии 1 тело движется со скоростью 𝑣0 , горка неподвижна
В состоянии 3 горка движется со скоростью 𝑢 вправо; тело, съехав с горки, имеет скорость 𝒗
(направление скорости 𝒗 неоднозначно)
ПРОДОЛЖЕНИЕ СЛЕДУЕТ
Лицей 1511 Грушин, Самоварщиков, Храмченков Физика 10 класс
МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ
ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
ПРОДОЛЖЕНИЕ
РЕШЕНИЕ ЗАДАЧ
7.10. Тело массы 𝑚 = 1 кг скользит без трения по гладкой горизонтальной поверхности и въезжает на
подвижную горку (см. рисунок) массы 𝑀 = 5 кг. Высота горки 𝐻 = 1,2 м. Трение между горкой и
основанием отсутствует. Найти конечные скорости тела 𝑣 и горки 𝑢, если начальная скорость тела
𝑣0 = 5 м/с, а горка первоначально покоится.
0𝑥│𝑚𝑣0 = 𝑚𝑣𝑥 + 𝑀𝑢 3
𝑚 = 1кг
𝑢
𝑣0
𝑣? 𝟑
𝟏
𝑣02
𝑣𝑥2
𝑢2
𝑀 = 5кг
𝑚
=𝑚 +𝑀
4
𝐻 = 1,2м
2
2
2
𝑣0 = 5м/с
Из уравнения 4 ⟼ 𝑀𝑢2 = 𝑚 𝑣02 − 𝑣𝑥2 = 𝑚(𝑣0 − 𝑣𝑥 ) ∙ (𝑣0 + 𝑣𝑥 )
𝜐 =?; 𝑢 = ?
Из уравнения 3 ⟼ 𝑀𝑢 = 𝑚(𝑣0 − 𝑣𝑥 ) ⟼ 𝑀𝑢2 = 𝑀𝑢(𝑣0 + 𝑣𝑥 ) ⟼ 𝑢 = 𝑣0 + 𝑣𝑥
𝑚𝑣0 − 𝑚𝑣𝑥 = 𝑀 𝑣0 + 𝑣𝑥 ⟼ 𝑣0 𝑀 − 𝑚 = − 𝑣𝑥 𝑀 + 𝑚 ⟼
Подставим в 3 ⟼
𝑚−𝑀
1−5
−20
𝑣𝑥 = 𝑣0
= 5
=
= − 3,33м/с скорость тела направлена влево
𝑀+𝑚
5+1
6
2𝑚
2∙1
𝑚−𝑀
= 𝑣0
= 5∙
= 1,67м/c
Определим скорость горки: 𝑢 = 𝑣0 + 𝑣0
𝑀
+
𝑚
6
𝑀+𝑚
Ответ: 𝒗𝒙 = − 𝟑, 𝟑𝟑м/с
𝒖 = 𝟏, 𝟔𝟕м/с
В. Если тело перевалит через горку?
Лицей 1511 Грушин, Самоварщиков, Храмченков Физика 10 класс
Ответ:
𝒗𝒙 = 𝟓 м/с
𝒖=𝟎
МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ
ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
РЕШЕНИЕ ЗАДАЧ
7.17. На шар, лежащий на гладкой горизонтальной поверхности, налетает другой шар, движущийся
горизонтально. Между шарами происходит упругий центральный удар. Построить график
зависимости доли переданной энергии 𝑦 = 𝐸1/𝐸0 от отношения масс шаров 𝑥 = 𝑚1/𝑚2.
 Запишем краткое условие:
 Определим величины энергии:
2
𝑣22
𝑣
𝑥 = 𝑚1/𝑚2
𝑚1 𝐸 = 𝑚 0 Энергия налетающего шара
𝑚
2
𝐸1 = 𝑚2
0
1
2
𝑦 = 𝐸1/𝐸0
2
1
Энергия,
полученная
покоящимся
шаром
𝑣0
𝑦 𝑥 =?
𝑣 ? 2 𝑣2
𝑥
 При упругом ударе при переходе системы из состояния 1 в состояние 2 выполняются:
 Закон сохранения импульса системы тел в силу кратковременности процесса
 Закон сохранения механической энергии системы тел, т.к. отсутствуют
неконсервативные силы
 Определим 𝑣2 :
Из уравнения 1 следует:
0𝑥│𝑚1 𝑣0 = 𝑚1 𝑣𝑥 + 𝑚2 𝑣2 1
𝑚2 𝑣2
𝑣02
𝑣𝑥2
𝑣22
𝑣𝑥 = 𝑣0 −
Подставим в 2 :
𝑚1
= 𝑚1
+ 𝑚2
2
𝑚1
2
2
2
2
𝑚
𝑣
−
𝑚
𝑣
2𝑚1 𝑣0
1 0
2 2
𝑚1 𝑣02 =
+ 𝑚2 𝑣22 ⇉ 0 = −2𝑚1 𝑚2 𝑣0 𝑣2 + 𝑚22 𝑣22 + 𝑚1 𝑚2 𝑣22 ⇉
𝑣2 =
𝑚1
𝑚1 + 𝑚2
2
2 2
𝑚
𝑣
4𝑚
𝑚
𝑚2
4𝑚1 𝑣0
1 0
1 2
∙
 Определим 𝐸1 :
𝐸1 =
∙
=
2
𝑚1 + 𝑚2 2
2
𝑚1 + 𝑚2 2
𝐸1
 Определим :
𝐸1
4𝑚1 𝑚2
𝐸0
=
ПРОДОЛЖЕНИЕ СЛЕДУЕТ
𝐸0
𝑚1 + 𝑚2 2
Лицей 1511 Грушин, Самоварщиков, Храмченков Физика 10 класс
МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ
ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
РЕШЕНИЕ ЗАДАЧ
ПРОДОЛЖЕНИЕ
7.17. На шар, лежащий на гладкой горизонтальной поверхности, налетает другой шар, движущийся
горизонтально. Между шарами происходит упругий центральный удар. Построить график
зависимости доли переданной энергии 𝑦 = 𝐸1/𝐸0 от отношения масс шаров 𝑥 = 𝑚1/𝑚2.
𝑥 = 𝑚1/𝑚2
𝑦 = 𝐸1/𝐸0
𝑦 𝑥 =?
𝐸1
4𝑚1 𝑚2
=
𝐸0
𝑚1 + 𝑚2 2
𝑚1
4
𝐸1
𝑚2
=
2 ⇉
𝐸0
𝑚1
+1
𝑚2
𝑦 = 𝐸1/𝐸0
1
C учетом 𝑥 = 𝑚1/𝑚2 разделим числитель и знаменатель
на 𝑚22 , получим:
𝑬𝟏
𝟒𝒙
𝒚 𝒙 =
=
𝑬𝟎
𝒙+𝟏
Построим график
𝟐
 при х = 0, у = 0
 при х = 1, у = 1
 при х >1, у < 1
 при х → ∞, у → 0
0
1
Лицей 1511 Грушин, Самоварщиков, Храмченков Физика 10 класс
2
3
4
𝑥 = 𝑚1/𝑚2
МЕХАНИЧЕСКИЕ ЯВЛЕНИЯ
ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
РЕШЕНИЕ ЗАДАЧ
7.21. Шар, двигаясь по горизонтальной гладкой поверхности со скоростью 𝜐0, налетает на такой же
покоящийся шар. Удар абсолютно упругий нецентральный. Найти угол α разлета шаров.
𝑚1 = 𝑚2 = 𝑚
𝑣0
𝛼 =?
 Запишем краткое условие :
2
𝑢
𝑣0
1
𝑣
 При упругом ударе при переходе системы из состояния 1 до удара (вид сверху)
в состояние 2 после удара выполняются:
 Закон сохранения импульса системы тел в силу кратковременности процесса
 Закон сохранения механической энергии системы тел, т.к. отсутствуют
неконсервативные силы
𝑚𝑢
𝜋−𝜃
𝒖
𝒗𝟎
𝑚𝑣0 = 𝑚𝑣 + 𝑚𝑢 1
𝜃
𝜃
𝑚𝑣0 или
Из 1 →
2
2
2
𝑣0
𝑣
𝑢
𝑚
=𝑚 +𝑚
2
𝑚𝑣
𝒗
2
2
2
𝑣02 = 𝑣 2 + 𝑢2 − 2𝑣𝑢 ∙ 𝑐𝑜𝑠 𝜋 − 𝜃 →
И по теореме косинусов:
→ 𝑣02 = 𝑣 2 + 𝑢2 + 2𝑣𝑢 ∙ 𝑐𝑜𝑠𝜃 ∗
Из ∗ и ∗∗ →
𝑐𝑜𝑠𝜃 = 0 →
𝜃=
Лицей 1511 Грушин, Самоварщиков, Храмченков Физика 10 класс
Из 2 →
𝜋
= 900
2
𝑣02 = 𝑣 2 + 𝑢2 ∗∗
Ответ:
𝜽 = 𝟗𝟎𝟎