Максимова Н.В., МБОУ СОШ №4, Лобня
реклама

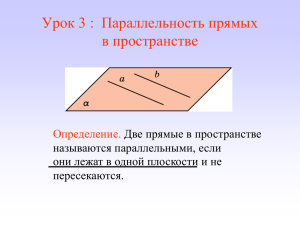
Максимова Н.В., МБОУ СОШ №4, Лобня Параллельность прямых а и b обозначаются так : а // b . На рисунке прямые а и b параллельны ,а прямые а и с ,а и d не параллельны. Рассмотрим прямую а и точку М, не лежащую на этой прямой. Через прямую а и точку М проходит плоскость , и притом только одна. Обозначим эту плоскость буквой α . Прямая, проходящая через точку М параллельно прямой а , должна лежать в одной плоскости с точкой М и прямой а , т.е. должна лежать в плоскости α . Но в плоскости α , как известно из курса планиметрии, через точку М проходит прямая , параллельная прямой а , и притом только одна . На рисунке эта прямая обозначена буквой b. Итак, b – единственная прямая , проходящая через точку М параллельно прямой а. Теорема доказана. Если две прямые параллельны третьей прямой , то они параллельны. Пусть aIIb и bIIc. Докажем, что aIIb. Для этого нужно доказать, что прямые а и b: 1) лежат в одной плоскости и 2) не пересекаются. 1) Отметим какую-нибудь точку К на прямой b и обозначим буквой α плоскость, проходящую через прямую а и точку К. Докажем, что прямая b лежит в этой плоскости. Действительно, если допустить, что прямая b пересекает плоскость α, то по лемме прямая с также пересекает плоскость α. Но так как прямые а и с параллельны, то и прямая а пересекает плоскость α, что не возможно, ибо прямая а лежит в плоскости α. 2) Прямые а и b не пересекаются, так как в противном случае через точку их пересечения проходили бы две прямые (а и b), параллельные прямой с, что не возможно. Теорема доказана. Возможны три случая взаимного расположения прямой и плоскости в пространстве : 1)прямая лежит в плоскости ; 2)прямая и плоскость имеют только одну общую точку т.е. пересекаются; 3)прямая и плоскость не имеют ни одной общей точки. ОПРЕДЕЛЕНИЕ Прямая и плоскость называются параллельными , если они не имеют общих точек. ТЕОРЕМА Если прямая , не лежащая в данной плоскости , параллельна какой-нибудь прямой , лежащей в этой плоскости , то она параллельна данной плоскости . а b b α α Рассмотрим плоскость α и две параллельные прямые a и b, расположенные так, что прямая b лежит в плоскости α, а прямая а не лежит в этой плоскости. Докажем, что а II α. Допустим, что это не так. Тогда прямая а пересекает плоскость α, а значит, по лемме о пересечении плоскости параллельными прямыми прямая b также пересекает плоскость α. Но это невозможно, так как прямая b лежит в плоскости α. Итак, прямая а не пересекает плоскость α, поэтому она параллельна этой плоскости. Теорема доказана. а b b α α 1°если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость , то линия пересечения плоскостей параллельна данной прямой . 2°.Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости , либо лежит в этой плоскости .