Студент: Шань Б.В.
реклама

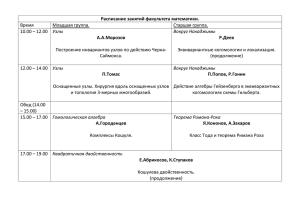
Санкт-Петербургский Государственный Политехнический Университет Расширенный метод конечных элементов (РМКЭ) Студент: Шань Б.В. Введение РМКЭ • Расширенный метод конечных элементов, разработанный Belytschko и Black [1999] на основе традиционного МКЭ, является численным методом решения дифференциальных уравнений с разрывными функциями. РМКЭ устраняет трудности при решении задач с локализованными сингулярностями, которые не эффективно решаются традиционным МКЭ. • Показано что данный метод можно использовать для решений задач, связанных с проблемой сингулярности, материальных поверхностей, где локальные особенности можно описать с помощью соответствующей кобинаци базисных функций. Разрывность и Сингулярность • Разрывные напряжения и деформации в твердых телах через материальные границы (а), разрывное перемещение у трещины (b), скорость и давление на границе двух жидкостей (с), удары и граничные слои как разрывы (d) и (e). Метод представление разрывности в РМКЭ • В РМКЭ, представление о разрывности обычно реализуется с помощью метода определения уровней (level-set method). • В качестве функции определения уровней берется такая скалярная функция, которая делит наблюдаемую область на 2 подобласти, в которых данная функция принимает разные знаки и принимает нулевое значение на разрывности Формулировка метода РМКЭ Применение XFEM для решения задачи с трещиной - Узлы элементов, содержащих вершины трещин (узлы в квадратах на рисунке), обогащаются базисными разрывными функциями. - Узлы элементов, которые пересекает трещина (узлы в окружностьях) обогащаются фукциями Хевисайда. Обогащенную аппроксимацию можно записать в следующем виде: 4 l l 4 l l u x ui N i x ai N i x H ( x) N i x bi ,1 F1 ( x) N i x bi , 2 F2 ( x) iI iL iK1 iK 2 l 1 l 1 Где: . I - множество всех узлов сетки . N - Скалярная геометрическая функция i-ого узла . L- множество узлов, обогащены фунцией Хевисайда. А ai – соответствующие степени свободы. . K1, K2 – множество узлов, принадлежащих эдементам, содержащим вершины трещины нормального отрыва (I) и поперечного сдвига (II). Соответствующие степени свободы bi,1l, bi,2l, l=1,…,4. . Функции F1l(x) и F2l(x), l=1,…,4, обогающие разрывные функции для узлов возкруг вершины трещин. F1l(x) заданы в следующем виде: h r sin ( ), r cos( ), r sin( ) sin( ), r cos( ) sin( ) 2 2 2 2 F ( x) l 1 Пример решения задачи с трещиной РМКЭ в Абакусе Размер пластины 1x1x0.01 м, начальная длина трещины 10 см. Материал: Линейно-упругий, модуль упругости 70 ГПа, коэффициент Пуасона 0.3, критическое напряжение 100 MПа. Усилие - 108 Па. Результаты вычисления Распределение напряжений по Мизесу: Выводы • При выполнении данной работы, были рассмотрены основные сведения о РМКЭ, идеализация данного метода для решения задач, связанных с разрывностью и сингулярностью. Так же была рассмотрена конкретная задача о трещине в двумерной пластине и было получено решение данной задачи в Абакусе. • Показано РМКЭ обладает большим преимуществом по сравнению с традиционным методом при решении ряд динамических задач с разрывности, в том числе задача о трещине в материалах. Список литературы • 1. http://www.xfem.rwthaachen.de/Background/Introduction/XFEM_Introduction.p hp • 2. http://www.matthewpais.com/2Dcodes • 3. http://arxiv.org/ftp/arxiv/papers/1308/1308.5208.pdf СПАСИБО ЗА ВНИМАНИЕ