Проверка корректности поведения HDL

Проверка корректности поведения
HDL-моделей цифровой аппаратуры
на основе динамического
сопоставления трасс
В.П. Иванников, А.С. Камкин
М.М. Чупилко
Содержание
•
•
•
•
•
Модели аппаратуры
Динамическая верификация
Формализация
Отношение конформности
Заключение
2/26
Модели аппаратуры
• Разрабатываются на языках проектирования
аппаратуры
– Verilog
– VHDL
• Результат проектирования – программа,
запускаемая в HDL-симуляторе
• Основной подход к верификации моделей
аппаратуры – это тестирование HDL-описаний
• Автоматизация тестирования возможна с
помощью исполнимых моделей (C/C++)
3/26
HDL-программы
input S;
output R1, R2;
void design() {
while(true) {
wait(S);
delay(6);
R1 = 1;
delay(1);
R1 = 0;
R2 = 1;
delay(1);
R2 = 0;
}
}
CLK
S
R1
R2
6 тактов
Параллельные присваивания
4/26
Поведение HDL-описания
5/26
Тестовый оракул на основе
эталонной модели
HDL
Эталонная
модель
Реакции
эталонной модели
Арбитры
реакций
Компараторы
реакций
Реакции
реализации
Адаптеры выходных интерфейсов
Стимулы
Адаптеры входных интерфейсов
Тестовый оракул
6/26
Проверка корректности поведения
Функциональные свойства
• Множества реакций корректно
• Каждая реакция корректна
• Корректный порядок реакций
• Задержки между реакциями корректны
Временные ограничения
7/26
Потактовые проверки
Реакции эталонной модели
send(R1);
3 такта
delay(3)
send(R2);
Реакции реализации
Сравнение

✕
R1
R2
R1
R2

✕
8/26
Неопределенность порядка реакций
Исполнение эталонной модели
recv(in_iface, S);
...
send(out_iface, R1);
...
Порядок реакций
R2 R1
send(out_iface, R2);
Ошибка: R2  R1
Разрешено: R2  Order
Исполнение реализации
S
R2
R1
Пересмотреть порядок
9/26
Упорядочивание реакций
• Арбитр реакций находит реакцию,
соответствующую реакции эталонной
модели
• Проверка поведения зависит от эталонной
модели и метода упорядочивания
• Арбитры реакций включают часть тестового
оракула, проверяющую порядок реакций
10/26
Типы арбитров реакций
• Детерминированный арбитр,
основанный на модели
arbiter: 2Reaction  Reaction  {fail}
• Адаптивный арбитр
arbiter: 2Reaction Reaction  Reaction  {fail}
• Двухуровневый арбитр
arbiter(reactions)  arbiter2(arbiter1(reactions), reaction)
– Недетерминированный
– Адаптивный
11/26
Детерминированный арбитр
S
R
Реакции эталонной модели
send(R1);
...
Порядок известен
R2 R1
send(R2);
Реакции реализации
Арбитр
реакций
FIFO
R1
R2
R1

✕ Сравнение
12/26
Адаптивный арбитр
S
R
Реакции эталонной модели
send(R1);
R1
Порядок неизвестен
...
send(R2);
R2
Арбитр
реакций
Get(R1)
Реакции реализации
R1
R2
R1
Подсказка

✕ Сравнение
13/26
Двухуровневый арбитр
S
R
Реакции эталонной модели
send(R1);
R1
Кандидаты
...
send(R2);
Порядок частично известен
Арбитр
#1
R2
Арбитр
#2
R1
Реакции реализации
R2
R1
Сравнение
Get(R1)

✕
Подсказка
14/26
Временное слово
 – алфавит событий
T – временной домен (R≥0, напр. N)
w = (a0, t0)(a1, t1), …  (  T)(*)
• i . ti < ti+1 (ti ≤ ti+1) – монотонность
• T i . ti > T – прогресс (если |w| = )
15/26
Частично упорядоченное
мультимножество (Pomset)
 – алфавит событий
Pomset-множество – это тройка V, , 
• V – множество вершин
•   VV – частичный порядок
• : V   – помечающая функция
16/26
Частично упорядоченное
мультимножество. Примеры
a
a
c
b
b
d
a
c
a
b
b
a
c
d
17/26
Временные трассы
 – алфавит событий, T – временной домен
Временная трасса – V, , ,  [, ]
•
V – множество вершин
•
  VV – частичный порядок
•
: V   – помечающая функция
•
: V  T – время наступления события
•
: V  T – разрешенный интервал
18/26
Поведение спецификации и
реализации
Поведение реализации
VI, , I, I
Поведение спецификации
VS, , S, S, S
Разрешенные временные интервалы
S(x) = [S(x)-t(x), S(x)+t(x)]
Соответствие событий
match(x, y) = (I(y) = S(x)) & (I(y)  S(x))
19/26
Отношение конформности
I ~ S  domI=domS ,w domS t T
M(w,t)  { (x, y)pastS(t)  pastI(t) | match(x, y) }
• взаимно однозначное бинарное отношение
• xpastS(t-t) ypastI(t) . (x, y)M(w,t)
• ypastI(t-t) xpastS(t) . (x, y)M(w,t)
• (x, y), (x’, y’) M(w,t) . x  x’  (y)  (y’)
20/26
Динамическое сопоставление трасс
• S, I – реакции спецификации и реализации для
монитора, t – монотонно возрастает
• 𝑎𝑟𝑏𝑖𝑡𝑒𝑟𝑆
𝑋
=
• 𝑎𝑟𝑏𝑖𝑡𝑒𝑟𝐼
𝑋
=
min 𝑋
если 𝑋 ≠ ∅
∅
иначе
≤
𝑎𝑟𝑔 𝑚𝑖𝑛𝑥∈𝑋.𝑚𝑎𝑡𝑐ℎ(𝑥,𝑦) 𝜃𝑆
∅
𝑥
если ∃𝑥 ∈ 𝑋. 𝑚𝑎𝑡𝑐ℎ(𝑥, 𝑦)
иначе
21/26
Проверка отношения соответствия
22/26
C++TESK Testing ToolKit
Web: http://forge.ispras.ru/projects/cpptesk-toolkit
E-mail: cpptesk-support@ispras.ru
23/26
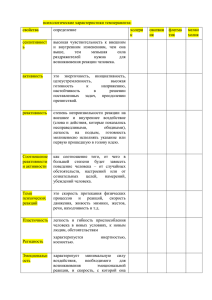
Применение инструмента
Модуль
Стадия разработки
Точность моделирования
от
до
TLB
Поздняя/завершающая
приближенная
потактовая
FPU
Поздняя/завершающая
без учета времени
--
L2
Промежуточная/поздняя
приближенная
--
DATABOX
Промежуточная/
завершающая
приближенная
потактовая
MAU
Ранняя/промежуточная
без учета времени
потактовая
IC
Ранняя/промежуточная
без учета времени
приближенная
TLU
Поздняя
приближенная
--
L2-BANK
Поздняя
потактовая
--
IB
Поздняя/завершающая
потактовая
--
L3
Промежуточная
приближенная
-24/26
Заключение
• Разработан метод динамического анализа
аппаратуры на основе теории частично
упорядоченных мультимножеств
• Метод был реализован в инструменте
C++TESK Testing ToolKit и успешно применен
в ряде проектов
• Дальнейшие исследования связаны с
диагностикой ошибок и подсказками для их
локализации
25/26
СПАСИБО!
Вопросы?
26/26