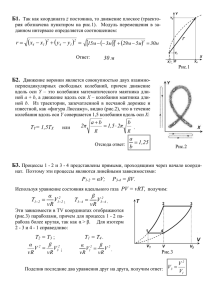
Т 2 = 340К. Температура окружающего воздуха
реклама

Семинар решения задач по физике. КОИРО. Февраль. Темы задач: 1-2. Уравнение состояния идеального газа. Динамика. 3-4. Газовые законы. Изохорный процесс. 5-6. Термодинамика. К.П.Д. – цикла. 7-8. Термодинамика. Влажность. Сорокин В.А., учитель физики, МБОУ Лицей №17 Задача №1. Шар объёмом V =0,1м3, сделанный из тонкой бумаги, наполняют горячим воздухом, имеющим температуру - Т2 = 340К. Температура окружающего воздуха – Т1= 290К. Давление воздуха внутри шара и отмосферное давление равны 105Па. При каком значении массы m ,оболочки шар будет подниматься? Решение: Чтобы шар начал подниматься, сила тяжести, действующая на него должна быть меньше или равна силе Архимеда → (m + mВ)*g = P В*g*V, тогда m = P В*V –mВ ; mВ – масса воздуха в шаре, V – объём шара, P в – плотность окружающего шар воздуха, g – ускорение свободного падения. Недостающие данные получим из уравнения состояния идеального газа → mВ = (Р*V*µ)/R*T2; P в = (Р*µ)/R*T1. Р – давление воздуха, µ -молярная масса воздуха = 0,029кг/моль, R =8,31Дж/мольК., Т – температура воздуха. Подставляя их в выделенное выражение, после преобразований получим → m = (P*V*µ)*(1/T1 -1/T2)/R В результате вычислений получим ответ m = 18г. Ответ: если масса оболочки будет меньше или равна 18г, то шар будет подниматься. Задача№2. Лёгкую сферу массой 80г взвешивают в воздухе при температуре 470С. Вес сферы оказался равным 0,1Н. При какой температуре воздуха сфера перестанет давить на чашку весов? Решение: На сферу действуют три силы : сила тяжести –m*g, сила реакции опоры N и сила Архимеда FA. Сила реакции опоры Nпо модулю равна весу тела Р. Согласно условию задачи Р1 = m*g – FA = m*g – P1*g*V и Р2= 0 = m*g – P2*g*V, где m – масса сферы, g –ускорение свободного падения, P – плотность окружающего воздуха, зависящая от температуры воздуха, V – объём сферы. Преобразуем выражения → P 1*g*V = m*g - Р1 и P 2*g*V = m*g. Разделим первое на второе → P 1/ P 2= 1- Р1/ m*g. (1) С другой стороны выразим плотность воздуха из уравнения состояния идеального газа → P =РА*µ/R*T, где РА – давление воздуха, µ - его молярная масса, R – газовая постоянная, T – температура окружающего воздуха. Тогда «навешивая индексы» и разделив одно на другое получим P 1/ P 2 = Т2/Т1 (2). Сравнивая (1) и (2) имеем 1- Р1/ m*g = Т2/Т1 отсюда Т2 = Т1*(1- Р1/ m*g). Подставляя числовые значения, получим - Ответ: Т2 = 280К или t =70C,то есть, чтобы сфера перестала давить на чашу весов, температура окружающего воздуха должна понизиться. Задача №3. С какой максимальной силой прижимается к телу человека медицинская банка, если диаметр её отверстия D =4см. В момент прикладывания к телу человека воздух в ней прогрет до температуры t1=800С, а температура окружающего воздуха t0 =200С. Атмосферное давление равно 105Па. Изменением объёма воздуха в банке пренебречь. Решение: Идея: Температура Т1 нагретого воздуха, находящегося под атмосферным давлением Р0 с течением времени уменьшается, и его давление Р становится меньше атмосферного. По условию задачи V-const. → Р0/Т1 = Р/Т0, где Т1 = 273 +80 =353К; Т0 = 273+20 =293К, Р – давление воздуха в банке после остывания, которое и надо найти. → Р =Р0*Т0/Т1. Теперь можно найти разность давлений Р0 – Р = Р0 - Р0*Т0/Т1 = Р0*(1 - Т0/Т1). По определению давления Р =F/S, → F = Р0*(1 - Т0/Т1)*S; но площадь S = π*D2/4 и в итоге F = Р0*(1 - Т0/Т1)* π*D2/4. Подставляя числовые значения, получаем ответ. F = 21Н. То есть медицинская банка присасывается к телу человека с силой 21Н. Задача №4. В цилиндре под поршнем находится воздух при давлении Р =200кПа и температуре 270С. Какой массы груз надо положить на поршень после нагревания воздуха до 500С, чтобы объём воздуха в цилиндре остался прежним? Площадь поршня S=30см2. воздух Запишем уравнение состояния воздуха до нагревания (Р0 +М1*g/S)*V = m*R *T1/µ; где Р0 – отмосферное давление, М1 – масса поршня, V – объём воздуха, S - площадь поршня, T1 – начальная температура воздуха, µ -молярная масса воздуха. R – газовая постоянная. Соответственно после нагревания (Р0 +М2*g/S)*V = m*R *T2/µ, где М2 – масса поршня с грузом, T2 – конечная температура воздуха. Разделим верхнее на нижнее → (Р0 +М2*g/S)/ Р0 +М1*g/S = T2/ T1. Но Р0 +М1*g/S =Р → Р0 = Р - М1*g/S. После подстановки получим T2/ T1 = (Р + (М2 - М1)*g/S)/Р. где М2 - М1 = ΔМ - масса груза, которую и надо найти. → ΔМ = (T2/ T1 – 1)* Р*S/g. Подставляя числовые значения получим ответ: ΔМ = 4,6кг. Задача №5. Тепловая машина совершает цикл, изображённый на PV – диаграмме. Рабочее тело – одноатомный идеальный газ. Чему равен К.П.Д. цикла? Р0 Р0 3 2 V0 1 4V0 Решение: По определению К.П.Д. = η =А./Qпол.*100%, где А – работа газа за цикл, Qпол. – количество теплоты, получаемое газом от нагревателя за цикл. Работа газа численно равна площади фигуры → А = 1,5Р0*V0. Выясним – получает или отдаёт газ количество теплоты на каждом участке цикла: → на (1-2) и (3-1) -газ отдаёт, а на (2-3) – получает количество теплоты, → нам надо вычислить Q2-3. Его можно найти, используя первый закон термодинамики, → ΔU2-3 = Q2-3 – A2-3 → Q2-3 = ΔU2-3 + A2-3 = 1,5*ʋ*R*(T3 – T2) + 9*Р0*V0/2. Но ʋ*R*T3 = 8 Р0*V0 и ʋ*R*T2 = Р0*V0 тогда Q2-3 = 9*Р0*V0/2 + 21* Р0*V0/2 = 15 Р0*V0. В результате η = (1,5Р0*V0)/( 15 Р0*V0) = 0,1 или η = 10%. Ответ: К.П.Д. = 10%. Задача №6. К.П.Д. тепловой машины, работающей по циклу: 1-2 – изотерма, 2-3-изохора, 3-1-адиабата равен η = 25%. Работа, совершённая ʋ =2моль одноатомного газа в изотермическом процессе А1-2 = 16,62кДж. Найти разность максимальной и минимальной температур. Р 1 2 3 Решение: Рассматривая цикл видно, что температура Т1 = Т2 будут максимальными, а температура Т3 есть минимальная → нам надо искать разность Т1 – Т3 = ΔТ V По определению К.П.Д. = η =А./Qпол.*100%, где А – работа газа за цикл, Qпол. – количество теплоты, получаемое газом от нагревателя за цикл → η =(А1-2 +А2-3 +А3-1)/ Q1-2, Но А2-3 =0, а А3-1 ˂ 0 и Qпол. = А1-2 в итоге η =( А1-2 - А3-1)/ А1-2 Процесс (3-1) адиабатный → А3-1 = ΔU3-1 = 1,5*ʋ*R*(T1-T3) = 1,5*ʋ*R*ΔТ, где R – газовая постоянная. После подстановки получим η = (А1-2 -1,5*ʋ*R* ΔТ )/ А1-2. Получили уравнение, в котором только одно неизвестное, → ΔТ =(2*(1 –η)* А1-2) /(3 ʋ*R). Подстановка числовых значений даёт. Ответ: Т1 – Т3 = ΔТ = 500К. Задача№7. На электрической плитке мощностью N=1кВт кипит чайник с водой. Найти скорость истечения пара из носика чайника. Площадь сечения носика чайника S=1см2. Давление на конце носика чайника равно атмосферному давлению. Считать, что вся теплота, выделяемая плиткой, передаётся воде. Решение: Ток совершает работу, и эта работа идёт на испарение воды → N*t = r*m, где r – удельная теплота парообразования воды, m- масса испарившейся воды, t – время кипения воды, N – мощность плитки. Считая водяной пар идеальным газом, запишем уравнение состояния РV = m*R*T/µ, где Р – давление газа, V – его объём, R – газовая постоянная, T температура, µ - молярная масса воды. Но V = S*L =S* v *t, в результате получаем Р* S*v*t = R*T*N*t/( µ* r), где v – скорость истечения пара. Выражая 𝓿, получим ответ v =N*R*T/(r*µ*P*S). Подставляя числовые значения, имеем v = (1*103*8,31*373) /(2,3*106*18*103*105*10-4) =7,5(м/с). Ответ: v = 7,5м/с. Задача №8. В сосуде вместимостью 100л при температуре 300С находится воздух с относительной влажностью φ = 30%. Какой будет относительная влажность воздуха в сосуде, если в него ввести воду массой 1г? Решение: ( Первый способ). Считая воздух идеальным газом, запишем уравнение состояния идеального газа → Р1*V = m1*R *T/µ, где Р1 – давление воздуха, при относительной влажности 30%, V – объём воздуха, m1 – его масса, R – газовая постоянная, T = 273 +30 =303(К) – температура, µ - молярная масса. Давление Р1 выразим через относительную влажность и Рн.п. – давление насыщенного пара, → Р1 = φ1* Р2., (Рн.п. = 4,2*103Па - из таблицы). Тогда m1 = (φ1*Рн.п.*V*µ)/(R *T). После введения в сосуд 1г воды и, соответственно её испарения получим «новое» уравнение состояния Р2*V = m2*R *T/µ, но m2 = m1 + Δm → Р2 = Р1 + (Δm*R*T)/(µ*V). Зная «новое» давление Р2 находим «новую» влажность φ2 = Р2/ Рн.п. = φ1 +(Δm*R*T)/(µ*V*Рн.п.). Подставляя числовые значения получим ответ φ2 = 63%. (Второй способ). Используем другое определение относительной влажности → φ1 =P1/ P н.п., где P 1 – плотность водяного пара, P н.п - плотность насыщенного пара при температуре t =300С, из таблиц P н.п = 30,4*10-3кг/м3. Но P 1 = m1/V → φ1 = m1/(V* P н.п ) в результате m1 = φ1*V* P н.п. При введении воды Δm получим φ2 = m2/(V* P н.п ) = (m1+ Δm)/ (V* P н.п) = φ1 + Δm/ (V* P н.п). Подставляя числовые значения, следует тот же: Ответ:φ2 = 63%