Определение Случайная величина имеет нормальное распределение вероятностей с параметрами и
реклама
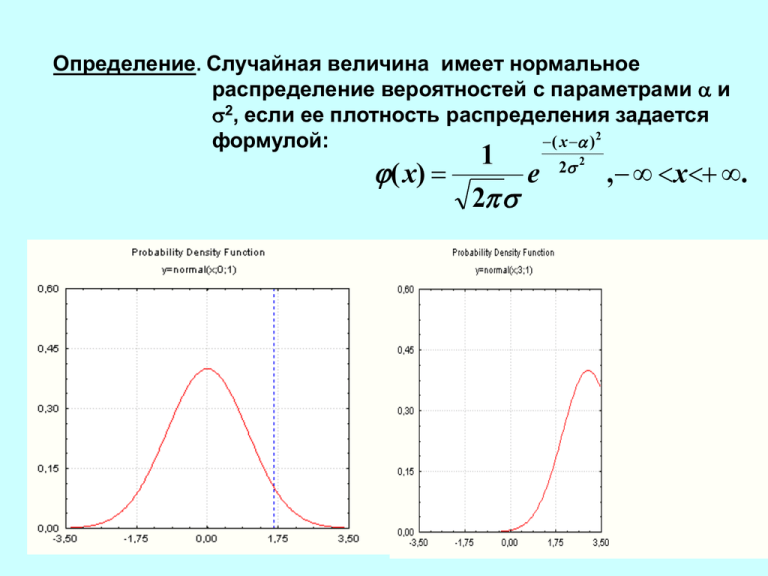
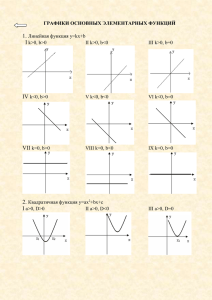
Определение. Случайная величина имеет нормальное распределение вероятностей с параметрами и 2, если ее плотность распределения задается ( x ) 2 формулой: 1 ( x) e 2 2 2 , x . Определение. Пусть 1 ,, m ; 1 ,, n (где натуральные числа) обозначают независимые случайные величины, каждая из которых распределена по стандартному нормальному закону Fm ,n (12 m2 ) , 2 2 (1 n ) 1 m 1 n Если величина стандартизирована zi xi x 2 Тогда переход к стандартному нормальному закону распределения – N (0, 2). Проверка нормальности распределения – основа критерий хи-квадрат 2 Статистическая независимость и выявление тренда 2.1 Критерий серий Если x i x то (+), если x i x то (-). ++ - ++ - +++ -+ -- + -- + --- N=20, r=12. Определение. Серией называют последовательность наблюдений перед и после которой следуют наблюдения противоположного типа. 2 N 1 N 2 (2 N1 N 2 N ) 2N1 N 2 2 r 1 (*) r 2 N ( N 1) N (**) [rn;1 rрасч rn; ] 2 2 N n 2 2.2. Критерий инверсий Пусть есть 8 наблюдений: x1=5, x2=3, x3=8, x4=9, x5=4, x6=1, x7=7, x8=5. A1 = 3, A2 = 1, A3 = 4, A4 = 4, A5 = 1, A6 = 0, A7 = 1. hij = 1, xi > xj 0, xi xj, Ai N h j i 1 N ( N 1) - мат. A ожидание 4 ij N 1 A Ai i 1 N ( 2 N 5)( N 1) 72 2 A [ AN ;1 Aрасч AN ; ] 2 2 2.3 Проверка стационарности случайного процесса. 1. Реализация x(t) разделяется на N равных интервалов. 2. Вычисляются оценки среднего квадрата для каждого интервала. Эти оценки располагают в порядке возрастания номера интервала: 2 2 2 x 1 , x 2 ,..., x N 3. Эта последовательность проверяется на наличие тренда с помощью критерия серий или критерия инверсий МЕТОДЫ МНОГОМЕРНОГО РАЗВЕДОЧНОГО АНАЛИЗА ДАННЫХ - пошаговая линейная и нелинейная регрессия - факторный анализ - кластерный анализ -анализ дискриминантных функций - многомерное шкалирование - логлинейный анализ - канонические корреляции -анализ соответствий - анализ временных рядов -деревья классификации -нейронные сети 3 РЕГРЕССИОННЫЙ АНАЛИЗ 3.1 Простая линейная регрессия ИДЕЯ Х1 Y 1 шаг. Диаграмма рассеивания Модель линейного перехода 2 шаг Расчет коэффициента парной корреляции N rxy (x i 1 i x )( yi y ) x y Предполагается модель y 0 1 x e Рассчитывается модель вида y b0 b1 x Базовый метод расчета коэффициентов модели МНК Пусть мы имеем n наблюдений величин х и y yi 0 1 xi ei , i 1,..., n (1) Y Xi X y n n S e ( yi 0 1 xi ) i 1 2 i x n S 2 ( yi 0 1 xi ), 0 i 1 n S 2 xi ( yi 0 1 xi ) 1 i 1 i 1 MIN 2 n ( y i 1 i 0 1 x i ) 0, (*) n x (y i i 1 n i 0 1 xi ) 0 n y nb b x i 1 i 0 1 i 1 i 0 (**) n n n x y b x b x i 1 i i 0 i 1 i 1 i 1 2 i 0 нормальное уравнение b1 ( x x )( y y ) ( x x) i i 2 i b0 y b1 x 3.2 Исследование полученной модели 1. Проверка адекватности полученной модели 2. Проверка корректности применения метода МНК 3. Исследование точности прогнозирования по модели 3.2.2 Проверка адекватности полученной модели ПОЛУЧИЛИ МОДЕЛЬ y b0 b1 x Определение. Под адекватностью модели простой линейной регрессии понимается, что никакая другая модель не дает значительного улучшения в предсказании Y. Номер опыта yi – результаты наблюдений - y расчетные значения yi y i 1 2 … … … … n y y yi ОСТАТКИ 1) ПРОВЕРКА ОСТАТКОВ n ( y i 1 i yi ) 0 2) ПОСТРОЕНИЕ ДИСПЕРСИОННОЙ ТАБЛИЦЫ Источник дисперсии Сумма квадратов Регрессия n ^ SS D ( yi y ) Степ. Своб. 2 i 1 Отклонение от SS R регрессии Полная n 2 ( y y ) i i D=1 R=n-2 SST ( yi y ) 2 i 1 MS D SSD SS R MS R S R 2 i 1 n Средние квадраты T=n-1 F-отношение MS D F0 MS R ПРОВЕРЯЕТСЯ ГИПОТЕЗА H0: 1=0 ПРОТИВ ЛИНЕЙНАЯ РЕГРЕССИЯ ОТСУТСТВУЕТ Если H1: 10 ЛИНЕЙНАЯ РЕГРЕССИЯ F0 Fтабл ., то гипотеза H0 отвергается. 3) Расчет коэффициента детерминации SS R R SST 2 4) Расчет доверительных интервалов для коэффициентов модели n D(b1 ) S 2 n 2 ( x x ) i i 1 дисперсия коэффициента b1: S2 2 ( y b b x ) i 0 1 i i 1 n2 b1 D(b1 ) t (1 2 :n 2 ) Доверительный интервал для b1 n D(b0 ) S 2 x i2 i 1 n n ( xi x )2 i 1 Доверительный интервал для b0 b0 D(b0 ) t( n2;1 2) Доверительный интервал для предсказываемой переменной Случай 1. Проверяется модель . y 0 1 X e Нет неадекватности. Линейная регрессия значима. Случай 2. Проверяется та же модель . Линейная регрессия незначима. Используется y 0 1 X 11 X 2 e Случай 3. Проверяется та же модель . Нет неадекватности. Линейная регрессия незначима. Используется модель y 0 1 X 11 X e 2