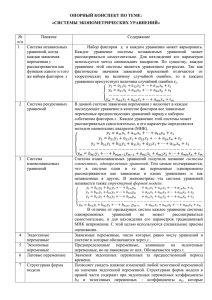
Применение систем эконометрических уравнений
реклама

Методы оценивания параметров систем эконометрических уравнений • косвенный метод наименьших квадратов – КМНК (для оценивания параметров структурной модели, для идентифицируемой модели) – структурная модель преобразовывается в приведенную – для каждого уравнения приведенной модели применяем МНК – по коэффициентам приведенной модели находим коэффициенты структурной модели • двухшаговый метод наименьших квадратов ДМНК (для оценивания параметров структурной модели, для сверхидентифицируемой структурной модели) • по приведенной модели получаем оценки эндогенных переменных • подставляем найденные значения в правые части структурных уравнений и применяем МНК • Замечание: • если все уравнения сверхидентифицируемые, то ДМНК используется для оценки структурных коэффициентов каждого уравнения; • если в системе есть точно идентифицируемые уравнения, то для этих уранений структурные коэффициенты находятся из системы приведенных уравнений. • метод максимального правдоподобия с полной информацией • метод максимального правдоподобия при ограниченной информации ММП- метод оценивания неизвестного параметра путём максимизации функции правдоподобия • функция правдоподобия - функция выражающая плотность вероятности (вероятность) совместного появления результатов выборки • результаты ММП при нормальном распределении признаков совпадают с МНК. • трёхшаговый метод наименьших квадратов (для всех форм моделей, более эффективен для оценивания параметров рекурсивной модели) - на первом шаге к исходной модели применяется обобщенный метод наименьших квадратов - затем к полученным уравнениям применяется двухшаговый метод наименьших квадратов. ОМНК – обобщенный метод наименьших квадратов (метод Эйткена) • Применяется к эконометрической модели, которой свойственна гетероскедастичность. • Заключается в корректировки модели (замена переменных). • Предполагается, что среднее остатков равно нулю, а их дисперсия пропорциональна величинам ki (ki - коэффициенты пропорциональности) • Вводятся новые переменные и получают новое уравнение в преобразованных переменных, в котором уже остатки будут гомоскедастичны. • новые переменные — это взвешенные исходные переменные. • Экономически значимые примеры систем одновременных уравнений Статическая модель Кейнса (Кейнсианская модель формирования доходов) • • • • С - личное потребление в постоянных целях Y - национальный доход I - инвестиции в постоянных ценах - случайная составляющая C a bY Y C I • Эта модель точно идентифицируема, и для оценки параметров применяется КМНК • приведенная форма модели: a b 1 C 1 b 1 b I 1 b Y a 1 I 1 1 b 1 b 1 b Статическая модель Кейнса с функцией сбережения • r – сбережения C a bY 1 r T K (C I ) 2 Y C I r