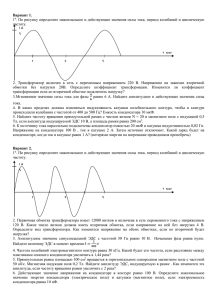
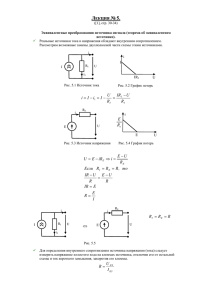
Задача 491 f C I
реклама

Задача 491 В сеть переменного тока частотой f = 50 Гц и напряжением U = 220 В включены последовательно конденсатор C = 10 мкФ и резистор R = 100 Ом. Используя метод комплексных амплитуд (см. раздел.15.2), рассчитайте действующие значения тока I, напряжения на конденсаторе Uc и напряжения на резисторе UR . Дано: f 50 Гц , U 220 B , C 10 мкФ 10 7 Ф , R 100 Ом Найти: I Д , UC Д , U R Д – ? Решение Согласно методу комплексных амплитуд запишем второе правило Кирхгофа: U C U R U . (1) Здесь комплекс напряжения равен: U U . (2) Учтем связь комплексов напряжений и токов на элементах: j I U C , U R I R . C (3) Тогда получим для комплекса тока в цепи: j I j C I R U I R U . U I C C R C j (4) Отсюда выразим модуль комплекса тока и рассчитаем действующее значение силы тока: I C 2 R j C U U U . 2 R C j R C 1 R C 2 1 C R C 2 1 C U U 2 R C 1 R C 2 1 C I Д I 2 f C 2 f R C 2 1 U 2 50 10 7 2 50 100 10 7 2 1 220 6.9 10 3 A . Выразим комплекс напряжения на конденсаторе и найдем действующее напряжение на нем: j I j C j 1 j R C U C U U U . C C R C j R C j R C 2 1 UC Д R C 2 1 U U 2 R C 1 R C 2 1 220 2 50 100 10 7 2 1 219.9 В Выразим комплекс напряжения на резисторе и найдем действующее напряжение на нем: U R I R URД R C R C j U R C R C j U R C 2 1 R C R C 2 1 U R C 2 1 R C U R C 2 1 2 50 100 10 7 220 2 50 100 10 7 2 1 0.69 В . Ответ: действующее значение тока равно: I Д 6.9 10 3 A , действующее значение напряжения на конденсаторе равно: U C Д 219.9 В , напряжения на резисторе равно: U R Д 0.69 В . действующее значение