a Vektor - Сайт школы 307 | school307.uz
реклама
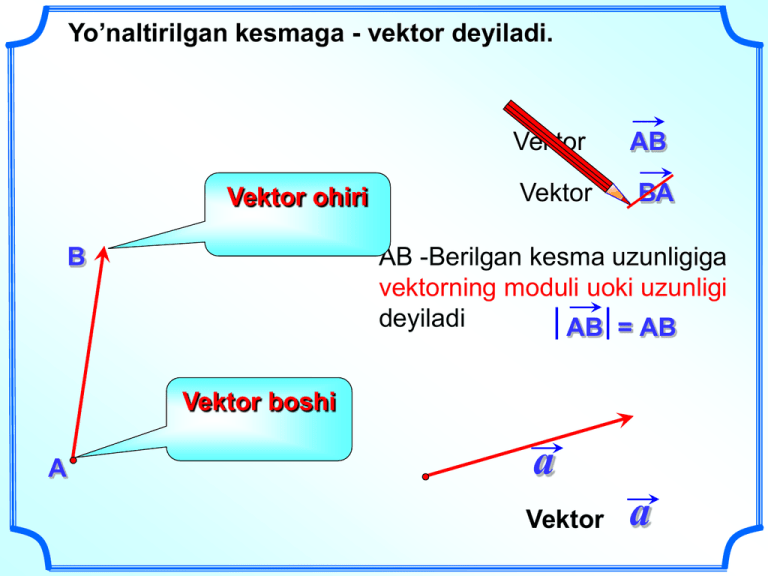
Yo’naltirilgan kesmaga - vektor deyiladi. Vektor ohiri В Vektor АВ Vektor ВА АВ -Berilgan kesma uzunligiga vektorning moduli uoki uzunligi deyiladi АВ = АВ Vektor boshi А a Vektor a Rasmda ko’rsatilgan vektorlarning boshi va oxirini ayting Vektor ЕF vektor AB Vektor CD Vektor NN F A E C В N D yoki 0 Многие физические величины, например сила, перемещение материальной точки, скорость, характеризуются не только своим числовым значением, но и направлением в пространстве. Такие физические величины называются векторными величинами (или коротко векторами) A 1Н 8Н В При изучении электрических и магнитных явлений появляются новые примеры векторных величин. E + Электрическое поле, создаваемое в пространстве зарядами, характеризуется в каждой точке пространства вектором напряженности электрического поля. На рисунке изображены векторы напряженности электрического поля положительного точечного заряда. Направление тока B Электрический ток, т.е. направленное движение зарядов, создает в пространстве магнитное поле, которое характеризуется в каждой точке пространства вектором магнитной индукции. На рисунке изображены векторы магнитной индукции магнитного поля прямого проводника с током. Kolleniar ,bir hil yo’nalgan vektorlar c b a a b c b c a Nul vektor istalgan yo’nalishdosh vektor bilan kolleniar hisoblanadi. o a o c o b Agar ikki nulga teng bo’lmagan vektorlar bir to’g’ri chiziqda yoki parallel to’g’ti chiziqlarda yotsa bunday vektorlar kolleniar vektorlar deyiladi Kolleniar, qarama qarshi yo’nalgan vektorlar b a c a b c b Uzunliklari teng va yo’nalishdosh bo’lgan vektorlarga o’zaro teng vektorlar deyiladi В a 2 a С О А 1 b = b D АВСD – parallelogramm. ВA = CD; AВ = DC; CВ = DA; Qolgan teng vektorlarni toping. О – nuqta diogonallar kesishmasi . AD = BC. a Agar А nuqta –vektor boshi bo’lsa boshlab qo’yilgan deyiladi vektor A nuqtadan a Istalgan nuqtadan berilgan vektor uzunligiga teng bo’lgan yagona vektor o’lchab qo’yish mumkin a ac А a Vektor М c A nuqtadan qo’yilgan a = c a a=c Отложить вектор, равный a n 1 от точки М М a c 2 от точки D D № 745 В прямоугольнике АВСD АВ=3см, ВС=4см, точка М – середина стороны АВ. Найдите длины векторов. АВ = 3 В 4 С ВC = 4 DС = 3 MА = 1,5 3 M 5 СВ = 4 АС = 5 А D МC = № 747 Укажите пары коллинеарных (сонаправленных) векторов, которые определяются сторонами параллелограмма MNPQ. P N M MN Q QP NM PQ QM PN MQ NP № 747 Укажите пары коллинеарных (противоположно направленных) векторов, которые определяются сторонами параллелограмма MNPQ. P N M MN Q PQ NM QP MQ PN QM NP № 747 Укажите пары коллинеарных (сонаправленных) векторов, которые определяются сторонами трапеции АВСD с основаниями AD и BC. В С А СВ D DA ВС AD Сонаправленные векторы ВС DA СВ AD Противоположно направленные векторы № 747 Укажите пары коллинеарных векторов, которые определяются сторонами треугольника FGH. G F Коллинеарных векторов нет H № 748 В параллелограмме АВСD диагонали пересекаются в точке О. Равны ли векторы. Обоснуйте ответ. С В О А AВ = DC; D ВС = DА; AО = ОC; AС = ВD. АВСD – квадрат, АВ = 4. Заполните пропуски: В 4 С 1. АВ и CD – … 2. ВС … СD, так как … 4 А О 3. АО = … D 4. ВО = АО, так как … 5. СО = СА, так как … 6. DD … , DD = … АВСD – параллелограмм. По данным рисунка найти АВ = 12 С В 12 300 А 6 К D АВС – равнобедренный треугольник. О – точка пересечения медиан. По данным рисунка найти DO = 2 В ВO = 4 10 O 6 А 2 8 D 16 С № 746 АВСD – прямоугольная трапеция. Решение Найти ВD , CD , AC Из АВD : B BD 122 52 169 13 C Из КСD : 5 5 СD 52 52 50 5 2 450 A К 7 12 7 D Из АВС : АС 52 7 2 25 49 74 № 749 Точки S и Т являются серединами боковых сторон MN и LK равнобедренной трапеции MNLK. Равны ли векторы. NL = KL; N S L MS = SN; MN = KL; T TS = KM; M K TL = KT. В четырехугольнике АВСD АВ = DC , О – точка 10 Если вдиагоналей. четырехугольнике сторонычерез точку m проходит пересечения Прямая две и параллельны, этот четырехугольник – О и равны пересекает стороны ВС ито АD в точках МиN параллелограмм. соответственно. ! ?! АВ DC и АВ ВС , АВСD – параллелограмм Среди векторов В M С ВМ, МС, АN, DN, AM, NC найдите Проверка а) коллинеарные ВМ, МС, АN, DN; векторы; AM и NC; О б) сонаправленные ВМ МС АN; векторы; АМ NС; в) противоположные DN МС; DN AN; векторы; DN BM; А N m D MC = AN; AM = NC; г) равные векторы; д) векторы, равные BM = DNимеющие ; MC = AN ; AMдлины. = NC . Vektor haqida tushuncha. • 8- sinflar uchun . • Matematika o’qituvchisi: Abdullayeva T.R.