Построение плана ускорений рычажных
реклама
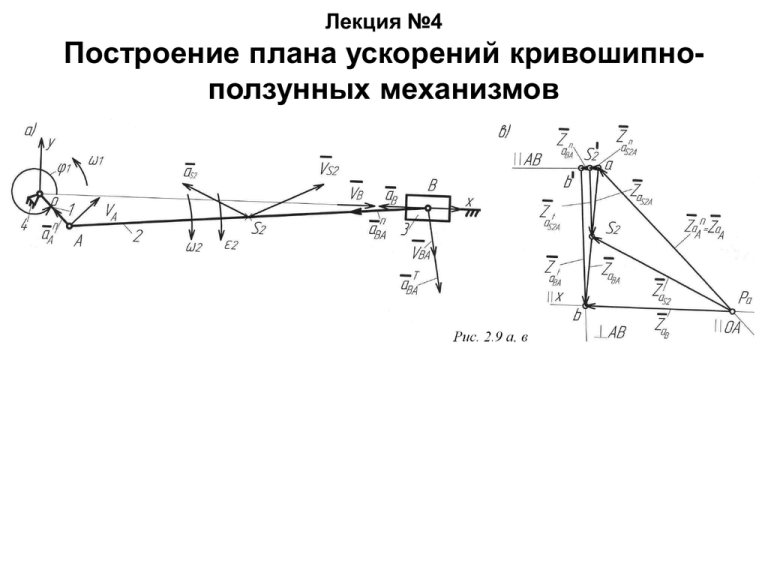
Лекция №4 Построение плана ускорений кривошипноползунных механизмов Векторное уравнение для построения плана ускорений Построение плана ускорений позволяет определить линейные ускорения точек А, В и S2 , а также угловое ускорение звена 2. n Ускорение точки А кривошипа складывается из суммы нормальной a A и тангенциальной t a A составляющих n t aA aA aA, (2.42) где a A 11 ; a A 11. 0, если 1 const . Ускорение точки В, принадлежащей звену 2, можно представить в виде векторной суммы ускорений переносного и относительного движений (2.43) a B a Bе a Br , где a Bе a A ; a Br a BA . Относительное ускорение точки В также состоит из двух составляющих n t a BA a BA a BA , (2.44) t n 2 где aBA 22 ; a BA 2 2 . n 2 t d 1 1 0 окончательно получим С учетом приведенных выше формул и в случае dt n n t (2.45) a B a A a BA a BA . // х // OA // AB BA Построение плана ускорений Построение плана ускорений начинаем с выбора масштабного коэффициента плана n ускорений K a по любой известной величине – либо по a An , либо по aВA . Пусть n a (2.46) K a An , ZaA где Z a An - длина отрезка, изображающего ускорение a An . an n n n Тогда величина отрезка Z a BA , изображающего известное ускорение aBA , будет Z aBA BA . Ka t t aBA Ka ZaBA и aB K a Z aB . Так как вектор ускорения a B направлен в сторону отрицательной полуоси х, то знак ускорения a B будет отрицательным. Соединив прямой точки а и b плана ускорений, получим отрезок aв , изображающий полное относительное ускорение a BA . Его величина будет aBA Ka aв. Величина углового ускорения звена 2 определяется из уравнения t aBA 2 , 2 0. (2.47) 2 Ускорение точки S 2 определяется из векторного уравнения n (2.48) a S 2 a A a S 2 A. // OA // a BA Величина относительного ускорения aS 2 A находится аналогично скорости S2 A - методом пропорционального деления отрезка ab, изображающего относительное ускорение aBA (2.49) AS AS a S 2 A a BA 2 или на рис. 2.9, в a S 2 аb 2 . AB AB Полное ускорение точки определяется как aS 2 ZaS 2 K a . S2 Графоаналитический метод кинематического анализа механизма с гидроцилиндром План положений План положений механизма для заданного значения обобщенной координаты 21 показан на рис. 2.10, а. По известным длинам звеньев AB , 3 BC , 4 AC и углу 4 определяются угловые положения звеньев 1-2 и 3 1 и 3. На рисунке точка S3 является центром тяжести звена 3, положение которого определяется углом и длиной CS3 , а точки Sц и Sn - центры тяжести соответственно цилиндра и поршня со штоком. План положений построен в соответствии с масштабным коэффициентом K , определенным по длине какого-либо звена механизма. План механизма с гидроцилиндром План скоростей позволит определить угловые скорости звеньев 1-2 и 3, линейные скорости центров тяжести всех звеньев по заданным кинематической схеме механизма, построенной в масштабе (рис. 2.10, а) и закону движения начального звена, например 21 const . Абсолютная скорость B2точки, принадлежащей звену 2, равна геометрической сумме переносной Bе и относительной Br скоростей этой точки B2 Bе Br . (2.50) При определении переносной скорости точки предполагается, что относительное движение точки остановлено. Переносной скоростью точки В звена 2 является движение со скоростью точки В, принадлежащей звену 1 B1 , а относительной скоростью является поступательное движение звена 2 относительно звена 1, т.е. Bе B1 и Br 21. B3 B1 21. С учетом равенства B2 B3 векторное уравнение скоростей будет иметь вид BC AB // AB (2.51) Данное векторное уравнение решается, поскольку оно имеет не более двух неизвестных – определению подлежат модули абсолютных скоростей точек B1 и B 3 B1 и B3 . Масштабный коэффициент плана скоростей K 21 . Z21 Z ; B3 K ZB3 . Неизвестные скорости определяются как B1 K B1 B1 B3 Угловые скорости звеньев 1 и 3 равны 1 ; 3 , 1 0,3 0 AB 3 (2.53) Линейные скорости центров тяжести звеньев Линейная скорость центра тяжести цилиндра Sц (звено 1) как точки, лежащей на звене АВ, находится методом пропорционального деления отрезка p в1, изображающего скорость B1: AS ZSц ZB1 ц AB . Sn Линейная скорость центра тяжести поршня (звено 2), совершающего сложное движение, определяется, как и для точки , суммированием переносной и относительной скоростей Sn Sne Snr или Sn Sn 1 21, (2.54) АВ АВ где Sn 1 - вектор скорости точки, принадлежащей цилиндру и лежащей на расстоянии ASn от точки А, определяется аналогично скорости точки центра тяжести цилиндра S ц . Численные значения скоростей равны Sц К ZSц ; Sn К ZSn . Вектор линейной скорости центра тяжести третьего звена S3 направлен перпендикулярно линии CS3 в соответствии со знаком угловой скорости .Величина скорости определяется как 3 . S3 lcs 3 3 Векторное уравнение для построения плана ускорения механизма с гидроцилиндром. План ускорений механизма с гидроцилиндром позволяет определить угловые ускорения звеньев 1-2 и 3, а также линейные ускорения центров тяжести всех звеньев. При составлении уравнения ускорений следует учитывать, что абсолютное ускорение a B 2 точки В, принадлежащей второму звену, складывается из геометрической суммы трех ускорений – переносного вместе с первым звеном a Bе , относительного a Br и кориолисова ускорения a K , которое появляется в том случае, если переносное движение оказывается вращательным: n t (2.55) a B 2 an Bе at Br a K a Bе a Bе a Br a K , где a Bе и a Bе - соответственно нормальное ускорение точки В в переносном вращательном движении, направленное по радиусу вращения точки к центру вращения А, и касательное ускорение, направленное перпендикулярно радиусу вращения. n n 2 t t При этом aBе aB1 1 AB ; aBе aB1 1 AB ; aBr a21 0, т.к.21 const; aK 2е r 21 21. Направление кориолисова ускорения определяется поворотом в плоскости чертежа относительной скорости 21 в направлении переносной угловой скорости 1 на 90 . Для положительной скорости 21 направление a K будет Если учесть, что a B 2 a B3 a B3 a B3 , aBn 3 32 3 ,aBt 3 3 3 , n t то окончательно уравнение плана ускорений будет иметь вид n t n t a B 3 a B 3 a B1 a B1 a K . // BC BC // AB AB AB (2.56) План ускорений механизма с гидроцилиндром Графическое решение уравнения плана ускорений Графическое решение уравнения состоит в определении неизвестных касательных составляющих линейных ускорений a Bt 1 и a Bt 3 . Масштабный коэффициент плана ускорений K a можно назначить, исходя из наибольшего известного значения ускорения. Пусть aBn 3 (2.57) Ka , n Z aB3 где Z aBn 3 - отрезок, изображающий ускорение a Bn 3 на плане ускорений. Тогда отрезки, пропорциональные значениям остальных известных определятся как: n ускорений, aB1 a ; ZaK K . Ka Ka aBt 1 K a ZaBt 1; aBt 3 ZaBt 3 . Z aBn1 Угловые ускорения звеньев 1-2 и 3 равны aBt 3 aBt 1 1 ; 2 . AB 3 (2.58) 3 Для определения знака углового ускорения следует перенести касательную t составляющую ускорения a B 3 из плана ускорений в точку В механизма. Действие ускорения по часовой стрелке определяет его отрицательный знак (рис. 2.10, а). Аналогично определяется направление ускорения 1 0. Линейные ускорения центров тяжести звеньев Линейное ускорение центра тяжести S3 звена 3 определяется уравнением n (2.59) t aS3 aS3 aS3, // CS 3 CS 3 где aS 3 3 CS 3 ; aS 3 3 CS 3 . Ускорение центра тяжести Sц цилиндра 1 определяется методом пропорционального деления отрезка в1в2 , изображающего абсолютное ускорение точки B1 , принадлежащей цилиндру AS AS (2.60) a Sц а В1 ц Z aSц Z aB1 ц . АВ или АВ Ускорение центра тяжести Sц поршня со штоком определяется уравнением (2.61) a Sn a Sn1 a K , n 2 t // в1// в 2 АВ где a Sn1 - ускорение точки цилиндра 1, располагающейся в точке Sn , и определяется аналогично ускорению aSц AS n (2.62) a Sn1 a B1 AB или Z aSn1 Z aB1 AS n . AB Для наглядности ускорения точек Sц и S n показаны на рис. 2.10, г, который является фрагментом плана ускорений и изображен не в масштабе. Действительные значения ускорений центров тяжести звеньев определяются уравнениями aS 3 K a Z aS 3 ; aSц K a Z aSц ; aSn K a Z aSn .








