Производная. МБОУ «Средняя школа № 3» Тетуева Г.Э. Высшая кв. категория
реклама

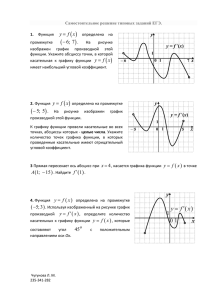
Производная. МБОУ «Средняя школа № 3» Тетуева Г.Э. Высшая кв. категория Найдите производные функций: 2 x 3x 1 4 3 15x 8х 3 2 Правильный 8x 9 x ответ 3 Правильный 60 xответ 8 1 Правильный 15 ответ 5х 2cos x Правильный 10 х 2sin x ответ 1 Правильный 6 хответ 2 х 4 15х x 2 1 2 3х х 2 x Найдите производные функций: 17 2 x 3x 1 2tg 3x Правильный 2 ответ 3 Правильный 2 3ответ x 1 6 Правильный 2 cosответ 3x 2sin x cos 3 x 3 ctg 5 x Правильный 2 cos x 3sin 3 x ответ 15 Правильный 2 sin 5x ответ Геометрический смысл производной Определите по графику функции у = f (x): у 1. Чему равен угловой коэффициент касательной в точке М? -1 0 2. Чему равна производная в точке М ? -1 0 М 3/4 3/4 подсказк а 1 135о а 0 М 1 М b х Функция y=f(x) задана на интервале (a;b), на рисунке изображен график ее производной. У прямых, параллельных К всех графику функции прямой y = 3 + x, угловой провели все коэффициент равен 1. касательные, параллельные прямой Поэтому y = 3 + xнайдём, (или сколько раз производная принимает совпадающие с ней). значение, равное 1. Найдите количество Для этого найдём число точек пересечения графика функции, точек графика в которых проведены производной с прямойэти y=1 касательные. Таких точек ровно 5. решение Ответ: 5 у y f (x) у=1 1 а 0 1 bх Функция y=f(x) задана на интервале (a;b), на рисунке изображен график ее производной. Найдем Найдитеугловой количество точек графика функции в a: коэффициент k = tg которых tg 135o = касательные -1. Найдём, сколько наклонены под углом 135о раз производная принимает к положительному значение, равное -1. направлению оси абсцисс. Для этого найдём число точек пересечения а графика производной с прямой y = -1 Таких точек ровно 5. решение Ответ: 5 у y f (x) 1 b 0 х 1 у = -1 Функция y=f(x) задана на интервале (a;b), на рисунке изображен график ее производной. у всех прямых, параллельных КУ графику функции провели прямой y = 4 -2x, угловой все касательные, коэффициент равен -2. параллельные прямой у в каких абсциссах с =Найдём, 4 - 2х (или совпадающие производная принимает ней). Найдите наибольшую значение, равное -2. из точек абсцисс, в которых Для этого найдём точки проведены эти касательные. пересечения графика производной с прямой y = -2 и выберем точку с наибольшей абсциссой. Это х=4. решение Ответ: 4 y f (x) 1 а 0 1 у = -2 4b х Функция y=f(x) задана на интервале (a;b), на рисунке изображен график ее производной. Найдем Найдитеугловой количество точек графика функции в a: коэффициент k = tg которых tg 60o = 3касательные . Найдём, сколько наклонены под углом 60о к раз производная принимает положительному значение, равное 3 . направлению оси абсцисс. Для этого найдём число точек пересечения а графика производной с прямой y = 3 Таких точек ровно 2. решение Ответ: 2 у 1 0 1 b х y f (x) Механический смысл производной ЗАДАЧА №1 Материальная точка движется прямолинейно по закону s (t) = 1 - 6t + 2,5t 2 Определить скорость через 2 с. после движения. РЕШЕНИЕ. v(t ) S (t ) 1)V1 (t ) (2,5t 2 6t 1) 5t 6 (формула скорости движения 1 тела) подсказк а Ответ: 4 ЗАДАЧА №2 Пусть количество вещества, вступившего в химическую реакцию задается зависимостью р( t ) = t 2/2 + 3t –3 (моль) Найти скорость химической реакции через 3 секунды. РЕШЕНИЕ. 1) v( t ) = p`( t ) = t + 3, v(t ) Р(t ) 2) v(3) = p`(3) = 3 + 3 = 6(моль/сек) подсказк а Ответ: 6 моль / сек Признаки возрастания и убывания функции Справочные сведения: Функция y = f(x) задана на интервале (a;b), на рисунке изображен график ее производной. у 1. Укажите промежутки убывания функции. y f (x) а;2, 3; b 2. Укажите промежутки возрастания функции. 2;3 3. Определите длину промежутка возрастания функции. 5 а 1 0 b 1 х Функция y = f(x) задана на интервале (a;b), на рисунке изображен график ее производной. у 1. Укажите промежутки убывания функции. y f (x) 3;3 2. Укажите промежутки возрастания функции. 1 a;3, 3; b 3. Определите длину промежутка, на котором касательная к графику функции имеет отрицательный угловой коэффициент? а 6 0 b 1 х Функция y = f(x) задана на интервале (a;b), на рисунке изображен график ее производной. у 1. Укажите промежутки убывания функции. y f (x) а;3, 0;3 2. Укажите промежутки возрастания функции. 3;0, 3; b 3. Определите длину наибольшего промежутка, на котором касательная к графику функции имеет положительный угловой коэффициент? 3 а 1 0 b 1 х Экстремумы функции Функция y=f(x) задана на интервале (a;b), на рисунке изображен график ее производной. у y f (x) 1. Назовите точки максимумов функции. х=0 2. Назовите точки минимумов функции. х = -3; х = 2 1 а b 0 1 х Функция y=f(x) задана на полуинтервале (a;b], на рисунке изображен график ее производной. у 1. Назовите точки максимумов функции. y f (x) х = -3, х = 2 2. Назовите точки минимумов функции. х = 1, х = 3 1 а 0 1 b х Функция y=f(x) задана на полуинтервале (a;b], на рисунке изображен график ее производной. 1. Верно ли, что отмеченные точки являются точками максимумов функции? у y f (x) нет 2. Назовите точки максимумов функции. х=0 3. Верно ли, что отмеченные точки являются точками минимумов функции? 1 а 1 0 bх нет 4. Назовите точки минимумов функции. х = -4, х = 4 5. Как называются оставшиеся точки? точки перегиба х = -2, х = 2 Определение свойств функции по графику её производной Информация , которую можно получить о функции y = f (x), если задан график её производной Функция убывает на промежутках: (а;-4], [-3;0],[1;2],[3;b] Функция возрастает на промежутках: [-4;-3],[0;1],[2;3] Точки экстремума: х = -4; х = -3; х = 0; х = 1; х = 2; х = 3 Точки максимума: х = -3; х = 1; х = 3 Точки минимума: х = -4; х = 0; х = 2 у f ( x ) 0 1 а 1 b х 0 f ( x ) 0 Функция y = f (x) задана на интервале (a;b), на рисунке изображен график ее производной. 1. В скольких точках касательная к графику функции параллельна оси абсцисс? 5 2. Сколько промежутков возрастания у функции? у f ( x ) 0 3 3. Назовите точки максимума. а х = -3 ; 3 4. Назовите точки минимума. х = 1; 4 5. Как называется точка х = -1? Точка перегиба. 1 0 f x 0 1 b х Найдите функцию по графику её производной у у 1 0 1 у 1 х 1 0 2 х 1 у 1 0 х 1 1 0 3 х 1 4 Задача 1. На рисунке изображен график y=f’(x) — производной функции y=f(x) , определенной на интервале (-8;3) В какой точке отрезка [-3;2] функция принимает наибольшее значение. Верно! y=f’(x) 1 -3 Подумай! 1 1 2 0 + Подумай! 3 3 Подумай! 4 1 ПРОВЕРКА (4) -3 - Задача 2. На рисунке изображен график y=f’(x) — производной функции y=f(x) , определенной на интервале (-8;4) В какой точке отрезка [-7;-3] функция принимает наибольшее значение. Подумай 1 y=f’(x) 1 Подумай 2 -2 + Подумай 3 - -5 Верно! 4 нет ПРОВЕРКА(3) Задача 3. На рисунке изображен график y=f’(x) — производной функции y=f(x) , определенной на интервале (-11;11) Найдите количество точек экстремума функции y=f(x), принадлежащих отрезку [-10;10]. 1 4 2 6 Подумай! y=f’(x) Подумай! + 3 5 4 7 Верно! - min + max - Подумай! ПРОВЕРКА (2) min max + - min Задача 4. На рисунке изображен график y=f’(x) — производной функции y=f(x) , определенной на интервале (-2;12) Найдите промежутки убывания функции y=f(x). В ответе укажите длину наибольшего из них. 1 2 2 4 3 6 4 8 Подумай! 6 Подумай! Верно! Подумай! ПРОВЕРКА (3) Задача 5. На рисунке изображен график y=f’(x) — производной функции y=f(x) , определенной на интервале (-10;2) Найдите количество точек , в которых касательная к графику функции y=f(x) параллельна прямой y= - 2x-11 или совпадает с ней. Верно! 1 5 Подумай! 1 2 4 3 3 1 Подумай! f‘(x)=-2 4 2 Подумай! ПРОВЕРКА(2) Задача 6. На рисунке изображен график y=f’(x) — производной функции y=f(x) , определенной на интервале (-4;8) Найдите точку экстремума функции y=f(x). Принадлежащей отрезку [-2;6]. Верно! 1 4 Подумай! 1 1 2 0 + Подумай! 3 3 Подумай! 4 -1 ПРОВЕРКА (1) max Задача 7. На рисунке изображен график y=f(x) и касательная к нему в точке x0. Найдите значение производной функции y=f(x) в точке x0. Подумай 1 2 1 tg 0,25 8 4 -1 Подумай 2 1 Подумай 3 8 0,5 Верно! 4 2 α 0,25 ПРОВЕРКА (5) Задача 8. На рисунке изображен график y=f(x) и касательная к нему в точке x0. Найдите значение производной функции y=f(x) в точке x0. 8 1 tg 2, значит,tg 0,5 4 2 1 2 Подумай! α Верно! 2 -0,5 β Подумай! 3 0,5 Подумай! 4 -2 ПРОВЕРКА (3) Задача 9. На рисунке изображен график функции y=f(x). Прямая, проходящая через начало координат , касается графика функции в точке с абсциссой 8. Найдите значение производной функции в точке x0 = 8. f '( x0 ) f '(8) tg 1 0,4 2 0,8 3 1,25 Подумай! Подумай! Верно! α 4 1 Подумай! ПРОВЕРКА (3) 10 1,25 8 Задача 10. На рисунке изображен график y=f’(x) — производной функции y=f(x) , определенной на интервале Найдите абсциссу точки , в которой касательная к графику y=f(x) параллельна прямой y= 2x-2 или совпадает с ней. Подумай 1 1 Подумай 2 0 Подумай 3 f’(x)=2 7 Верно! 4 5 5 ПРОВЕРКА (2) Задача 11. На рисунке изображен график функции y=f(x), определенной на интервале (-5;5) Найдите количество точек, в которых производная функции y=f(x) равна 0. 1 5 Подумай! y=f(x) Верно! 2 4 Подумай! 3 3 Подумай! 4 2 ПРОВЕРКА (3) Задача 12. Прямая y=5x-8 является касательной к графику функции f(x)=28x2 +bx+15. Найдите b, учитывая, что абсцисса точки касания больше 0. f ' ( x0 ) 5, 1 161 14 2 561 14 3 23 28 4 161 7 Верно! Подумай! 1 значит ,56 x0 b 5; b 5 56 x0 ; Т.к. парабола и касательная имеют общую точку с координатами x0 и y0 ,то составим уравнение: 28 x0 (5 56 x0 ) x0 15 5 x0 8 2 Подумай! Решим данное уравнение: 23 28 x 23; x ; 28 2 0 Подумай! x0 ПРОВЕРКА (7) 2 0 23 161 0; 28 14 Задача 13. 1 Материальная точка движется прямолинейно по закону x(t ) t 3 3t 2 2 2 где x –расстояние от точки отсчета в метрах, t-время в секундах измеренное с начала движения. Найдите скорость в м/с в момент времени t=6 c. 1 10 2 12 3 18 4 36 Подумай! v x' ( t ) Подумай! 3 2 x' ( t ) t 6t 2 Верно! 3 v x' (6) 36 6 6 54 36 18 2 Подумай! ПРОВЕРКА (3) Задача 13. 1 Материальная точка движется прямолинейно по закону x(t ) t 3 3t 2 2 2 где x –расстояние от точки отсчета в метрах, t-время в секундах измеренное с начала движения. Найдите скорость в м/с в момент времени t=6 c. 1 10 2 12 3 18 4 36 Подумай! v x' ( t ) Подумай! 3 2 x' ( t ) t 6t 2 Верно! 3 v x' (6) 36 6 6 54 36 18 2 Подумай! ПРОВЕРКА (3) Задача 14. Материальная точка движется прямолинейно по закону x(t ) t 2 13t 23 где x –расстояние от точки отсчета в метрах, t-время в секундах измеренное с начала движения. В какой момент вре мени (в секундах) ее скорость была равна 3 м/с? Подумай 1 11 Подумай 2 x' ( t ) 2t 13 Составим уравнение: 10 Подумай 3 v x' ( t ) 2t 13 3; t 8; 7 Верно! 4 8 2t 16; ПРОВЕРКА (5) Ответы к заданиям №1--- 1 №2-- - 4 №3---- 3 №4---- 3 №5---- 1 №6---- 1 №7--- 4 №8--- 4 №9---- 3 №10--- 4 №11----2 №12--- 1 №13----3 №14----8 Дом.зад. на карточках.