Двугранный угол

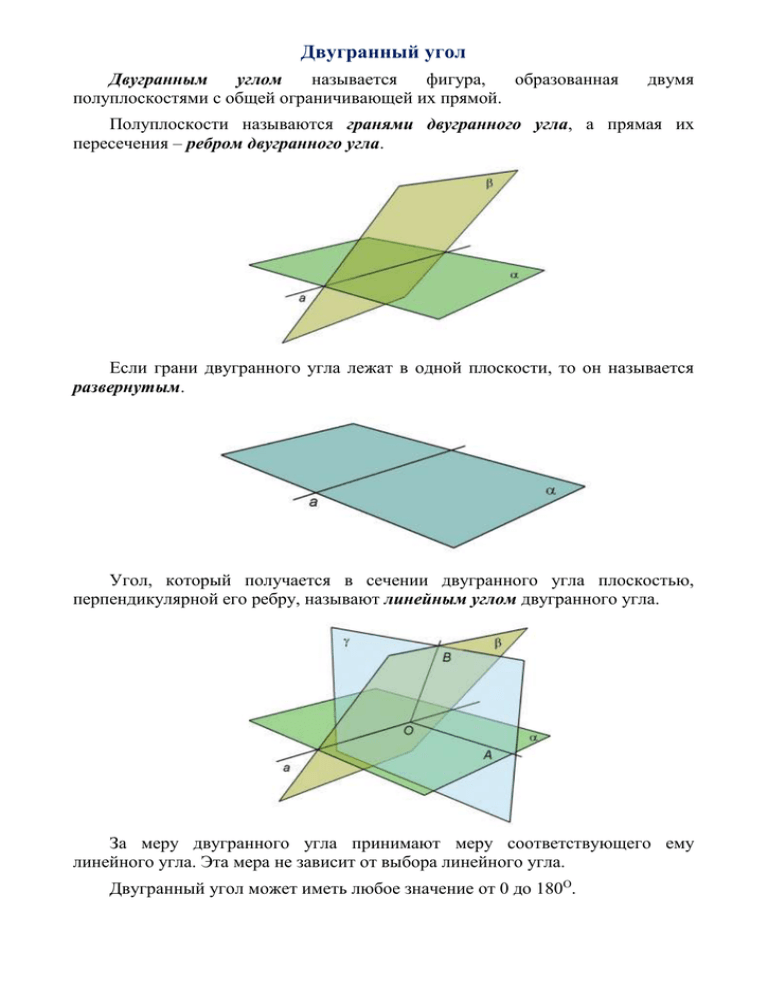
Двугранный угол
Двугранным
углом
называется
фигура,
образованная
полуплоскостями с общей ограничивающей их прямой.
двумя
Полуплоскости называются гранями двугранного угла, а прямая их
пересечения – ребром двугранного угла.
Если грани двугранного угла лежат в одной плоскости, то он называется
развернутым.
Угол, который получается в сечении двугранного угла плоскостью,
перпендикулярной его ребру, называют линейным углом двугранного угла.
За меру двугранного угла принимают меру соответствующего ему
линейного угла. Эта мера не зависит от выбора линейного угла.
Двугранный угол может иметь любое значение от 0 до 180О.
Двугранный угол называется прямым, если его градусная мера равна 90О.
О
Двугранный угол называется острым, если его градусная мера меньше
90 .
Двугранный угол называется тупым, если его градусная мера больше 90О.
Углом между плоскостями называется угол между прямыми,
перпендикулярными линии пересечения плоскостей, проведенных через
некоторую точку.
Пусть  и  – заданные плоскости, пересекающиеся по прямой а.
Через некоторую точку О прямой а проведем в плоскости  прямую ОАа,
а в плоскости  – прямую ОВа. Угол между прямыми ОА и ОВ – это угол
между плоскостями  и .
За угол между плоскостями принимают меньший из двух неравных между
собой двугранных углов, образуемых полуплоскостями этих плоскостей. Угол
между плоскостями всегда не больше 90О.
Градусная мера угла между параллельными плоскостями считается равной
нулю.
Примеры решения задач
Задача № 1. Пусть А и В – точки на ребре двугранного угла, АС и BD –
перпендикуляры к ребру, проведенные в разных гранях. Определить
двугранный угол, если АВ=24 см, АС=8 см, BD=5 см, а расстояние между
точками С и D равно 25 см.
Дано: АВ=24 см, АС=8 см, BD=5 см,
CD=25 см.
Найти: САК
Решение:
Проведем прямые АКBD и DKAB. Так как АВАС и АВАК, то АВ(САК).
Значит, и КD(САК), отсюда KDСК.
Из прямоугольного треугольника CKD, где угол К=90о, по теореме Пифагора
найдем КС= CD2  KD2 =7 см.
Так как (САК) АВ, то угол САК – линейный угол двугранного угла.
По теореме косинусов из треугольника САК найдем: cos(CAK)=(АС2+АК2КС2)/(2АКАС)=1/2. Значит, линейный угол, а, следовательно, и двугранный,
равен 60о.
Ответ: 60о
Задача № 2. Концы отрезка АВ лежат на гранях двугранного угла,
равного 60о. Из точек А и В проведены перпендикуляры AD и ВС к ребру
двугранного угла. Вычислите длину отрезка CD, если АВ=25 см, AD=8 см и
ВС=5 см.
Дано: АВ=25 см, AD=8 см, ВС=5 см,
ADO=60о
Найти: КО
Решение:
Пусть  и  - грани двугранного угла, ребро которого l, отрезок АО –
перпендикуляр, проведенный из точки А к грани . Так как АО, то отрезок
AD является наклонной к , а DO – ее перпендикулярная проекция на .
Так как ADl, то DOl (если прямая перпендикулярна наклонной, то она
перпендикулярна ее проекции). Таким образом, ADO – линейный угол
данного двугранного угла, т.е ADO=60о.
В треугольнике ADO DO=AO/2=4 см, АО= AD2  DO 2 =4 3 см.
Пусть ОКl, тогда DC=OK. В треугольнике ОКВ (ОКВ=90о) длина катета
ОК= OB 2  KB2 .
В треугольнике АОВ (АОВ=90о, АО=4 3 см, АВ=25 см) длина катета ОВ=
AB2  AO2 = 577 см.
Таким образом, в треугольнике ОКВ (ОКВ=90о, КВ=ВС-СК=ВС-DO=1 см)
КО= OB 2  KB2 =24 см.
Ответ: 24 см
Задача № 3. Через основание равнобедренного треугольника АВС
проведена плоскость α. Расстояние от точки А до плоскости α равно 4 см.
Вычислите градусную меру двугранного угла ABCO (точка О – основание
перпендикуляра, опущенного из точки А на плоскость α), если ВС=12 см,
АВ=АС=10 см.
Дано: ВС=12 см, АВ=АС=10 см,
АО=4 см.
Найти: AFO
Решение:
Пусть точка F – середина стороны ВС. Тогда AF – медиана равнобедренного
треугольника АВС, проведенная к его основанию. Следовательно, AFВС.
Отрезок OF является проекцией наклонной AF на плоскость , значит OFВС.
Так как AFВС и OFВС, то AFO линейный угол двугранного угла АВСО.
В треугольнике AOF (AOF=90o, АО=4 см) sinAFO=AO/AF.
В треугольнике AFC (AFC=90o, FC=BC/2=6 см, АС=10 см) длина катета АF=
AC 2  FC 2 =8 см.
Таким образом, sinAFO=AO/AF=1/2, AFO=30о.
Ответ: 30о
Задача № 4. Вычислите градусную меру двугранного угла при основании
правильной четырехугольной пирамида TABCD, боковая грань и диагональное
сечение которой равновелики.
Дано: TABCD – пирамида,
STDC=SATC
Найти: ОFТ
Решение:
Пусть О=АСBD, а точка F – середина отрезка DC. Тогда OFD – линейный
угол двугранного угла TDCO (так как ОFDC, TFDC). В треугольнике ТОF
(ТОF=90о) sinOFT=OT/TF.
Пусть DC=а, тогда АС=а 2 , SATC=ACTO/2, STDC=DCTF/2. По условию задачи
SATC=STDC. Следовательно, ТО/ТF= 2 /2, т.е. sinOFT= 2 /2, OFT=45о.
Ответ: 45о
Задача № 5. Основание прямой призмы АВСА1В1С1 – треугольник АВС,
в котором АВ=ВС=7 см, АС=2 см. Через прямую АС проведена плоскость α
под углом 30о к плоскости АВС, пересекающая боковое ребро ВВ1 в точке D.
Найдите площадь полученного сечения.
Дано: АВСА1В1С1 – призма, АСα,
(α, АВС)=30о, АВ=ВС=7 см, АС=2
см
Найти: SADC
Решение:
В треугольнике ADC сторона АС=2 см. Для нахождения его площади
необходимо найти высоту, проведенную к стороне АС.
DB(АВС) (так как призма прямая, то DBFD и DBBC). Кроме того, CD=AD
(наклонные, имеющие равные проекции СВ и АВ).
Пусть О – середина отрезка АС, тогда медиана OD – высота равнобедренного
треугольника ADC, а DОB=30o (так как DOAC и ВОАС).
В треугольнике ВОС катет ВО= ВC 2 ОC 2 =4 3 см.
В треугольнике ODB (OBD=90o, DOB=30o, BO=4 3 см) гипотенуза
OD=OB/cos30o=8 см.
Теперь находим SADC=ACOD/2= 8 см2.
Ответ: 8 см2
Задания для самостоятельной работы
Вариант 1
1. Градусная мера угла между параллельными плоскостями считается равной…
1) 180о
2) 90о
3) 0о
2. Дана правильная треугольная призма. Чему равен угол между плоскостями
(АВС) и (ВСС1)…
1) 0о
2) 45о
3) 60о
4) 90о
3. Если одна из двух плоскостей проходит через прямую, перпендикулярную
другой плоскости, то эти плоскости…
1) Параллельны;
2) Перпендикулярны;
3) Пересекаются под углом
4. ABCDA1B1C1D1 – куб. Чему равен угол между плоскостями (АВС) и (АСС1)?
5. ABCDA1B1C1D1 – куб. Найдите градусную меру двугранного угла D1CBA.
6. Найдите угол между двумя плоскостями, если точка А лежащая в одной из
этих плоскостей, отстоит от второй плоскости на расстоянии 4 см, а расстояние
от этой точки до прямой пересечения плоскостей равно 8 см.
7. Катет ВС прямоугольного треугольника АВС (АВС=90о) лежит в плоскости
α. Точка О – основание перпендикуляра, проведенного из вершины А к
плоскости α. Двугранный угол ABCO равен 45о. Вычислите градусную меру
угла между прямой АС и плоскостью α, если ВС=2 см, АО= 2 см.
8. Точки А и В лежат на ребре двугранного угла, АС и BD – перпендикулярны к
ребру, проведенные в разных гранях. Вычислите двугранный угол, если АВ=24
см, АС=8 см, BD=5 см и расстояние между точками С и D равно 25 см.
9. Ребро CD тетраэдра ABCD перпендикулярно к плоскости ABC,
AB=BC=AC=6 см, BD = 3 7 см. Найдите двугранный угол DACB.
10. АВСА1В1С1 – правильная треугольная призма. Вычислите боковую
поверхность призмы, если двугранный угол В1АСВ равен 60о, а площадь
сечения призмы плоскостью АСВ1 равна 8 3 см2.
Вариант 2
1. Двугранный угол называется острым, если его градусная мера…
1) Больше 90о
2) Равна 90o
3) Меньше 90о
2. Дан куб ABCDA1B1C1D1. Чему равен угол между плоскостями (АВС) и
(А1В1С1)…
1) 0о
2) 45о
3) 60о
4) 90о
3. Прямая, проведенная в одной из двух перпендикулярных плоскостей
перпендикулярно прямой, по которой они пересекаются…
1) Параллельна другой плоскости;
2) Пересекает другую плоскость под углом;
3) Перпендикулярна другой плоскости
4. ABCA1B1C1 – правильная треугольная призма. Чему равен угол между
плоскостями (ВСС1) и (АСС1)?
5. ABCDA1B1C1D1 – прямоугольный параллелепипед. Найдите меру
двугранного угла ВАСС1, если АС=2ВС.
6. В основании прямой треугольной призмы АВСА1В1С1 лежит
равнобедренный треугольник АВС (АВ=ВС). Найдите угол между плоскостями
(АВВ1) и (В1ВС), если АС=8 см, ВС=4 2 см.
7. В треугольнике АВС АВ=8 см, АС=6 см, ВС=10 см. Через сторону АС
проходит плоскость α, которая образует с плоскостью треугольника
двугранный угол 60о. Вычислите длину проекции стороны АВ на плоскость α.
8. Точка О – средина ребра ВВ1 прямой треугольной призмы АВСА1В1С1.
Площадь сечения призмы плоскостью АСО равна 4 3 см2. Найдите градусную
меру двугранного угла, если АС=3 см, ВС=4 см, АСВ=90о.
9. Дан куб ABCDA1B1C1D1. Найдите двугранный угол АВВ1С.
10. Основанием пирамиды служит ромб, длина стороны которого равна 6 см, а
острый угол – 30о. Двугранный угол при ребре основания равен 60о. Вычислите
боковую поверхность пирамиды.
Вариант 3
1. Плоскость, перпендикулярная к ребру двугранного угла, пересекает его грани
по…
1) Прямой
2) Полупрямой
3) Двум полупрямым
2. Дан прямоугольный параллелепипед ABCDA1B1C1D1. Чему равен угол между
плоскостями (АВС) и (DCС1)…
1) 0о
2) 45о
3) 60о
4) 90о
3. Прямая, проведенная в плоскости и перпендикулярная наклонной…
1) Перпендикулярна и ее проекции на эту плоскость
2) Параллельна и ее проекции на эту плоскость
3) Перпендикулярна плоскости
4. ABCDEFA1B1C1D1E1F1 – правильная шестиугольная призма. Чему равен угол
между плоскостями (ВСС1) и (FЕЕ1)?
5. ABCA1B1C1 – правильная треугольная призма. Найдите градусную меру
двугранного угла ВСС1D1.
6. Дан прямоугольный параллелепипед ABCDA1B1C1D1. Вычислите градусную
меру двугранного угла А1СDА, если CD=4 см, AD=2 2 см.
7. В кубе ABCDA1B1C1D1 точки Т и К – середины ребер СС1 и DC
соответственно. Найдите угол между плоскостями ATD и A1D1K.
8. АВСА1В1С1 – правильная треугольная призма. Вычислите боковую
поверхность призмы, если двугранный угол В1АСВ равен 60о, а площадь
сечения призмы плоскостью АСВ1 равна 8 3 см2.
9. Ребро CD тетраэдра ABCD перпендикулярно к плоскости ABC,
AB=BC=AC=6 см, BD = 3 7 см. Найдите двугранный угол DABC.
10. В правильной треугольной призме через сторону нижнего основания и
середину противолежащего ребра проведена плоскость, образующая с
плоскостью основания двугранный угол 60о. Площадь сечения равна 8 3 см2.
Вычислите площадь боковой поверхности призмы.
Вариант 4
1. Если грани двугранного угла лежат в одной плоскости, то он называется…
1) Тупым; 2) Развернутым; 3) Острым
2. Дана правильная шестиугольная призма ABCDEFA1B1C1D1E1F1. Чему равен
угол между плоскостями (АВВ1) и (ВСС1)…
1) 60о
2) 90о
3) 120о
4) 180о
3. Прямая, проведенная в плоскости и перпендикулярная проекции наклонной
на эту плоскость…
1) Параллельна плоскости;
2) Перпендикулярна плоскости;
3) Перпендикулярна наклонной
4. ABCDA1B1C1D1 – прямоугольный параллелепипед. Чему равен угол между
плоскостями (АВВ1) и (АСС1), если АС=2ВС?
5. ABCDA1B1C1D1 – куб. Найдите градусную меру двугранного угла А1CBA.
6. В основании прямоугольного параллелепипеда ABCDA1B1C1D1 лежит ромб,
диагонали которого BD=6 см и АС=6 3 см. Найдите величину двугранного
угла ACDD1.
7. Основание прямого параллелепипеда ABCDA1B1C1D1 – параллелограмм
ABCD, площадь которого 40 см2. Вычислите площадь сечения параллелепипеда
плоскостью ADB1, если известно, что она образует с плоскостью основания
угол 60о.
8. В правильной треугольной призме через сторону нижнего основания и
середину противолежащего ребра проведена плоскость, образующая с
плоскостью основания двугранный угол 60о. площадь сечения равна 8 3 см2.
Вычислите площадь боковой поверхности призмы.
9. Ребро CD тетраэдра ABCD перпендикулярно к плоскости ABC,
AB=BC=AC=6 см, BD = 3 7 см. Найдите двугранный угол BDCA.
10. В правильной треугольной призме АВСА1В1С1 точка О – середина отрезка,
соединяющего центры оснований. Найдите градусную меру угла наклона
плоскости АОС к плоскости основания, если все ребра призмы равны между
собой.
Вариант 5
1. Двугранный угол равен…
1) Его линейному углу
2) Углу между двумя перпендикулярами, проведенному к линии
пересечения плоскостей
3) Углу между двумя пересекающимися прямыми, лежащими в разных
плоскостях
2. Дана правильная четырехугольная призма ABCDA1B1C1D1. Чему равен угол
между плоскостями (ADD1) и (АВВ1)…
1) 0о
2) 45о
3) 60о
4) 90о
3. Через любую точку пространства можно провести…
1) Сколько угодно плоскостей, параллельных данной плоскости
2) Две плоскости, параллельных данной плоскости
3) Только одну плоскость, параллельную данной плоскости
4. ABCDA1B1C1D1 – прямой параллелепипед, в основании которого лежит
ромб, угол ВАD=60о. Чему равен угол между плоскостями (АВВ1) и (ВВ1С1)?
5. ABCDA1B1C1D1 – прямоугольный параллелепипед в основании которого
лежит ромб. Найдите градусную меру двугранного угла АОВВ1, где точка О –
точка пересечения диагоналей основания.
6. В основании прямоугольного параллелепипеда ABCDA1B1C1D1 лежит ромб,
диагонали которого BD=6 см и АС=6 3 см. Найдите величину двугранного
угла ACDD1.
7. Точки К и М – середины ребер SC и АС тетраэдра SABC соответственно.
Найдите угол между плоскостями АВК и SBM.
8. Основанием пирамиды служит ромб со стороной 6 см и острым углом 30 о.
двугранный угол при ребре основания равен 60о. вычислите боковую
поверхность пирамиды.
9. Дан куб ABCDA1B1C1D1. Найдите двугранный угол АDD1B.
10. Основание прямого параллелепипеда ABCDA1B1C1D1 – ромб с углом 30о
при вершине А. Вычислите площадь сечения, проходящего через сторону DC и
середину ребра ВВ1, если длина стороны ромба равна 10 см, а сечение
наклонено к плоскости основания под углом 60о.
Вариант 6
1. Двугранным углом называется фигура…
1) Образованная двумя полуплоскостями с общей ограничивающей их
прямой
2) Образованная двумя плоскостями с общей прямой
3) Образованная двумя полуплоскостями
2. Дана правильная треугольная призма ABCA1B1C1. Чему равен угол между
плоскостями (АВВ1) и (ВВ1С1) …
1) 0о
2) 45о
3) 60о
4) 90о
3. Если две плоскости параллельны третьей, то они…
1) Пересекаются; 2) Параллельны; 3) Перпендикулярны
4. ABCDA1B1C1D1 – прямоугольный параллелепипед, в основании которого
лежит квадрат. АА1=2АВ. Чему равен угол между плоскостями (АВС) и (АВК),
где точка К – середина стороны СС1?
5. ABCA1B1C1 – правильная треугольная призма. Найдите градусную меру
двугранного угла АВВ1С1.
6. АВСА1В1С1 – правильная треугольная призма. Найдите величину
двугранного угла ОВСС1, где точка О – середина стороны АС.
7. Основание треугольной пирамиды DABC – прямоугольный треугольник
АСВ с прямым углом при вершине С, DA(ABC). Вычислите градусную меру
двугранного угла ABCD, если АС=ВС=1 см, DB= 5 см.
8. В правильной треугольной призме АВСА1В1С1 точка О – середина отрезка,
соединяющего центры оснований. Вычислите градусную меру угла наклона
плоскости АОС к плоскости основания, если все ребра призмы равны между
собой.
9. Найдите двугранный угол ABCD тетраэдра ABCD, если углы DAB, DAC и
АСВ прямые, АС=СВ=5 см, DB=5 5 см.
10. Основанием пирамиды является равнобедренный треугольник, боковые
стороны которого равны 2 см и образуют угол 30 о. Двугранные углы при всех
сторонах основания равны 60о. Найдите площадь полной поверхности
пирамиды.
Вариант 7
1. Двугранный угол называется тупым, если его градусная мера…
1) Больше 90о
2) Равна 90o
3) Меньше 90о
2. Дан прямоугольный параллелепипед ABCDA1B1C1D1. Чему равен угол между
плоскостями (АВВ1) и (DCС1)…
1) 0о
2) 45о
3) 60о
4) 90о
3. Если две плоскости перпендикулярны прямой, то они…
1) Перпендикулярны
2) Параллельны
3) Скрещиваются
4. ABCA1B1C1 – правильная треугольная призма. Чему равен угол между
плоскостями (АВВ1) и (КВВ1), где точка К – середина стороны АС?
5. ABCDA1B1C1D1 – правильная четырехугольная призма. Найдите градусную
меру двугранного угла АВВ1D1.
6. В основании прямоугольного параллелепипеда ABCDA1B1C1D1 лежит ромб,
диагонали которого BD=6 см и АС=6 3 см. Найдите величину двугранного
угла BDCC1.
7. Сторона AD ромба ABCD лежит в плоскости α, образующей с плоскостью
ромба угол 60о. Вычислите длину стороны ромба, если ABD=45о, а
расстояние от вершины В ромба до плоскости α равно 3 см.
8. Основанием пирамиды является равнобедренный треугольник, боковые
стороны которого равны 4 см и образуют угол 30 о. Двугранные углы при всех
сторонах основания равны 60о. найдите площадь полной поверхности
пирамиды.
9. Найдите угол при ребре основания правильной четырехугольной пирамиды,
если высота пирамиды в два раза меньше стороны основания.
10. Плоскости α и β взаимно перпендикулярны и пересекаются по прямой а. Из
точки М проведены перпендикуляры МА и MB к этим плоскостям. Прямая а
пересекает плоскость АМВ в точке С. Найдите расстояние от точки М до
прямой а, если АМ=4 см, ВМ=3 см.
Вариант 8
1. Углом между плоскостями называется угол между прямыми…
1) Перпендикулярными линии пересечения плоскостей, проведенных
через некоторую точку
2) Перпендикулярными линии пересечения плоскостей, проведенных
через некоторую точку и лежащими в разных плоскостях
3) Параллельными линии пересечения плоскостей, проведенных через
некоторую точку
2. Дан куб ABCDA1B1C1D1. Чему равен угол между плоскостями (АВС) и
(АСС1)…
1) 0о
2) 45о
3) 60о
4) 90о
3. Отрезки параллельных прямых, расположенные между параллельными
плоскостями…
1) Перпендикулярны; 2) Равны; 3) Не равны
4. ABCDEFA1B1C1D1E1F1 – правильная шестиугольная призма. Чему равен угол
между плоскостями (АВВ1) и (EDD1)?
5. ABCDA1B1C1D1 – куб. Найдите градусную меру двугранного угла АВВ1D1.
6. Основание прямой призмы АВСА1В1С1 – прямоугольный треугольник АВС
(АВС=90о). Вычислите градусную меру двугранного угла С1АВС, если
ВС=СС1.
7. На ребре СС1 куба ABCDA1B1C1D1 взята точка К – середина этого ребра.
Найдите угол, который образует плоскость BDK с плоскостью АВ1С1.
8. Основание прямой призмы АВСАВС – равнобедренный прямоугольный
треугольник АВС (АВС=90о). Двугранный угол С1АВС равен 60о. Вычислите
площадь сечения призмы плоскостью АВС1, если АС=4 2 см.
9. В правильной пирамиде SABC боковое ребро в два раза больше стороны
основания. На ребре SC взята точка Р – такая, что секущая плоскость АВР
перпендикулярна прямой SC. Найдите величину двугранного угла ВАРС.
10. Проекцией прямоугольника ABCD на плоскость α является квадрат ABCD.
Вычислите угол между плоскостью α и плоскостью прямоугольника ABCD,
если АВ:ВС=1:2.
Вариант 9
1. Двугранный угол называется прямым, если его градусная мера…
1) Больше 90о
2) Равна 90o
3) Меньше 90о
2. Дана правильная четырехугольная пирамида TABCD. Чему равен угол между
плоскостями (АВС) и (АСТ)…
1) 30о
2) 45о
3) 60о
4) 90о
3. Если две параллельные плоскости пересечены третьей, то прямые их
пересечения…
1) Параллельны
2) Перпендикулярны
3) Скрещиваются
4. ABCDA1B1C1D1 – куб. Чему равен угол между плоскостями (АСС1) и
(ВDD1)?
5. ABCDA1B1C1D1 – прямоугольный параллелепипед. Найдите меру
двугранного угла ВСАА1, если АС=2ВС.
6. На ребрах АВ, ВС и MB правильного тетраэдра МАВС взяты соответственно
точки L, D и С - середины этих ребер. Найдите угол между плоскостью ABC и
плоскостью, проходящей через прямую LK параллельно прямой MD.
7. Найдите угол между плоскостями, если точка, взятая на одной из них,
отстоит от прямой пересечения плоскостей вдвое дальше, чем от второй
плоскости.
8. Боковое ребро правильной призмы АВСА1В1С1 равно стороне ее основания.
На ребре АА1 взяты точки К1, К2 и К3 – такие, что АК1=К1К2=К2К3=К3А1.
Найдите угол между плоскостью ВК2С и В1К2С1.
9. На ребрах АА1 и СС1 правильной призмы АВСА1В1С1 взяты соответственно
точки М и К – середины этих ребер. Угол между прямыми АВ1 и СМ равен 90о.
Найдите двугранный угол КАВС.
10. Два плоских угла трехгранного угла равны каждый по 45 о, а двугранный
угол между ними равен 90о. Найдите третий плоский угол этого трехгранного
угла.
Вариант 10
1. За меру двугранного угла принимается мера соответствующего ему….
1) Угла между двумя перпендикулярами к линии пересечения плоскостей
2) Линейного угла
3) Угла между двумя пересекающимися прямыми, лежащими в разных
плоскостях
2. Дана правильная шестиугольная пирамида SABCDEF. Чему равен угол
между плоскостями (SOD) и (SOC)…
1) 30о
2) 45о
3) 60о
4) 90о
3. Прямая, проведенная через точку одной из перпендикулярных плоскостей
перпендикулярно второй плоскости…
1) Пересекает первую плоскость
2) Не лежит в первой плоскости
3) Лежит в первой плоскости
4. ABCDA1B1C1D1 – прямоугольный параллелепипед. Чему равен угол между
плоскостями (АВС) и (А1В1С1)?
5. ABCDEFA1B1C1D1E1F1 – правильная шестиугольная призма. Найдите
градусную меру двугранного угла ВСDD1.
6. На ребре СС1 куба ABCDA1B1C1D1 взята точка К - середина этого ребра.
Найдите угол, который образует плоскость BDK с плоскостью CB1D1.
7. В треугольнике АВС АВ=8 см, АС=6 см, ВС=10 см. Через сторону АС
проходит плоскость α, которая образует с плоскостью треугольника
двугранный угол 60о. Вычислите длину проекции стороны АВ на плоскость α.
8. На ребрах АВ, ВС и SB правильного тетраэдра SABC взяты соответственно
точки М, D и К – середины этих ребер. Найдите угол между плоскостью АВС и
плоскостью, проходящей через прямую МК параллельно прямой SD.
9. Основание прямой призмы АВСА1В1С1 – прямоугольный треугольник АВС
(АВС=90о). Найдите градусную меру двугранного угла С1АВС, если ВС=СС1.
10. 10. Внутри трехгранного угла SPQR, каждый плоский угол которого равен
2α, через точку S – вершину угла – проведен луч SK, образующий равные углы
с ребрами трехгранного угла. Найдите двугранный угол PSKQ.
Ответы
Вариант
1
Вариант
2
Вариант
3
Вариант
4
Вариант
5
Вариант
6
Вариант
7
Вариант
8
Вариант
9
Вариант
10
1
3
3
3
2
1
1
1
2
2
2
2
4
1
4
3
4
3
1
2
4
3
3
2
3
1
3
3
2
2
2
1
3
4
45
60
0
30
60
45
30
0
90
0
5
45
60
30
90
90
60
45
90
60
60
6
30
90
45
30
30
30
60
45
90
90
7
30
4
90
80
60
60
2
30
30
4
8
60
30
72
144
36
60
12
16
60
90
9
90
90
45
60
45
60
45
90
30
45
10
72
36
144
60
100
3
5
60
60
120