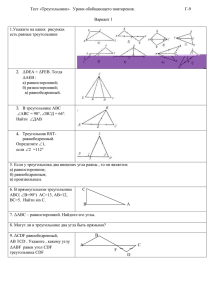
, BC = CD CM BCD
реклама
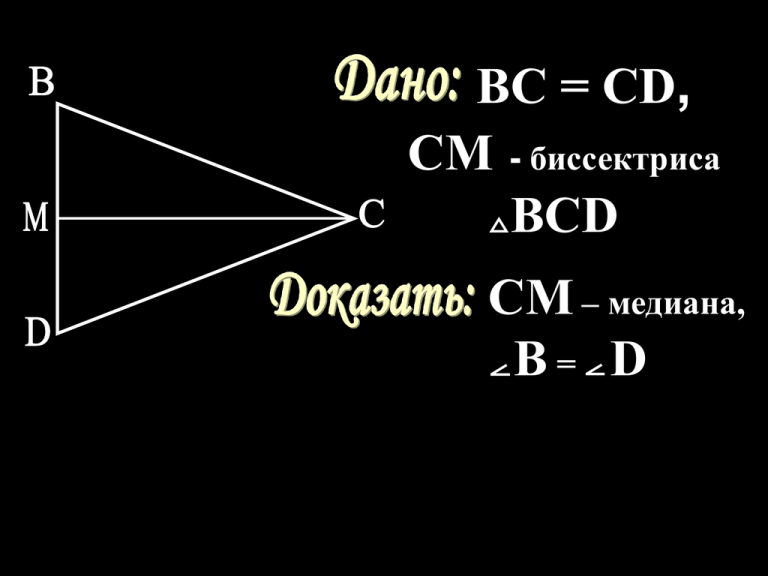
BC = CD, CM - биссектриса BCD CM – медиана, B= D 1 2 BC = CD, CM - биссектриса BCD CM – медиана, B= D B B C A C A AB ≠ BC ≠ AC Разносторонний B AB = BC Равнобедренный C A AB = BC = AC Равносторонний Виды треугольников относительно длин сторон: 1) разносторонний; 2) равнобедренный; 3) равносторонний. Равнобедренный треугольник D В P В M F K Рис. 1 А основание С Рис. 2 Назовите: боковые стороны; основание; углы, прилежащие к основанию; угол, противолежащий основанию. Равнобедренный треугольник В АВС – равнобедренный с основанием АС ИЛИ А С АВС, АВ = ВС В 1 2 3 С 70 0 50 0 45 0 0 70 0 50 45 0 1 В А В равнобедренном треугольнике боковая сторона равна 10 см и основание 8 см. В Найти периметр С треугольника. 3 В С А D 2 А В равностороннем треугольнике сторона равна 7 см. Вычислите С периметр треугольника. Равносторонний и равнобедренный треугольники имеют общее основание. Периметр равностороннего треугольника равен 36 см, а равнобедренного 40 см. Найти стороны данных треугольников. А Дано : ABC– равнобедренный, BC – основание, M Є BC, N Є BC, BM = NC. Доказать: BAM = CAN, AMN – равнобедренный. Решение В М N С 1. По условию АВС – равнобедренный с основанием ВС, значит, АВ = АС как боковые стороны, В = С как углы при основании. ВМ = NC - по условию. Следовательно, ВАМ = САN по Ι признаку равенства треугольников. 2. В равных треугольниках против равных углов лежат равные стороны, значит, АМ = АN. Следовательно, AMN – равнобедренный по определению.