«Многокритериальная оптимизация проектных решений
реклама

«Многокритериальная оптимизация
проектных решений методом
адаптивных взвешенных сумм»
Выполнил: Савелов А.С.
Руководитель: Карпенко А.П.
Задачи дипломного проекта
1) Выявить недостатки AWS-метода и предложить его модификации
2) Разработать программную систему для приближенного построения
множества Парето AWS-методом
3) Произвести исследование эффективности предложенных модификаций
AWS-метода
4) Решить практически значимые задачи построения множества Парето:
обратные задачи химической кинетики ДИБАГ и ДИБАХ
2
Постановка задачи МКО
min F ( X ) F ( X * ) F *
X DX
(1)
D X { X } R | X | - область допустимых значений
F ( X ) f1 ( X ), f 2 ( X ) - двухкритериальная вектор-функция
DF - множество достижимости
Необходимо построить аппроксимации множества и фронта Парето
X , F
Лицо, принимающее решение, из множеств
X , F должно выбрать
решение задачи (1)
Вектор F1 DF
неравенств
доминирует вектор F2 DF , если среди равенств и
f k ( X 1 ) f k ( X 2 ), k [1:| F |], имеется, хотя бы одно строгое
DF* DF - точки, для которых нет более предпочтительных точек
DF* - фронт Парето
DX* DX , соответствующее DF* DF , - множество Парето
3
Метод взвешенных сумм (WS-метод)
( X ) 1 f1 2 f 2 - взвешенная сумма критериев
min ( X ) ( X * ) *
X DX
(2)
начало
Покрытие множества D
сеткой
Выбор j
Решение задачи глобальной
оптимизации (2). Получение
X *j D *X и Fj* DF*
конец
Решение задачи min ( X ) C можно интерпретировать как поиск значения С,
X DX
при котором прямая ( X ) C будет касательной к множеству DF* задачи (1)
Теорема: выбор определенной точки из множества Парето эквивалентен
указанию весов для каждой из частных целевых функций
D { | 0 k 1, k [1: 2]} - множество допустимых значений вектора весов
4
Схема AWS-метода
Свободные параметры метода:
- начальный радиус
области доверия (ОД)
- коэффициент сужения ОД
min - минимальная величина
радиуса ОД
начало
Определение центральной точки
j * arg max d j | X j X T ,
j
Построение доверительной области DC
Формирование метамоделей критериев
m1 ( X ), m2 ( X )
Формирование взвешенных сумм
mp ( X ) 1p m1 ( X ) 2p m2 ( X )
mq ( X ) 1q m1 ( X ) q2 m2 ( X )
Решение оптимизационных задач
min m1 ( X ) m1 ( Xˆ 1 ), min m2 ( X ) m2 ( Xˆ 2 ),
X
T
c ( f ( X
X DC
X DC
X DC
min mp ( X ) mp ( Xˆ p ), min mq ( X ) mq ( Xˆ q )
- множество точек, которые не могут
быть приняты за центральные
DC { X | X D X , X X C }
X DC
) f ( X ))
p c p ( f 2 ( X C ) f 2 ( X j* 1 )), ( f1 ( X C ) f1 ( X j* 1 ))
q
q
2
)
j 1
f 2 ( X C )), ( f1 ( X j* 1
1
C
нет
X XT
да
конец
5
Построение метамоделей на основе квадратичной аппроксимации
целевых функций
0
x
1 j k
i i
1 j j k
ij xi x j ii xi2
x2
начало
1i k
x3
Формирование матрицы плана
X C
x1
0
x1
Схемы ЦКП: X 2 и X 3
Испытание критериальных
функций в точках
проектирования центрального
композиционного плана (ЦКП)
Нахождение коэффициентов
модели методом наименьших
квадратов
Ядро ЦКП
Полный
факторный
эксперимент
x2
Дробная
реплика
конец
6
Модификация 1 – на основе повышения разнообразия множества
архивных точек
Задача ZDT3 (двумерная,
двухкритериальная):
DX = X |0 xi 1,i [1: X ], X 10 ,
f1 X f ( x1 ) = x1 ,
f1 ( X ) f1 ( X )
1
g( X ) g( X ) ,
f2 X = g ( X )
sin 10 π f ( X )
1
X
xi
g ( X ) g x2 ,..., x X = 1 + 9
i = 2 X 1
X 1 и X 2 - крайние точки текущей
Парето-аппроксимации
0,25
.
Задача ZDT3: оригинальный AWS-метод
Задачи оптимизации:
min m1 ( X ),
min m1 ( X ),
min m2 ( X );
min m2 ( X );
X D1
X D1
X D2
X D2
D1 { X | X D X , X X 1 1},
D2 { X | X D X , X X 2 2 }.
Задача ZDT3: точный фронт Парето
7
Модификация 2 – на основе смещения области доверия
x2
DX
0
Задача ZDT3: множество Парето
DC
x1
Схема смещения области доверия
Смещаем центр области доверия «вглубь» области определения, не
изменяя при этом ее радиуса.
8
Модификация 3 – построение метамоделей на основе
нейросетевой аппроксимации целевых функций
x2
x3
начало
X C
x1
0
x1
x2
Схемы ЦКП: X 2 и X 3
Размещение центров
нейронов в точках
проектирования квадратичной
метамодели
Формирование обучающей
выборки
Обучение нейронной сети
(нахождение весов и ширин
нейронов)
Радиальный нейрон
yi wi exp(
X j Ci
2
i
конец
2
); j 1,2,..., N , i 1,2,..., L
9
Разработка программной системы
10
Тестовые задачи МКО
Задача Аудета:
D X = X | 0 xi 1, i 1, 2
Задача ZDT3:
f1 X = f1 (x 1 ) 4 x1
f1 X f ( x1 ) = x1 ,
f 2 X = g ( X ) h X
f1 ( X ) f1 ( X )
1
g
(
X
)
g
(
X
)
f2 X = g ( X )
,
sin 10 π f ( X )
1
α
f1 ( X )
, f1 ( X ) g ( X ),
1
h X =
g
(
X
)
0, иначе,
x 0,2 2
.
g X g ( x2 ) = 4 3 exp 2
0,02
DX = X |0 xi 1,i [1: X ], X 2 ,
g ( X ) g x2 ,..., x X
X
xi
= 1+ 9
i = 2 X 1
.
Задача ZDT7:
Задача ZDT6:
DX = X | 0 xi 1, i [1: X ], X 2
DX = X | 0 xi 1, i [1: X ], X 2
f1 X f ( x1 ) = 1 exp 4 x1 sin 6 6 π x1
f1 X f ( x1 ) = x1
f ( X ) 2
f 2 X = g ( X ) 1 1
g
(
X
)
0,25
X
xi
.
g ( X ) g x2 ,..., x X = 1 + 9
i = 2 X 1
0,25
X
g ( X ) g x2, ..., x X = 1 + 9
i= 2
h X = 1
f1 ( X )
.
g ( x2 ,..., x X )
xi
,
X 1
11
Индикаторы оценки производительности метода
Индикаторы качества Парето-аппроксимации
1) IONVG () max
- мощность множества решений
- архив решений
2) GD
3) SP
i 1
2
i
I ONVG ()
, i [1: ]
1
I ONVG 2
- близость найденных решений к точному
множеству Парето рассматриваемой МКОзадачи
1
2
(
s
s
)
i
i 1
- равномерность распределения
решений в полученной Паретоаппроксимации
Индикаторы эффективности
1) nE ( fi ) , i 1,2
- число испытаний целевых функций
12
Исследование эффективности - модификация 1
nE ( f1 )
450
nE ( f1 )
450
nE ( f 2 )
450
nE ( f 2 )
450
IONVG ()
33
IONVG ()
84
GD
0,087
GD
0,012
SP
0,122
SP
0,04
Задача Аудета: оригинальный AWS-метод
Задача ZDT3: оригинальный AWS-метод
nE ( f1 )
637
nE ( f1 )
494
nE ( f 2 )
637
nE ( f 2 )
494
IONVG ()
70
IONVG ()
90
GD
0,202
GD
0,011
SP
0,065
SP
0,04
Задача Аудета: AWS-метод (модификация 1)
Задача ZDT3: AWS-метод (модификация 1)
Исследование эффективности - модификация 2
Задача ZDT3: оригинальный AWS-метод
Задача ZDT3: AWS-метод (модификации 1 и 2), t 30
Задача ZDT3: AWS-метод (модификация 2)
Задача ZDT3: AWS-метод (модификации 1 и 2), t 100
Исследование эффективности - модификация 3
Задача ZDT3: квадратичная аппроксимация
nE ( f1 )
nE ( f 2 )
10314 10314
Задача ZDT7: квадратичная аппроксимация
IONVG ()
GD
SP
nE ( f1 )
nE ( f 2 )
IONVG ()
GD
SP
438
0,0007
0,017
9654
9654
133
0,001
0,015
Задача ZDT3: нейросетевая аппроксимация
nE ( f1 )
nE ( f 2 )
IONVG ()
GD
SP
35536
35536
91
0,005
0,046
Задача ZDT7: нейросетевая аппроксимация
nE ( f1 )
nE ( f 2 )
36384 36384
IONVG ()
GD
SP
388
0,0005
0,009
Однокритериальная обратная задача химической
кинетики (ДИБАГ)
Модель химической реакции:
dx1 dt k x k x k x x ,
( j)
( j) 2
( j)
( j)
dx2 dt 2k1 x1 2k2 x2 k3 x1 x3 k4 x2 x3 ,
( j)
( j)
dx3 dt k3 x1 x3 k4 x2 x3 ,
( j)
( j)
dx
dt
k
x
x
k
x2 x3 ,
4
3
1
3
4
X (0) X 0 .
( j)
1
1
( j) 2
2
2
xi - концентрации веществ; i [1: 4]
ki - константы скоростей стадий реакций
MXSE ( K ) max( xin xin )2 min,
i ,n
начало
( j)
3
1 3
i [1: 4], n 1: X
Решение СДУ,
получение вектора констант K
Вычисление функционала
MXSE
MXSE
да
нет
Корректировка K
xin , xin - расчетные и
экспериментальные значения
концентраций
конец
16
Двухкритериальная обратная задача химической
кинетики (ДИБАГ)
начало
Закон Аррениуса:
Решение СДУ
E
k k0 exp a ,
RT
E 1
ln k ln k0 a
R T
Вычисление функционала
MXSE
E a - энергия активации; T - температура;
R - газовая постоянная
Построение МНК-оценок констант
уравнения Аррениуса
Вычисление функционала
MLSE
MXSE ( K ) max( yin yin ) min,
2
i ,n
i [1: 4], n 1: X
MLSE ( K ) max
i, j
( j) 2
i
min,
i [1: 4], j [1: 3]
нет
Выполнен
критерий останова
метода МКО
да
конец
17
Двухкритериальная обратная задача химической
кинетики (ДИБАГ)
Задача ДИБАГ: фронт Парето
18
Двухкритериальная обратная задача химической
кинетики (ДИБАХ)
Модель химической реакции:
dx1 dt w4 w6 w10 ,
dx dt w 2w w w w w w ,
15
11
7
6
5
4
3
2
dx3 dt w5 w8 ,
dx4 dt w5 w8 w9 ,
dx dt w w w 2w w w w w ,
15
14
11
9
8
7
6
5
5
dx6 dt w9 w13 ,
dx dt w w w ,
12
11
9
7
dx8 dt w6 w7 w8 w10 ,
dx9 dt w1 w2 w3 w10 w12 w13 w15 ,
dx10 dt w2 w3 w10 w12 w14 w15 ,
dx11 dt w1 w3 w13 ,
dx dt w w ,
3
2
12
dx13 dt w1 w14 ,
dx14 dt w1 w2 ,
dx15 dt w13 ,
0
X (0) X ;
w1=k13x13x9-k18x14x11,
w2= k14x14x9,
w3= k8x10x9,
w4= k4x22- k1x1,
w5= k9x2x3,
w6= k2x1x5,
w7= k3x2x5,
w8= k12x8x3,
w9= k10x4x5,
w10= k6x1x9,
w11= k11x7x5,
w12= k15x7x9,
w13= k16x6x11-k19x15x9,
w14= k17x13x5-k20x10,
w15= k5x10x5-k7x2x9.
19
Двухкритериальная обратная задача химической
кинетики (ДИБАХ)
начало
Решение СДУ
Вычисление функционала
SSE
Определение индукционного
периода
Вычисление функционала
ITSE
max y(t ) y(tind )
t
tind
- индукционный период
нет
SSE ( K ) ( yn yn ) 2 , n 1: X
n
ITSE ( K ) (tind tind )2
Выполнен
критерий останова
метода МКО
да
конец
20
Двухкритериальная обратная задача химической
кинетики (ДИБАХ)
Задача ДИБАХ: фронт Парето
21
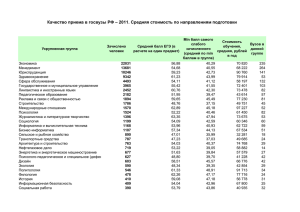
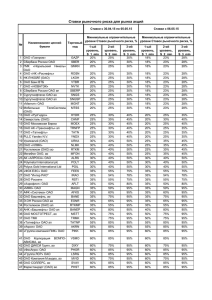
Организационно-экономическая часть
Диаграмма Ганта
№
п/п
Статьи затрат на НИОКР
Затраты,
руб.
Затраты, %
1
Фонд заработной платы
299904
72,9
2
Отчисления в фонды
89971
21,9
3
Амортизационные
отчисления
1041
0,3
4
Материальные затраты
20000
4,7
5
Прочие расходы
550
0,2
411466
100
Итого
Таблица затрат
Статьи затрат на НИОКР
22
Заключение
1) Выявлены недостатки AWS-метода и предложены его модификации
2) Разработана программная система для приближенного построения
множества Парето AWS-методом
3) Произведено исследование эффективности предложенных
модификаций AWS-метода
4) Решены практически значимые задачи построения множества Парето:
обратные задачи химической кинетики ДИБАГ и ДИБАХ.
5) Перспективы развития работы в проведении исследования
эффективности AWS-метода для числа параметров больше двух и
модификации метода для работы с числом критериев больше двух.
23
Спасибо
за внимание!