Лекция по МНК и ЗЛП
реклама
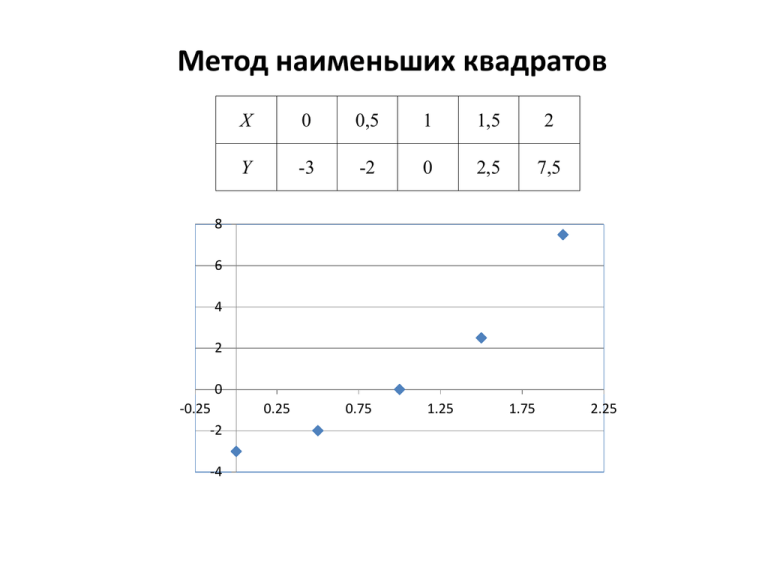
Метод наименьших квадратов X 0 0,5 1 1,5 2 Y -3 -2 0 2,5 7,5 8 6 4 2 0 -0.25 -2 -4 0.25 0.75 1.25 1.75 2.25 Необходимо построить функцию, которая бы проходила наиболее близко к указанным точкам y f x, a, b, c a bx cx 2 n n Q a, b, c yi y xi , a, b, c yi a bxi cxi2 i 1 i 1 xi , y i n 2 – координаты заданных точек (данные из таблицы) – количество заданных точек n xi x1 x2 x3 x4 ... xn1 xn i 1 2 n Q a, b, c yi i 1 a bxi cxi2 n дQ 2 yi a bxi cxi2 0, i 1 дa n дQ 2 yi a bxi cxi2 xi 0, i 1 дb n дQ 2 yi a bxi cxi2 xi2 0. дc i 1 n n n 2 an b xi c xi yi , i 1 i 1 i 1 n n n n 2 3 a xi b xi c xi y i xi , i 1 i 1 i 1 i 1 n n n n 2 3 4 a xi b xi c xi y i xi2 . i 1 i 1 i 1 i 1 2 X Y X2 0 -3 0 0,5 -2 0,25 1 0 1 1,5 2,5 2,25 2 7,5 4 Сумма 5 5 7,5 X3 0 0,125 1 3,375 8 12,5 X4 XY X2Y 0 0 0 0,063 -1 -0,5 1 0 0 5,063 3,75 5,625 16 15 30 22,13 17,75 35,13 Система уравнений для определения коэффициентов сглаживающей функции 5a 5b 7,5c 5, 5a 7,5b 12,5c 17, 75, 7,5a 12,5b 22,13c 35,13. Конечный вид сглаживающей функции y 2,886 0, 243 x 2, 429 x 2 8 6 y 2,886 0, 243 x 2, 429 x 2 4 2 0 -0.25 0.25 -2 -4 0.75 1.25 1.75 2.25 Задачи линейного программирования (оптимизация) Найти максимальное значение целевой функции F x1; x2 2 x1 5x2 max при следующих ограничениях x1 x2 127, 7 x1 x 2 83, x 0, x 0. 2 1 x1 , x2 – система ограничений – параметры оптимизации Построение математических моделей ЗЛП Задача планирования производства продукции Краска для – цена продажи 1 ед. 2 ден.ед. наружных работ А Потребление на 1 ед. Пигмент 1, т Олифа 2, т Склад Наименование Запас ресурса, ресурса т Пигмент 6 Олифа 12 Неизвестные параметры оптимизации Краска для – цена продажи 1 ед. 3 ден.ед. внутренних работ B Потребление на 1 ед. Пигмент 2, т Олифа 3, т x1 – количество краски А, ед. x2 – количество краски B, ед. Математическая модель F X F x1; x 2 2 x1 3x 2 max – целевая функция Пусть краски А требуется не более 4 ед. Система ограничений x1 2 x2 6, 2 x 3x 12, 1 2 x1 4, x1 , x2 0. – ограничение по запасам Пигмента – ограничение по запасам Олифы – ограничение по производству краски А – нельзя производить отрицательное кол-во краски Задача о составлении оптимального рациона Требуется в сутки Наименование Не менее чем Кормовые ед. 16,1 кг. 1816 г. Перевариваемый протеин Содержание питательных веществ в 1 кг корма и себестоимость кормов Показатель Комбикорм Сено Силос Кормовые единицы, кг Переваримый протеин, г 1 160 0,5 60 0,2 30 Себестоимость 1 кг корма, руб. 4,2 0,9 0,6 Согласно физиологическим особенностям животных в рационе должно содержаться не менее 31% комбикормов и не более 26% сена от общей потребности в кормовых единицах. . Математическая модель Целевая функция – общая стоимость суточного рациона кормления: F X 4, 2 x1 0,9 x 2 0, 6 x3 min Составим систему ограничений: 1) условие по содержанию кормовых единиц в рационе: x1 0,5x2 0, 2 x3 16,1 2) условие по содержанию перевариваемого протеина в рационе: 160 x1 60 x2 30 x3 1819 3) условие по содержанию комбикорма в рационе (не менее 31%) : x1 4,991 4) условие по содержанию сена в рационе (не более 26%) 0,5 x2 4,186 5) условие неотрицательности количества корма каждого вида: x1 0, x2 0, x3 0 Транспортная задача Цель – минимизация суммарных расходов на все перевозки Транспортная задача открытого типа 70 Математическая модель xij – количество перевозимой продукции от поставщика номер i к потребителю номер j X x11, x12 , x13 , x21, x22 , x23 , x31, x32 , x33 Целевая функция – общая стоимость всех перевозок: F X 5 x11 10 x12 12 x13 8 x 21 6 x 22 4 x 23 0 x31 0 x32 0 x33 min Общий вид целевой функции m n F X cij xij min i 1 j 1 c ij – элементы матрица стоимостей перевозок 5 C 8 0 10 6 0 12 4 0 Система ограничений ВЫВОЗ ПРОДУКЦИИ ОТ ПОСТАВЩИКА = ЗАПАСУ x11 x12 x13 120 Аналогично для остальных поставщиков: ПРИВОЗ ПРОДУКЦИИ К ПОТРЕБИТЕЛЮ = ПОТРЕБНОСТИ x11 x21 x31 60 Аналогично для остальных потребителей: x21 x22 x23 70 x12 x22 x32 100 x31 x32 x33 50 x13 x23 x33 80 Пример решения в MS EXCEL Постановка задачи Используемое сырьё Доски, м Обивочная ткань, м Рабочее время, чел./час Стоимость, руб. Расход сырья на изготовление одного изделия 1 типа 2 типа Кол-во сырья в распоряжении фабрики 2 0,5 2 80 4 0,25 2,5 120 440 65 320 max x1 – число изготовленных стульев x 2 – число изготовленных кресел F X 80 x1 120 x2 max – целевая функция прибыли Система ограничений 2 x1 4 x2 440, 2 x1 4 x2 440, 0,5 x 0, 25 x 65, 0,5 x 0, 25 x 65, 1 2 1 2 2 x1 2,5 x2 320, 2 x1 2,5 x2 320, x1 0, x2 0, x1 0, x2 0. Оформление страницы MS EXCEL Использование Надстройки «Поиск решения» Результаты решения в MS EXCEL









