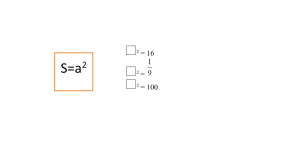
Квадратный корень из произведения

Знание - самое превосходное из владений.
Все стремятся к нему, само оно не приходит.
Абу-р-Райхан ал-Буруни.
Квадратный корень
из произведения
900igr.net
Повторим :
1. Как
называется выражение
а?
2. Что называется арифметическим
а?
квадратным корнем из числа
а выражение
3. При каком значении
а имеет смысл?
Найдите:
144 ; 225 ; 0
25; 16 ; 0,49

 
2
2
0,4 ; 15 ;  2 5
7

2
x  36 y  11
2
m  0 d 2  3
10
11
2
50
2
Сегодня мы
познакомимся еще с
одним из свойств
арифметического
квадратного корня.
Попробуем решить
Рассмотрим арифметический
корень
2 2
2
64 49





64

49

8

7

8

7

8

7

56
Найдите значение
64 49
выражения:
64
 49

8
7

56
Значит,
6449 64 49.
Итак, корень из произведения двух чисел равен
произведению корней из этих чисел.
Теорема
 Корень из
произведения
неотрицательных
множителей равен
произведению корней
из этих множителей.
Если
а0,в0, то
ав а в
Квадратный корень из произведения
Доказательство:
1. a  0и b  0, значит,
2.
3.
ab
a
4. Вывод:
 ab 0
 ab ab
ab , a , b - имеют смысл.
2
a 0
 a  a
b 0
b
2
 b  b
2
a b0,
(т.к. произведение двух неотрицательных чисел неотрицательно)
а

a


b
b
a

b
2
5. Итак,
2
2
ab
 a b
Мы рассмотрели
доказательство теоремы
об извлечении квадратного
корня из произведения.
Перейдём к
практической работе.
Сейчас я вам покажу как
применяется эта формула
при решении примеров.
Решайте вместе со мной.
Решаем примеры:
1. Вычислите значение квадратного корня, используя
теорему о корне из произведения:
 16

10
4

40
1) 100
16 100
4

12
2

24
2) 144
4 144
 81

5
9

45
3) 25
81 25
121
0
,
25

3

11

0
,
5

16
,
5
4
) 9
121
0
,25
9
25
0
,
36

20

5

0
,
6

60
5
) 400
25
0
,36
 400
Решаем примеры:
2. Найдите значение выражения:
1) 72
18 36

2

9

2

36

9

4

6

3

2

36

3

9

3

25

9

9

5

3

3

45
2) 75
27 25

0
,
1

25

0
,
1

36

25

0
,
01

6

5

0
,
1

3
3) 3,62,5 36

10

4

10

9

2

10

180
4) 810
40
 81
Быстрый счёт
А я догадался, как
можно использовать эту
формулу для быстрых
вычислений.
Смотри и учись.
16900 169
 100

13

10

130
1,96 
196
0
,
01

14
0
,
1

1
,
4
2
2



13

12
13

12

1

25

1

5

5
13
12
 
2
2



313

312
313

312

1

625

1

25

2
313
312
 
Предлагаю вам примеры для
самостоятельного решения:
Вариант 1
1. 25
8145
2.
3.
4.
16 36  24
4  0,36  1,2
10 * 250  50
2
2
5
. 104
40
96
Вариант 2
1. 121
6488
2.
36  49  42
3.
9  0,49  2,1
4.
160 90  120
2
2
5
. 117

108
45
Оцени себя сам:
№
заданий
1и 2
задания
1-3
задания
1-4
задания
Все
задания
отметка
3
4
5
5+
Чтобы вынести множитель из-под
знака квадратного корня, необходимо:
1. подкоренное число разложить на
множители таким образом, чтобы
хотя бы из одного множителя
можно было бы извлечь
квадратный корень (4; 9; 16; 25и
т.д.);
2. квадратный корень из произведения
записать как произведение квадратных
корней;
а в
2
ав а в
3. извлечь корень из тех множителей, из
которых он извлекается
а b  а b | a | b
2
2
2
2
Вынести множитель из под
знака корень
300  100  3  100  3  10 3
Чтобы внести множитель из-под
знака квадратного корня,
необходимо:
Выполнить цепочку преобразований в
обратном порядке
Вынесение множителя из под корня
аb а
2
2
b | a | b
Внесение множителя под коркнь
Внести множитель из под знака
корень
2 3  4 3  4  3  12
Упростить выражение
2 27  12  2 9  3  4  3  2 9 3  4 3 
 23 3  2 3  6 3  2 3 
Одинаковые корни складываются, как
подобные слагаемые:
Числа складываем, а неизвлекаемые корни
оставляем без изменения
6
32
3  (6  2)
3 8
3
Упростить выражение
b
a
b
a
2
2
3a
 2b
3 a
2 b

a
b
a
b
b
a
a b
b a
2
3 a  2 b  3
2

a
b
a
b
2
2
2
 3 ab  2 ab  (3  2) ab 
ab
Подведем итоги
 С какой теоремой мы сегодня
познакомились?
 Сформулируйте правило извлечения
квадратного корня из произведения?
 Когда пользуемся этим правилом?