ОЛИМПИАДА ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ «ОСЕНЬ-2010»
реклама
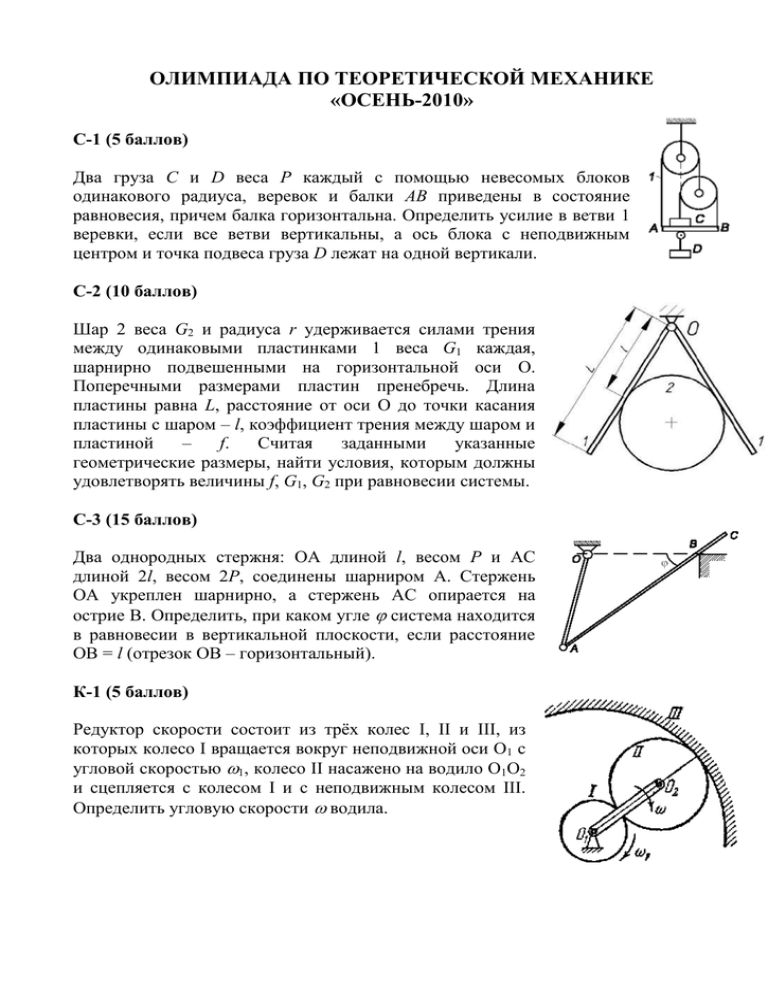
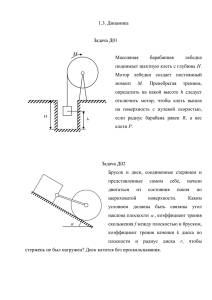
ОЛИМПИАДА ПО ТЕОРЕТИЧЕСКОЙ МЕХАНИКЕ «ОСЕНЬ-2010» С-1 (5 баллов) Два груза С и D веса Р каждый с помощью невесомых блоков одинакового радиуса, веревок и балки АВ приведены в состояние равновесия, причем балка горизонтальна. Определить усилие в ветви 1 веревки, если все ветви вертикальны, а ось блока с неподвижным центром и точка подвеса груза D лежат на одной вертикали. С-2 (10 баллов) Шар 2 веса G2 и радиуса r удерживается силами трения между одинаковыми пластинками 1 веса G1 каждая, шарнирно подвешенными на горизонтальной оси O. Поперечными размерами пластин пренебречь. Длина пластины равна L, расстояние от оси O до точки касания пластины с шаром – l, коэффициент трения между шаром и пластиной – f. Считая заданными указанные геометрические размеры, найти условия, которым должны удовлетворять величины f, G1, G2 при равновесии системы. С-3 (15 баллов) Два однородных стержня: ОА длиной l, весом Р и АС длиной 2l, весом 2Р, соединены шарниром А. Стержень ОА укреплен шарнирно, а стержень АС опирается на острие В. Определить, при каком угле система находится в равновесии в вертикальной плоскости, если расстояние ОВ = l (отрезок ОВ – горизонтальный). К-1 (5 баллов) Редуктор скорости состоит из трёх колес I, II и III, из которых колесо I вращается вокруг неподвижной оси О1 с угловой скоростью 1, колесо II насажено на водило О1О2 и сцепляется с колесом I и с неподвижным колесом III. Определить угловую скорости водила. К-2 (5 баллов) t3 Уравнения движения точки имеют вид: x ; y 2t 2 ; z 6 3 Определить ускорение точки в момент, когда скорость равна 15. К-3 (15 баллов) Прямая ОА вращается около точки О данной неподвижной окружности радиуса R с постоянной угловой скоростью . Определить скорость и ускорение точки М, в которой прямая ОА пересекает окружность. Д-1 (10 баллов) Сани весом Р скатываются с наклонной плоскости, образующей угол с горизонтом, причём начальная высота саней равна h. Найти расстояние х, которое они пройдут до остановки по горизонтальной плоскости, если коэффициент трения на всём пути одинаков и равен f. Д-2 (15 баллов) На однородный круглый цилиндр веса Р и радиуса R, который может вращаться вокруг горизонтальной оси, намотана цепь длиной l и весом G, несущая на конце груз веса Q. Определить закон вращения цилиндра под действием сил тяжести, если в начальный момент свешивалась длина x0 цепи и вся система находилась в покое. Силами сопротивления пренебречь. Д-3 (20 баллов) Центр шара радиуса r имеет скорость v0. Шар катится без проскальзывания по горизонтальной плоскости АВ, и переходит на наклонную плоскость, образующую с горизонтом угол . Какое наибольшее значение можно придать углу , чтобы при переходе на наклонную плоскость шар не оторвался от опоры?