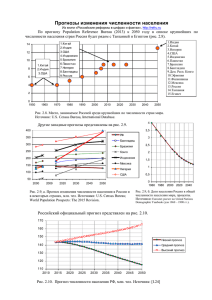
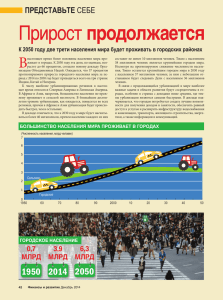
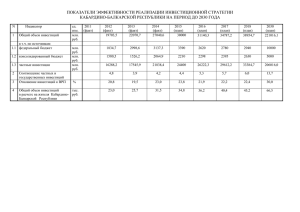
Сегментация Потребителей при Ценообразовании в

ПАРАЛЛЕЛЬНЫЕ ВЫЧИСЛЕНИЯ С
ИСПОЛЬЗОВАНИЕМ GRID-ТЕХНОЛОГИЙ В
МАТЕМАТИЧЕСКОМ МОДЕЛИРОВАНИИ
РЕГИОНАЛЬНОЙ ЭКОНОМИКИ
Н.Н. Оленёв, А.С. Стариков, А.В. Шатров
Вычислительный центр им. А.А. Дородницына РАН, Москва
Вятский государственный университет, Киров
olenev@ccas.ru, starikoff@gmail.com, avshatrov@yandex.ru
Содержание









Моделирование для оценки инновационного потенциала
Нормативная балансовая модель региональной экономики
Учет теневого оборота
Балансовое описание рынков продукции
Описание домашних хозяйств (агента L)
Проблема идентификации модели
Параллельные вычисления для оценки параметров
Проверка работоспособности модели
Сценарные численные эксперименты с моделью
Моделирование для оценки
инновационного потенциала






Для оценки инновационного потенциала надо сделать
анализ доступной статистики, структурировать данные и
сделать на основе этого анализа обоснованные выводы.
Можно исходить из имитационной модели.
Построение модели
Идентификация модели
Составление сценариев возможного развития
Численные эксперименты
Анализ численных экспериментов и модификация модели
Нормативная балансовая модель
экономики Кировской области
Экономические агенты в экономике Кировской области:
 X – сектор производства (лесопромышленный комплекс области),

Y - сектор производства (комплекс новых отраслей биотехнологии и
химии, наука, образование, инновационный),

Z - сектор производства (другие отрасли, включая сектор услуг),

L - домашние хозяйства,

T - торговый посредник,

B - региональная банковская система,

G - Правительство региона (консолидированный бюджет региона).
Правительство региона собирает налоги с производителей: налог на
прибыль n1, налог на добавленную стоимость n2, акцизы n3,
единый социальный налог n4, таможенные пошлины на экспорт n5,
- и домашних хозяйств: таможенные пошлины на импорт n6,
подоходный налог n7.
Учет теневого оборота
Произведенный продукт производители делят на легальный и
теневой, не облагаемый налогами, но штрафными санкциями.
Два вида денег – «белые» и «черные», которые могут отмываться.

  a
X
X L
L
YX  a Q
X
L
X
K

X
X K
K
Q
X  YX
Y
 (a Q )
X
Y
X  ZX
Z
 (a Q )
X
Z
dQXX
 1  q X YX  (a XXL  a XXY  a XXZ  a XXO )QXX  c XX I X
dt


dW X
 wpOX X XXO  C BX  p XL a XXL  pYX a XXY  p XZ a XXZ QXX 
dt
 bYXY  bZXZ  bWXY  bUXZ  bLXL  bHXB W X  T XG  T GX  bBX B X




dQVX
 q X YX  aVXL  aVXY  aVXZ QBX
dt
dB X
  pVL aVXL  pVY aVXY  pVZ aVXZ  QVX   bBXL  bBX  bBXG  B X
dt
Балансовое описание рынков продукции
Запас конечного продукта X лесопромышленного комплекса,
предназначенного агенту L (домашним хозяйствам) определяет
изменение индекса потребительских цен на продукцию X
LX
L
dQXL
b
W
 a XXLQXX  X L
dt
pX
LX
L

dp XL
b
W
L
XL X 
X
  X 
 a X QX 
L
dt
 pX

Описание домашних хозяйств (агента L)
Предложение труда и спрос на труд в открытой и теневой
частях секторов определяют изменение ставок зарплаты
dQLLX
bLXLW X
LX
LX
 a L QL 
dt
s LX
dQBLX
bBXL B X
LX
LX
 aB QB 
dt
sBX
dsLX  X  bLXLW X
 LX sLX
LX
LX 
  L 
 aL QL 
X
L
dt
s
p
L
X




 bXLX W L
XL X 


 a X QX  
L
p
X

 
dsBX  X  bBXL B X
 BX sBX
LX
LX 
  B  X  aB QB 
L
dt
s
p
B
V




 bVLX W L
XL X 


 aV QV 
L
p
V

 
Проблема идентификации модели
Большое количество неизвестных из статистики параметров
имитационной модели определяем косвенным образом, сравнивая
выходные временные ряды переменных модели с доступными
статистическими временными рядами. В качестве критериев близости
расчетного X и статистического Y временных рядов используем
индекс несовпадения Тэйла T: U = 1 – T, - и коэффициент похожести
D, построенный на основе вейвлет коэффициентов.
T
U ( X ,Y )  1 
 X
t  t0
T
X
t  t0
~ X W
~Y
D( X , Y )  cos   W
j,k
j,k
j,k
2
t
t
 Yt 
2
T
  Yt 2
t  t0
~
W jZ,k 
W jZ,k  2 j
 W
j ,k
Z
j ,k
2j

2
Параллельные вычисления с GRID








Цепочка выполнения приложения в GRID-среде:
(1) выбор задания
(2) ввод необходимых параметров по форме, сгенерированной по
описанию сервиса-оболочки на языке WSDL
(3) запуск приложения на счет в GRID-среде;
(4) отслеживание состояние выполнения задания на
соответствующей странице портала;
(5) получение пользователем оповещения о вы-полнении задания
(или аварийном его завершении) и ссылки на результаты
(6) визуализация результатов расчета временных рядов
макропоказателей в Excel-файле.
Опыт создания распределенной среды на основе кластеров ВЦ
РАН, ИВМ РАН
Проверка работоспособности модели
Выпуски продукции в секторах экономики Кировской области
70 000.0
60 000.0
50 000.0
40 000.0
30 000.0
20 000.0
10 000.0
0.0
2000
2010
2020
Y_X
2030
Y_Y
2040
Y_Z
2050
Базовый сценарий
Запас «белых» WX и «черных» BX денег в секторе X
8 000 000.0
7 000 000.0
6 000 000.0
5 000 000.0
4 000 000.0
3 000 000.0
2 000 000.0
1 000 000.0
0.0
2000
2010
2020
WX
2030
2040
BX
2050
Базовый сценарий
Предложение труда в секторах экономики
500 000.0
450 000.0
400 000.0
350 000.0
300 000.0
250 000.0
200 000.0
150 000.0
100 000.0
50 000.0
0.0
2000
2010
2020
QL_X
2030
QL_Y
2040
QL_Z
2050
Сценарные численные эксперименты с моделью



Если B(t) – значение некоторого макропоказателя в момент
времени t в базовом сценарии,
а S(t) – значение этого же макропоказателя в текущем
сценарии,
то вариация изменения макропоказателя U(t)
U (t )  100%   S (t ) B(t )  1
Сценарий 1: рост трансфертов сектору Y
U (t )  100%   S (t ) B(t )  1
40%
1000%
800%
30%
600%
20%
400%
200%
0%
2000
10%
2010
2020
2030
2040
-200%
TGX
TGY
TGZ
2050
0%
2000
2010
2020
Y_X
2030
Y_Y
2040
Y_Z
2050
Сценарий 1: изменение индексов цен и
ставок заработной платы
70%
1%
60%
0%
2000
50%
2010
2020
2030
2040
2050
-1%
40%
-2%
30%
-3%
20%
-4%
10%
0%
2000
-10%
-5%
2010
2020
2030
2040
2050
-6%
pX_Y
pX_Z
pX_L
sL_X
sL_V
sL_Y
sL_W
sL_Z
sL_U
Сценарий 2: административный зажим
5%
1.0%
0.8%
4%
0.6%
0.4%
3%
0.2%
2%
0.0%
2000
-0.2%
1%
0%
2000
2010
2020
2030
sL_V
sL_Y
sL_W
2040
2050
-0.4%
-0.6%
2010
2020
2030
2040
2050
-0.8%
-1.0%
-1%
pZ_Y
pZ_X
pZ_L
sL_X
sL_Z
sL_U
Сценарий 2: административный зажим
5.0%
1.6%
1.4%
4.0%
1.2%
1.0%
3.0%
0.8%
2.0%
0.6%
0.4%
1.0%
0.2%
0.0%
2000
2010
2020
pU_X
2030
pU_Y
2040
pU_L
2050
0.0%
2000
2010
2020
WL
2030
2040
WG
2050
Сценарий 3: инновационный
400.0%
300.0%
350.0%
300.0%
250.0%
250.0%
200.0%
200.0%
150.0%
150.0%
100.0%
100.0%
50.0%
0.0%
2000
50.0%
2010
2020
Y_X
2030
Y_Y
2040
Y_Z
2050
0.0%
2000
2010
2020
QK_X
2030
QK_Y
QK_Z
2040
2050
Сценарий 3: инновационный
0%
2000
2010
2020
2030
-5%
2040
2050
20.0%
15.0%
-10%
10.0%
-15%
5.0%
-20%
0.0%
2000
-25%
2010
2020
2030
2040
-5.0%
-30%
pX_Y
pX_Z
pX_L
pV_Y
pV_Z
pV_L
2050
Сценарий 3: инновационный
400.0%
20.0%
15.0%
300.0%
10.0%
200.0%
5.0%
100.0%
0.0%
2000
2010
2020
2030
2040
2050
0.0%
2000
-5.0%
pV_Y
pV_Z
pV_L
2010
2020
TXG
2030
TYG
2040
TZG
2050
Литература





Оленев Н.Н., Шатров А.В. Концепция использования
имитационной модели экономики региона для исследования его
инновационного потенциала. // Мат. моделир. развивающейся
экономики: Сб. тр. летн. шк. по эконом.-матем. моделированию
ЭКОМОД-2006. – Киров: ВятГУ, 2006. – 152 с. С. 10-24.
Оленев Н.Н., Поспелов И.Г., Стариков А.С. Опыт идентификации
вычислимой модели экономики. Труды XLVII научной
конференции МФТИ. 2004. Ч.VII. С.171-172.
Оленев Н.Н. Основы параллельного программирования в
системе MPI. М.: ВЦ РАН. 2005. 80 с.
Бурнаев Е.В., Оленев Н.Н. Меры близости на основе вейвлет
коэффициентов для сравнения статистических и расчетных
временных рядов // Межвуз. сб. научн. и научно-метод. тр. за
2005 г. Киров: ВятГУ, 2006. C.41-51.
Горбачев В.А., Оленев Н.Н. Трехсекторная имитационная
модель региональной экономики // Труды 49 научной
конференции МФТИ, 24-25 ноября 2006 г. Ч.VII. C. 96-98.