Решение уравнений с модулями
реклама

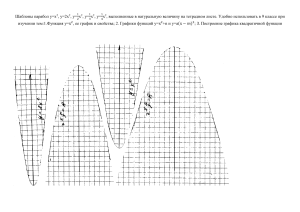
Решение уравнений с модулями Определение Модулем числа называется само число, если оно неотрицательно, противоположное число, если оно отрицательно. Примеры: |3-5|=5-3 |-х2 | = х2 |П-3| = П-3 Уравнение 1 Решаем уравнение, не раскрывая модуль, а используя свойства |a| 0 и |a|=|-a| |2x – 4| = 10 – 5x При условии, что 10-5х 0, х 2, имеем: 2х-4=10-5х 7х=14 Х=2 ОТВЕТ: 2 или 2х-4=-10+5х -3х=-6 х=2 Уравнение 2 Х2+4х+|x+3|+3=0 Решаем по определению модуля. x+3, если х -3 |x+3|= -х-3, если х < -3 1 способ Х+3 0 х -3 х2 + 4х+х+3+3=0 Х2 + 5х + 6=0 Х=-2 (не уд.) Х=-3 2 способ Х+3<0, x<-3 Х2 + 4x-x-3+3=0 Х2 + 3x=0 X (x+3) = 0 X=0 (НЕ УД.) или Х=-3 ОТВЕТ:-3 Уравнение 3 | Х2 + x-3|=x В этом уравнении нерационально использовать определение модуля. И при условии, что X 0, имеем: Х2 + х – 3=х Х2 + х -3=-х Х2 = 3 Х2 +2х-3=0 Х= 3 D=16 х =- 3 (не уд.) Х1=1 Х2=-3 (не уд.) ОТВЕТ: 3, 1 Уравнение 4 |3Х2 - 6x – 1| = 2|3-x| Возможны два случая при решении. При решении этого уравнения используем утверждение: |a|=|b|<===> a=b a=-b 1 способ 3Х2 - 6х-1=6-2х 3Х2 - 4х – 7 = 0 D=100 Х1=7/3 Х2=-1 2 способ 3Х2 - 6х – 1 = -6+2х 3Х2 - 8х + 5 = 0 D=4 Х1=5/3 Х2=1 ОТВЕТ: -1, +1, 5/3, 7/3 Уравнение 5 Х2 - 3Х2/|х|=0 О.Д.З х не равен 0 1 случай Х>0 Х2 – 3х =0 Х|x-3|=0 X=0(не уд.) или х=3 2 случай Х<0 Х2 + 3x = 0 X (x+3) = 0 X=0 (не уд.) или х =-3 ОТВЕТ: -3, +3 №6 Для каждого значения параметра решить уравнение и привести геометрическую интерпретацию полученного решения: |x-2| = a Если а<0, то корней нет Если а=0, то |x-2| =0, т.е. х=2 Если а>0, то x-2=a x= 2+a x-2=-a x= 2-a №7 |x-a| = x Если а=0, то |х|= х верно для всех неотрицательных х Если а<0, то |х-1|= х Х-1=х или х-1=-х х=1/2 =) При а=0, х принадлежит [0; а<0, то нет корней a>, то х = а/2 ]