05_Лекция
реклама

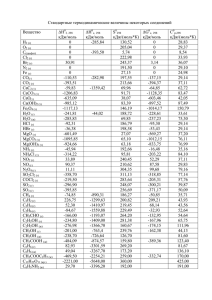
Основные понятия химической термодинамики. Первый закон термодинамики. Термохимия. Второй закон термодинамики. Направление химических процессов Одкрытые Закрытые Изолированные Виды энергии Виды механического движения а б [энергия]=[работа]=Дж или кДж в Энергия Механическая форма Кинетическая энергия Потенциальная энергия Еда и дистанция Внутренняяя энергия U: ΔU=Uкінц-Uпоч. Есть два способы передачи энергии от или до системы: 1. передача теплоти 2. виконання роботи. Теплота обозначается Q. Q=mcΔT, Зміна температури при ендотермічних процесах Зміна температури при екзотермічних процесах Работа А=pΔV, Внутренняя энергия (U) U Eп Ек (1) 0 Еп – суммарная потенциальная энергия взаимодействия молекул Ек – суммарная кинетическая энергия движения молекул Для идеального газа: Ек Е N 3 Е kT 2 N N А Еп = 0 3 U Ек Е N kT N А 2 k NА R 3 3 U RT pV 2 2 Работа в термодинамике A F S cosα 1) Изохорный процесс (V=const) A F 0 cosα A0 Работа в термодинамике A F S cos α 2) Изобарный процесс ( р F const ) S* S h2 h1 F рS * A рS* (h2 h1) рV S F h2 h1 A рV2 pV1 RT2 RT1 A рV RT p Работа в термодинамике численно равна площади фигуры под графиком процесса в координатах р(V)! p 0 1 V 2 р V1 V2 V Работа в термодинамике Какую работу совершил газ при переходе из состояния 1 в состояние 2? р,атм 2 1 6 10 3 м 3 2 Работа газа в термодинамике численно равна площади фигуры под графиком процесса в координатах р(V)! 2 10 5 Па 1 0 2 4 6 8 V,л А 6 10 2 10 1200 Дж 3 5 Работа в термодинамике Какую работу совершил газ при переходах: 1 → 2, 2 → 3, 3 → 4, 4 → 1. Найти работу газа за цикл. р,атм 3 1 0 2 6 10 3 м 3 А12 0 А3 4 0 3 5 А23 6 10 3 10 1800 Дж 3 5 А41 6 10 1 10 600 Дж 3 5 5 2 3 1010 Па Па А 5 1800 600 1200 Дж 110 Па 4 1 2 4 6 10 3 м 3 6 8 V,л 3 А 6 10 2 10 1200 Дж 5 Работа газа за цикл численно равна площади фигуры внутри цикла процесса в координатах р(V)! Работа в термодинамике Идеальный газ расширяется по закону р=V. Найти работу, совершенную газом при увеличении объема от V1 до V2. Работа газа в термодинамике численно равна площади фигуры под графиком процесса в координатах р(V)! p2 p А 2 V2 1 p1 V1 0 V1 (V2 V1 ) V2 V V2 V1 (V2 V1 ) 2 (V2 V1 ) А (V2 V1 ) 2 А 2 (V 2 V1 ) 2 2 Работа в термодинамике В каком из переходов газ совершил наибольшую работу? Ответ обосновать. 2p p p 2 1 3 2p 2T 2 3 4 p 4 T T p 1 V 0 V 2V 4V А34 А23 А41 А12 Газ находится в вертикальном цилиндре с площадью основания 0,01 м2 при температуре 27°С. На расстоянии 0,8 м от дна цилиндра находится поршень массой 20 кг. Атмосферное давление нормальное. Какую работу совершит газ при его нагревании до 37 °С? Дано: м2 S=0,01 t1= 270C t2= 370C h1=0,8м mп=20кг р0=105Па А? 10 А 5 р const pV1 T А RT S F h2 h1 Т1 pV RT mп g p р0 S pV1 R Т1 V1 Sh1 mп g р0 Sh1 р0 S mп g h1 S T А T Т1 Т1 0,01 20 10 0,8 10 32 Дж 300 Ответ: 32 Дж Первый закон термодинамики F F в неш ΔU A F S cosα Q U A A Авнеш Q Q U Aвнеш Первый закон термодинамики запрещает вечный двигатель первого рода Деревянный барабан Одноатомный газ сначала изобарически расширился в четыре раза, а затем в результате изохорического нагревания его давление возросло в три раза. Начальное давление газа 100 кПа, его конечный объём 12 л. Нарисовать графики процессов, протекающих с газом, в координатах (р,V), (р,Т) и (V,Т). Найти работу, совершённую газом, и изменение его внутренней энергии. р,кПа р,кПа 3 300 100 0 1 3 2 12 V,л 3 300 100 1 2 0 T 4T T 12T 12 3 V,л 2 3 1 0 T 4T T 12T 3 3 3 100 10 Па 9 10 м 900 Дж А 100кПа 9 л 3 3 U pV U ( p3V3 p1V1 ) 2 2 3 U (3600 300) 4950 Дж 2 Идеальный газ при изобарном нагревании и изотермическом расширении получил 16 кДж тепла. При этом его внутренняя энергия увеличилась на 6 кДж. Нарисовать графики процессов с газом в координатах (р, V) и (V,Т). Какую работу совершил газ при изотермическом расширении? Дано: Q=16 кДж ΔU= 6 кДж А23 ? 1 2 V р р1 1 2 U 2 3 0 3 р2 V 0 V1 V2 3 U12 U RT 2 2 А12 RT U 3 5 Q12 А12 U12 U 3 V3 V3 3 V2 2 V1 1 0 T1 T T2 23 Q23 А23 Q Q12 5 А23 Q U 3 56 6кДж А23 16 3 Ответ: 6 кДж. Одноатомный газ расширяется сначала изобарно, а затем изотермически. Работа, совершаемая газом при расширении, равна 800 Дж. В процессе изотермического расширения газ получил 300 Дж тепла. Найти изменение внутренней энергии газа. Дано: A=800 кДж Q23 300 Дж ΔU- ? 1 2 23 р р1 1 2 Q23 А23 U 23 3 р2 V 0 V1 V2 V3 U 2 3 0 Q23 А23 U U12 А12 А А23 500 Дж А12 RT U U12 3 3 RT А 750 Дж 2 2 Ответ: 750 Дж. Одноатомный газ, занимающий объём 2 л при давлении 100 кПа, нагревают сначала при постоянном давлении, а затем при постоянном объёме. При этом газ совершает работу 100 Дж, а его температура возрастает вдвое. Какое количество тепла сообщили газу при нагревании? Нарисовать графики процесса нагревания газа в координата (р, V) и (р,Т). Ответ: 400 Дж. Дано: V=2 л A=100 Дж T3=2T1 Q13 ? р р 3 p3 p1 1 p1 2 1 3 p3 2 T V 0 V1 V2 0 T1 T2 T3=2T1 Нагреватель Тн КПД тепловых машин Qн А Qн Qх Qн Qн Рабочее тело (Газ) Qх Холодильник Тх А Qх 1 Qн p 3 U pV 2 Qн 2 3p p 3 4 1 0 V Qх 4V V T 1→2 2→3 3→4 4→1 pV = const р V T p const T = const V = const const T p const T = const V const = const T Q A U Qн Q13 Qн A13 U13 ΔU Q 0 >0 >0 Н >0 >0 >0 Н 0 <0 <0 Х <0 <0 <0 Х A Контакт Работа в термодинамике Какую работу совершил газ при переходах: 1 → 2, 2 → 3, 3 → 4, 4 → 1. Найти работу газа за цикл. р,атм 3 1 0 2 6 10 3 м 3 А12 0 А3 4 0 3 5 А23 6 10 3 10 1800 Дж 3 5 А41 6 10 1 10 600 Дж 3 5 5 2 3 1010 Па Па А 5 1800 600 1200 Дж 110 Па 4 1 2 4 6 10 3 м 3 6 8 V,л 3 А 6 10 2 10 1200 Дж 5 Работа газа за цикл численно равна площади фигуры внутри цикла процесса в координатах р(V)! p 3p 2 3V 3 23рр p 0 1 V 4 V 4V А 2 р 3V 6 pV А13 3 р 3V 9 pV 3 U pV 2 3 U13 ( p3V3 p1V1 ) 2 3 U13 (3 p 4V pV ) 2 33 U 13 pV 16,5 pV 2 Qн A13 U13 Qн 9 рV 16,5 рV 25,5 рV А 6 рV 0,235 Qн 25,5 рV Ответ: =23,5% p 2 1 0 p 3 2 3 1 4 V 4 0 V 4 T 3 1 2 0 T А Qн Qх Qн Qн Нагреватель Тн Qн Рабочее тело (Газ) Qх Холодильник Тх А Для ИТМ А Тн Т х Qн Тн Реактивный двигатель на твердом топливе Прямоточный реактивный двигатель поток воздуха Энтальпийная диаграмма Тепловой эфект расстворения 1 моль H2SO4+1 моль Н2О ΔНрозч,289 =-28,07 кДж; 1 моль H2SO4+100 моль Н2О ΔНрозч,298 =-73,39 кДж; 1 моль H2SO4+1000 моль Н2О ΔНрозч,298 =-86,32 кДж; Н-д СаО(г) + СО2(г) = СаСО3(к) ΔНf298=-177,88 кДж/моль, ΔS298=-160,48 Дж/град·моль, ΔG298=-177,88-(298·(-0,16048))= -130,22 кДж/моль Н-д СаСО3(к)=СаО(к)+СО2(г) ΔНf298=177,88 кДж/моль, ΔS298=160,48 Дж/град·моль, ΔG1500=177,88-(1500·(0,16048))= 62,84 кДж/моль