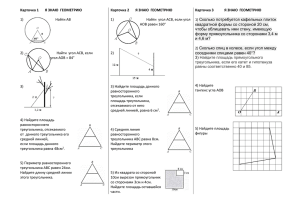
Соотношения между сторонами и углами треугольника
реклама

Уважаемые девятиклассники! Предлагаю вам задания для самостоятельной работы по математике с целью улучшения четвертной отметки. Желающие могут решить один из вариантов ко вторнику (9 декабря) на отдельном листочке. Тема Соотношения между сторонами и углами произвольного треугольника Вариант 1 1. В треугольнике ОРК назовите угол, противолежащий стороне РК данного треугольника. 2. В треугольнике МСЕ назовите угол, образованный сторонами МЕ и СЕ данного треугольника. 3. В ΔМРК МК = р, ∠М = α, ∠Р = β. Найдите РК. 4. В ΔАВМ АВ = m, ВМ = а, ∠В = β. Найдите АМ. 5. В ΔМСР РС = 8 см, РМ = 5 см, sin M = 0,6. Найдите значение синуса угла С 6. В ΔРМС РС = 3 см, СМ = 4 см, РМ = 5 см. Найдите значение косинуса меньшего угла. 7. В ΔМРК МК = 10 см, sin Р = 0,8. Найдите радиус окружности описанной около треугольника. 8. В Δ СРЕ СР = 8 см, РЕ = 15 см, СЕ = 17 см. Найдите площадь треугольника с помощью формулы Герона. 9. Диагонали параллелограмма АВСМ, равные 12 см и 10 см образуют, угол 60⁰. Найдите длину большей стороны параллелограмма. 10. В треугольнике АВС стороны равны 7 см, 8 см, 12 см. Докажите, что треугольник АВС тупоугольный. Вариант 2 1. Из трех выражений: 1) 𝑎2 + 𝑏 2 − 2𝑎𝑏 cos 𝛾; 2) 𝑎2 + 𝑐 2 − 2𝑎𝑐 cos 𝛽; 3) 𝑐 2 + 𝑏 2 − 2𝑐𝑏 cos 𝛼; 2. Найдите сторону треугольника, если две другие стороны равны 7 см и 9 см, а угол между ними равен 60⁰. 3. В треугольнике АВС АВ = 4 см, ВС = 6 см, АС = 9 см. найдите радиус описанной около треугольника окружности. 4. Диагонали параллелограмма равны 8 см и 6 см, а угол между ними равен 60⁰. Найдите меньшую сторону параллелограмма. 5. Площадь треугольника равна 3√3 см2. Две его стороны равны 3 см и 4 см. найдите третью сторону треугольника, если данные стороны образуют: а) тупой угол; б) острый угол.