Урок геометрии в 8 классе
реклама

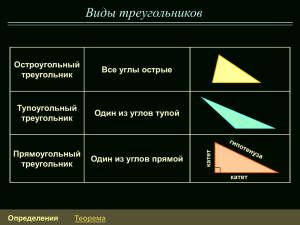
Урок геометрии в 8 классе Бермудские острова, владение Великобритании в северо-западной части Атлантического океана, близ берегов Северной Америки. Занимает около 150 островов, из которых обитаемы только около 20. Площадь 53,3 км². Острова были открыты испанским мореплавателем Х. Бермудесом в 1522 г. Пуэрто-Рико, содружество Пуэрто-Рико, владение США в Вест-Индии, на о. ПуэртоРико и близ лежащих островах Площадь 8,9 км².Административный центр – Сан-Хуэн. Официальный язык испанский. Флорида, полуостров на юговостоке Северной Америки, часть шт. Флорида(США). Площадь 115 тыс. км². Пальмы на полуострове Флорида. Треугольник В ∆АВС – треугольник А,В,С - вершины АВ, ВС, АС – стороны LA,LB,LC -углы А А С Виды треугольников 3 1 2 4 Равнобедренный треугольник Две стороны равны Углы при основании равны Биссектриса, проведённая к основанию, является медианой и высотой Равносторонний треугольник Все стороны равны Углы все равны Прямоугольный треугольник 30° с в 90° а Один угол прямой Сумма двух острых углов равна 90° Катет, лежащий против угла в 30° равен половине гипотенузы (а = ½с) с² = а² + в² S = ½а·в Сумма углов треугольника В треугольнике сумма углов равна 180° . ∟A+∟B+∟C =180° Если сумма углов в треугольнике меньше 180° , то такого треугольника не существует. Признаки равенства По двум сторонам и углу между ними По стороне и двум прилежащим к ней углам По трём сторонам ФАЛЕС древнегреческий учёный и философ, основатель ионийской(милетской) школы. Фалес первым стал доказывать геометрические теоремы; ему принадлежат доказательство следующих положений: 1) круг делится диаметром пополам; 2) в равнобедренном треугольнике углы при основании равны; 3) при пересечении двух прямых образуемые ими вертикальные углы равны. Пирамида Хеопса Фараон IV династии Хеопс воздвиг самую большую из египетских пирамид, которая была самым высоким сооружением в течении последующих 4 тысячелетий(высота пирамиды – 146,6 м, длина каждой из сторон основания – 230 м). На постройку пирамиды Хеопса ушло около 2,3 миллиона каменных блоков весом до 2,5 т. «Определение подобных треугольников» <А =<М, <В=<N, <C=<K В ÀÂ BC AC MN NK MK N А С М K ∆АВС и ∆МNK – подобны АВ и MN,BC и NK, AC и MK – сходственные стороны k – коэффициент подобия Задача №1 Дано: ∆АВС и ∆МNK <А = 63°,<В = 56° АВ = 4,ВС = 3, АС = 6 <M = 63°, <N =56° МN = 8, NК = 6, МК = 12 Определите подобны ли треугольники? Задача № 2 Дано: ∆АВС подобен ∆МNК АВ = 3, ВС = 4, АС = 6, МN = 12. Найти: NK и МК. Задача № 3 Дано: ∆АВС подобен ∆MNK <А = 30°, <В = 85°, <С = 65°. Найти: <M, <N, <K. Подобные фигуры Домашнее задание: §1.п.57, 65, №541. Спасибо за урок