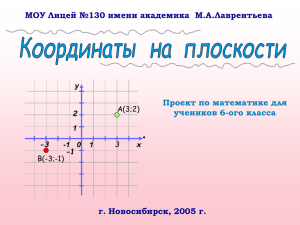
Построение графиков функций
реклама

Построение графиков функций Способы представления функции Способ, при котором каждому значению аргумента x соответствует одно значение функции y(x) называется явным. Задавая значения x, вычисляется значение y. При таком представлении кривая графика функции не может быть замкнутой. Способ, при котором x и y вычисляются как функции некого параметра t называется параметрическим. Задавая значения t, функция x(t) вычисляет значение x, функция y(t) вычисляет значение y. Построить графики функций при явном представлении Анализируя графики функции, ответьте на вопросы: 1. Функция является возрастающей или убывающей. 2. Принимает ли функция нулевое значение. 3. Есть ли интервал, на котором функция меняет знак. Построить графики функций при параметрическом представлении окружность эллипс улитка Паскаля астроида циссоида строфоида эпициклоида произвольная кривая Виды систем координат Прямоугольная система координат, в которой координаты точки на плоскости определяются как взятые со знаком расстояния от точки до осей системы координат (x, y) Полярная система координат задается лучом, который называют полярной осью. Любая точка на плоскости определяется координатами Полярный радиус - расстояние от точки до полюса. Полярный угол может изменяться в диапазоне от 0 до 2. За положительное значение полярного угла принимается угол, определенный против часовой стрелки. Перевод полярных координат в прямоугольные выполняется с помощью тригонометрических уравнений Построить графики функций, заданных в полярных координатах полярная роза спираль Архимеда Лемниската кардиоида (частный случай улитки Паскаля) «Бубновый туз» Будьте любопытными, поинтересуйтесь историей появления полярных координат, узнайте при моделировании каких процессов целесообразно использовать полярные координаты, какие кривые являются частными случаями по отношению друг к другу. Какие еще кривые, кроме предложенных могут быть описаны полярными координатами. Как перевести прямоугольные координаты в полярные.