Треугольники и их виды
реклама

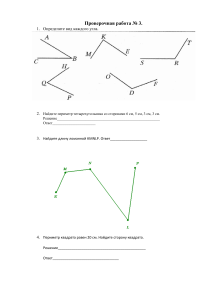
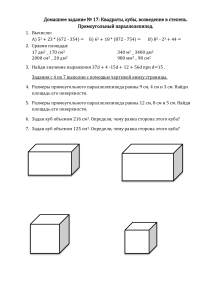
Содержание 1. Треугольники: по виду углов; по виду сторон; 2. Прямоугольники; 3. Другие четырехугольники. Цели: Познакомить учащихся с классификацией треугольников по сторонам и углам; Развивать представление о прямоугольниках; Сформировать понятие равных фигур; Научить находить площадь и периметр; Познакомить с единицами измерения площадей; Познакомить с другими видами многоугольников. Треугольник – это геометрическая фигура состоящая из трех точек, не лежащих на одной прямой и трех отрезков попарно их соединяющих. А В С АВС – это самый простой многоугольник. Треугольник в зависимости от величины угла тупоугольный прямоугольный остроугольный А АВС – остроугольный В С Д ДВМ – прямоугольный В М N NOC - тупоугольный С O Треугольники в зависимости от числа равных сторон равнобедренный разносторонний равносторонний А АВС – равносторонний, АВ=АС=ВС С В М РМО – равнобедренный, Р О Д СДА - разносторонний С А РМ=МО Прямоугольник – это которого все углы прямые. А а четырехугольник, В в Д АВСД – прямоугольник а – длина, в – ширина <А = <В = <С = <Д = 900 С у Прямоугольник, у которого все стороны равны, называется квадратом. А а В а Д АВСД – квадрат АВ=ВС=СД=ДА С Периметр прямоугольника Р = (а+в)*2, где а - длина, в - ширина, а, в – смежные стороны. Периметр квадрата Р = 4*а, где а – сторона квадрата. Диагонали прямоугольника равны А В О Д С АС = ВД - диагонали Равенство фигур Две геометрические фигуры называют равными, если их можно совместить друг с другом, наложив одну на другую. Площадь прямоугольника S = а*в, где а - длина, в - ширина, а, в – смежные стороны. Площадь квадрата S = а2, где а – сторона квадрата. Единицы площади мм2 см2 дм2 м2 км2 ар гектар 1 км2 = 1 000 000 м2 1 дм2 = 100 см2 1 м2 = 100 дм2 1 см2 = 100 мм2 1 ар = 100 м2 1 га = 100 ар = 10 000 м2 a=6 см b=2 см S = 6*2 = 12 (см2) -параллелограмм -трапеция -ромб Решите тест Литература Математика 5-6 класс под ред. Г. В. Дорофеева, И. Ф. Шарыгина - 2010; Геометрия 7-9 класс под редакцией Л. С. Атанасяна, В. Ф. Бутузова и др. – 2009; История математики