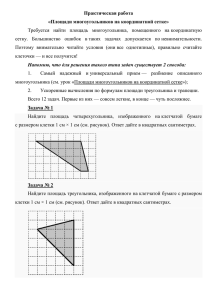
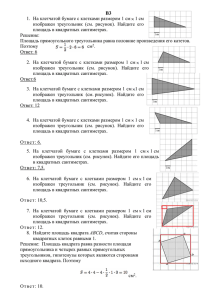
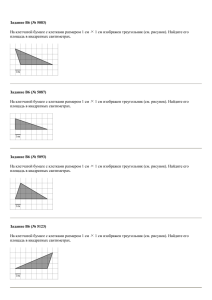
Задания В6.
реклама

Варианты решений задания В6 Петрунина Елена, Кузьменкова Анастасия В6- это задание, которое невозможно решить без знания формул площадей геометрических фигур. Вот некоторые формулы, которые необходимо знать: Произвольный треугольник. a, b, c – стороны; a – основание; h – высота; 1.Задание B6 (№ 27543) На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. Решение: ABC-треугольник h где h – высота, а – основание S= ½(2*6)=6 Ответ: 6 a 2.Задание B6 (№ 27544) На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. Решение: ABC-треугольник 1) где h – высота, а – основание 2)S= ½(2*6)=6 Ответ: 6 h a 3.Задание B6 (№ 27545) На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. Решение: ABC-треугольник a 1) где h – высота, а – основание 2)S=½ (8*3)=12 Ответ: 12 h 4.Задание B6 (№ 27546) На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. Решение: ABC-треугольник 1) где h – высота, а – основание 2)S=½ (2*6)=6 Ответ:6 h a 5.Задание B6 (№ 27547) На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. Решение: B 1)АВС-треугольник ½ (4*5)=10 Sᴀᴅᴄ= ½ (1*5)=2.5 A Sᴀᴃᴅ= Sᴀᴃᴄ- Sᴀᴅᴄ=10-2,5=7,5 2)Sᴀᴃᴄ= Ответ:7,5 D C 6.Задание B6 (№ 27548) На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. Решение: 1)досторим данную фигуру до трапеции APRC. S(ABC)=S(APRC)- S(APB)-S(CBR) 2)S(APRC)=(3+5)*5/2=37,5 S(APB)=3*2/2=3 S(CBR)=5*2/2=5 3)S(ABC)=37,5-3-5=29,5 Ответ:29,5 A P B C R 7.Задание B6 (№ 27549) На клетчатой бумаге с клетками размером 1 см 1 см изображен треугольник (см. рисунок). Найдите его площадь в квадратных сантиметрах. Решение: 1) AC=6 BK=2 B 2)S=(6 Ответ: 12 *2 )/2=12 A C 8.Задание B6 (№ 27550) На клетчатой бумаге с клетками размером 1 см 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. Решение: ABCD-прямоугольник S=ab, Где a-сторона, b-сторона S=4*7=28 Ответ: 28 9.Задание B6 (№ 27551) Найдите площадь квадрата ABCD, считая стороны квадратных клеток равными 1. Решение: ABCD- квадрат 1)S=a2, Где а – сторона S=32=9 Ответ: 9 10.Задание B6 (№ 27552) Найдите площадь прямоугольника ABCD, считая стороны квадратных клеток равными 1. Решение: ABCD-прямоугольник 1) S=ab, Где a-сторона, b-сторона 2)S=2*4=8( Ответ: 8 11 .Задание B6 (№ 27553) На клетчатой бумаге с клетками размером 1 см 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. Решение: B A Рассмотрим два треугольника ∆ ABD и ∆ CBD O D C в треугольнике ∆ ABD AO является высотой и равна 3 см ,BD=4см воспользуемся формулой S ᴀᴃᴅ=½*4*3=6 Второй треугольник идентичен первому значит полученную площадь надо умножить на 2. S ᴀᴃᴄᴅ= 6*2=12 Ответ: 12 12 . Задание B6 (№ 27554) На клетчатой бумаге с клетками размером 1 см 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. Решение: Рассмотрим два треугольника ∆ ABС и ∆ADC В ∆ ABС основание AC=5,высота BF=2 По формуле Вычисляем площадь ∆ ABС S ᴀᴃᴄ =½*5*2=5 В ∆ADC основание AC=5,а высота DG=3 Вычисляем площадь ∆ ADС S ᴀᴅᴄ = =½*5*3=7,5 S ᴀᴃᴄᴅ=5+7,5=12,5 Ответ:12,5 B A G F D C 13 . Задание B6 (№ 27555) На клетчатой бумаге с клетками размером 1 см 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. B Решение: Соединим точки A и C Рассмотрим ∆ ABC и ∆ ADC В ∆ ABC основание AC=6,высота BO=4 Вычисляем площадь ∆ ABС по формуле D A S ᴀᴃᴄ =½*6*4=12 В ∆ ADC основание AC=6,высота DO=2 S ᴀᴅᴄ =½*6*2=6 S ᴀᴃᴄᴅ= S ᴀᴃᴄ - S ᴀᴅᴄ S ᴀᴃᴄᴅ=12-6=6 Ответ:6 O C 14 . Задание B6 (№ 27556) На клетчатой бумаге с клетками размером 1 см 1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах. K B Решение: Данная фигура-трапеция с основаниями BC и AD BC=6 ; AD=1 Проведем высоту DK=5 По формуле Вычисляем площадь трапеции S ᴀᴃᴄᴅ=((6+1))*5/2=17,5 Ответ:17,5 A D C 15.Задание B6 (№ 27557) На клетчатой бумаге с клетками размером 1 см 1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах. Решение: Данная фигура-трапеция с основаниями BC и AD BC=4 ; AD=1 Проведем высоту DF=6 По формуле Вычисляем площадь трапеции S ᴀᴃᴄᴅ=((4+1)*6)/2=15 Ответ:15 B A F D C 16.Задание B6 (№ 27558) На клетчатой бумаге с клетками размером 1 см 1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах. Решение: Данная фигура-трапеция с C основаниями BC и AD BC=5 ; AD=2 Проведем высоту BF=4 По формуле Вычисляем площадь трапеции S ᴀᴃᴄᴅ=((5+2)*4)/2=14 B A F D Ответ:14 B A 17.Задание B6 (№ 27559) На клетчатой бумаге с клетками размером 1 см 1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах. F D C Решение: Данная фигура-трапеция с основаниями BC и AD BC=9 ; AD=4 Проведем высоту BF=5 По формуле Вычисляем площадь трапеции S ᴀᴃᴄᴅ=((9+4)*5)/2=32,5 Ответ:32,5 18.Задание B6 (№ 27560) На клетчатой бумаге с клетками размером 1 см 1 см изображена трапеция (см. рисунок). Найдите ее площадь в квадратных сантиметрах. A D B K C Решение: Данная фигура-трапеция с основаниями BC и AD BC=4 ; AD=1 Проведем высоту BF=4 По формуле Вычисляем площадь трапеции S ᴀᴃᴄᴅ=((1+4)*4)/2=10 Ответ:10 19.Задание B6 (№ 27561) На клетчатой бумаге с клетками размером 1 см 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. Решение: B C Продлим сторону AK и опустим перпендикуляр CD Данная фигура – трапеция с основаниями AD=8 и BC=3,и высотой CD=4 Находим площадь трапеции по формуле S ᴀᴃᴄᴅ=((8+3)*4)/2=22 A K D Найдем ∆ CDK по формуле S ᴄᴅᴋ=½*5*4=10 Затем находим S ᴀᴃᴄᴋ= S ᴀᴃᴄᴅ -S ᴄᴅᴋ S ᴀᴃᴄᴋ=22-10=12 Ответ:12 20.Задание B6 (№ 27562) На клетчатой бумаге с клетками размером 1 см 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах. В ответе запишите S/π . Решение : R=4 ∟ a=90ᵒ=π/2 Воспользуемся формулой S=π*R²- (π/2*R²)/2 S=16 π-(π/2*16)/2=16π-4π=12π Ответ: 12 21.Задание B6 (№ 27563) Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (9;9). Решение: В ∆ ABC основание AC=9-1=8 Высота BС=9-6=4 Воспользуемся формулой S ᴀᴃᴄ =½*8*4=16 Ответ:16 22.Задание B6 (№ 27564) Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (7;9). Решение: В ∆ ABC основание AC=9-1=8 Высота BG=9-6=4 Воспользуемся формулой S ᴀᴃᴄ =½*8*4=16 Ответ:16 23.Задание B6 (№ 27565) Найдите площадь треугольника, вершины которого имеют координаты (1;6), (9;6), (10;9). Решение: Продлим сторону AL и опустим перпендикуляр BC В ∆ ABC основание AC=10-1=9 Высота BС=9-6=4 Воспользуемся формулой S ᴀᴃᴄ =½*9*4=18 Рассмотрим ∆ BCL , основание CL=1, Высота BС=9-6=4 S ᴃᴄᴌ=½*4*1=2 Находим S ᴀᴃᴌ= S ᴀᴃᴄ - S ᴃᴄᴌ S ᴀᴃᴌ=18-2=16 Ответ:16 Б6 (№25678) .Найдите площадь равнобедренного треугольника, если его боковая сторона равна 5, а основание-6. 24.Задание В Решение: S=1/2*6 Ответ:12 А С =12 25.Задание B6 (№ 27567) Найдите площадь трапеции, вершины которой имеют координаты (4;3), (10;3), (10;9), (4;9). B A C D Решение: Данная фигура-трапеция с основаниями BC и AD BC=10-4=6 ; AD=10-4=6 Проведем высоту BF=9-3=6 По формуле Вычисляем площадь трапеции S ᴀᴃᴄᴅ=((6+6)*6)/2=36 Ответ:36 26.Задание B6 (№ 27568) Найдите площадь прямоугольника, вершины которого имеют координаты (1;1), (10;1), (10;7), (1;7). B C D Решение: Данная фигурапрямоугольник AB=7-1=6 ; AD=10-1=9 По формуле S=a*b Вычисляем площадь S=6*9=54 Ответ: 54 27.Задание B6 (№ 27569) Найдите площадь четырехугольника, вершины которого имеют координаты (8;0), (10;8), (2;10), (0;2). B C D Решение: Данная фигураквадрат AB=10-2=8 ; AD=10-2=8 По формуле S=a2 Вычисляем площадь S=82=64 Ответ : 64 28.Задание B6 (№ 27570) Найдите площадь четырехугольника, вершины которого имеют координаты (8;0), (9;2), (1;6), (0;4). B A C D Решение: Данная фигурапрямоугольник AB=6-4=2 ; AD=9-1=8 По формуле S=a*b Вычисляем площадь S=8*2=16 Ответ : 16 29.Задание B6 (№ 27571) Найдите площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (8;6), (5;6). B A F Решение: Данная фигура-трапеция с основаниями BC и AD BC=8-5=3 ; AD=10-1=9 C Проведем высоту BF=6-1=5 По формуле Вычисляем площадь трапеции S ᴀᴃᴄᴅ=((3+9)*5)/2=30 Ответ: 30 D 30.Задание B6 (№ 27572) Найдите площадь параллелограмма, изображенного на рисунке. А D В Решение: 1) ABCD- параллелограмv 2)Воспользуемся формулой S=a*h 3)S=2*3=6 С Ответ:6 31.Задание B6 (№ 27573) Найдите площадь трапеции, вершины которой имеют координаты (1;1), (10;1), (10;6), (5;6). Решение: A D B L C 1)ABCD-трапеция. АВ=10-5=5 DC=10-1=9 AL=6-1=5 2)Воспользуемся формулой S=(5+9)*5/2=35 Ответ: 35 32.Задание B6 (№ 27574) Найдите площадь параллелограмма, изображенного на рисунке. Решение: A D C B 1)ABCDпараллелограмм S=BC * h S=3*2=6 Ответ: 6 33.Задание B6 (№ 27575) Найдите площадь четырехугольника, вершины которого имеют координаты (1;7), (8;2), (8;4), (1;9). Решение: 1)ABCDпараллелограмм S=a*h 2)S=7*2=14 A D B Ответ: 14 C 34.Задание B6 (№ 27576) Найдите площадь трапеции, изображенной на рисунке Решение: A D B C 1)ABCD-трапеция АВ=6-2=4 DC=3-1-2 AH=4-1=3 2)Воспользуемся формулой S=(4+2)*3/2=9 Ответ:9 35.Задание B6 (№ 27577) Найдите площадь четырехугольника, вершины которого имеют координаты (1;7), (4;5), (4;7), (1;9). Решение: A B D C 1)ABCD-параллелограмм AB=4-1=3 AD=9-7=2 S=a*h S=3*2=6 Ответ: 6 d^2=2*2 d=2 36.Задание B6 (№ 27583) Найдите диагональ квадрата, если его площадь равна 2. Решение: 1)т.к. ABCD- квадрат,то d^2=2*2 d=2 Ответ : 2 37.Задание B6 (№ 27584) Найдите сторону квадрата, площадь которого равна площади пря\-моугольника со сторонами 4 и 9. Решение: 1)S( квадрата)=a2 S(прямоугольника)=l*b a2=l*b=4*9=36 a=6 Ответ:6 38.Задание B6 (№ 27585) Найдите площадь параллелограмма, если две его стороны равны 8 и 10, а угол между ними равен 30 . Решение: 8 S=a*b*sin альфа= 8*10*1/2=40 Ответ:40 30 10 S=8*10*sin30=8*10*1/2= =40 Ответ:40 39.Задание B6 (№ 27586) Найдите площадь ромба, если его стороны равны 1, а один из углов равен 150 . Решение: 1)Воспользуемся формулой S=1^2*sin30=0,5 Ответ: 0,5 40.Задание B6 (№ 27587) Найдите площадь прямоугольного треугольника, если его катеты равны 5 и 8. Решение: 1)т.к. ABC-прямоугольный,то S= a*b/2 S=5*8/2=20 Ответ:20