Вписанная и описанная окружности
реклама
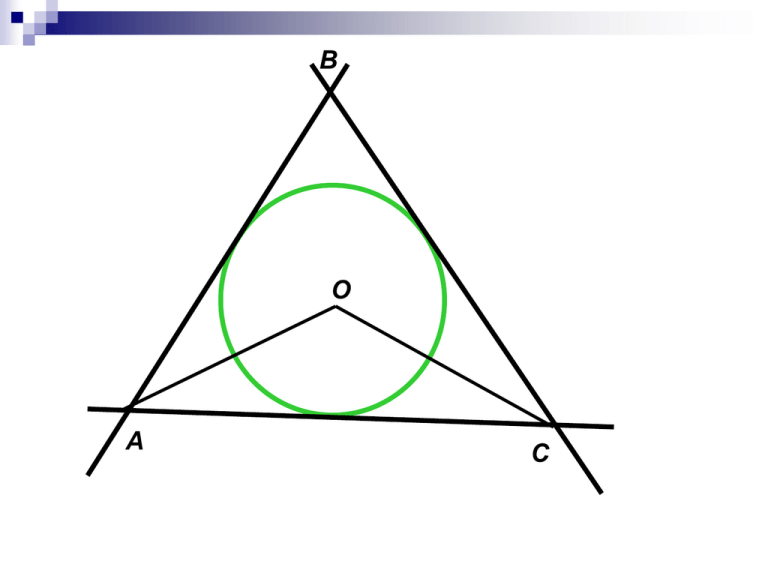
В О А С А О В 5 7 М 3 К С Р А 2 5 Вписанная и описанная окружности окружность, вписанная в многоугольник окружность, описанная около многоугольника где лежат центры вписанных и описанных около треугольника окружностей свойство и признак описанного и вписанного четырехугольника Описанная окружность Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника. Многоугольник в этом случае вписан в окружность. Вписанная окружность Если все стороны многоугольника касаются окружности, то окружность называют вписанной в многоугольник. Многоугольник в этом случае описан около окружности. Теорема: В любой треугольник можно вписать окружность 1. 2. 3. 4. 5. Проведем биссектрисы треугольника. Точка пересечения – точка О. Проведем перпендикуляры к каждой стороне из точки О. OK=OL=OM (по св. бисс. угла) Точки K, L, M – точки касания окружности с центром в т. О и радиусом ОК. Окружность является вписанной в треугольник Теорема: Около любого треугольника можно описать окружность. 1. 2. 3. 4. 5. Проведем серединные перпендикуляры к сторонам треугольника. Точка пересечения – точка О. Проведем отрезки ОА, ОВ, ОС. ОА = ОВ = ОС (по св-ву серед. перпендикуляра к отрезку). Точки А, В, С лежат на окружности с центром в точке О и радиусом ОА. Окружность является описанной около треугольника. Где лежат центры вписанных и описанных около треугольника окружностей? О – точка пересечения биссектрис О – точка пересечения серединных перпендикуляров Свойство и признак описанного и вписанного четырехугольника Свойство: В любом описанном четырехугольнике суммы противоположных сторон равны В А С AB + CD = AD + BC D Признак: Если суммы противоположных сторон четырехугольника равны, то в него можно вписать окружность Свойство: В любом вписанном четырехугольнике сумма противоположных углов равна 180 градусам В А С D Признак: Если сумма противоположных углов четырехугольника равна 180 градусам, то около него можно описать окружность.





