Виды трапеции Остроугольная трапеция • Остроугольной трапецией называется

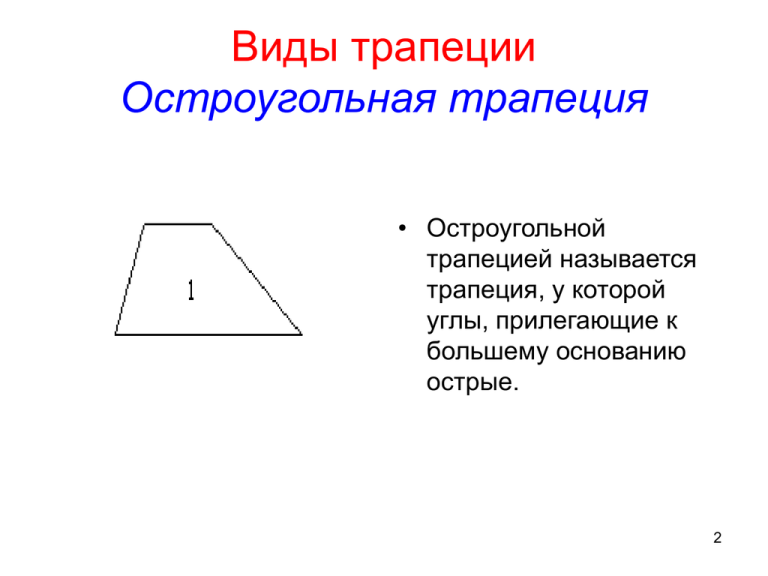
Виды трапеции
Остроугольная трапеция
• Остроугольной
трапецией называется
трапеция, у которой
углы, прилегающие к
большему основанию
острые.
2
Тупоугольная трапеция
• Тупоугольной трапецией
называется трапеция, у
которой один из углов,
прилегающих к
большему основанию
тупой.
3
Равнобедренная трапеция
• Равнобедренной
(равнобокой,
равнобочной)
называется трапеция, у
которой боковые
стороны равны.
4
Прямоугольная трапеция
• Прямоугольной
называется трапеция, у
которой одна боковая
сторона
перпендикулярна
основаниям
5
Определите вид трапеции
6
Свойства трапеции
•
Средняя линия трапеции
параллельна основаниям и
равна их полусумме.
Дана трапеция АВСD. КМсредняя линия. Через точки В и
М проведем прямую.
Продолжим сторону AD за точку
D до пересечения с ВМ.
Треугольники ВСМ и МРD равны
по стороне и двум углам,
поэтому ВМ=МР или точка М середина ВР. КМ является
средней линией в треугольнике
АВР. По свойству средней линии
треугольника КМ параллельна
АР и в частности АD и равна
половине АР.
7
Свойства трапеции
•
Диагонали делят
трапецию на четыре
части, две из которых,
прилежащие к боковым
сторонам,равновелики.
•
Треугольники АВD и АСD
равновелики: у них равные
высоты и общее основание.
Эти треугольники имеют
общую часть АОD.
Следовательно площади
красных треугольников
равны.
8
Свойства трапеции
• если трапеция
равнобокая, то около
нее можно описать
окружность;
• если сумма оснований
равна сумме боковых
сторон, то в нее можно
вписать окружность
9
Свойства равнобокой трапеции
•
Углы, прилежащие к каждому из
оснований равнобокой
трапеции, равны.
•
Докажем равенство углов А и D при
большем основании AD трапеции
АВСD. Для этой цели проведем
через точку С прямую
параллельную боковой стороне АВ.
Она пересечет большое основание
в точке М. Четырехугольник АВСМ
являеся параллелограммом, т.к. по
построению имеет две пары
параллельных сторон.
Следовательно, отрезок СМ,
заключенный внутри трапеции
равен её боковой стороне: СМ=АВ.
Отсюда ясно, что СМ=СD,
треугольник СМD - равнобедренный,
СМD=СDM, и, значит, А=D. Углы,
прилежащие к меньшему
основанию, также равны, т.к.
являются для найденных
внутренними односторонними.
10
Свойства равнобокой трапеции
• Диагонали равнобокой
трапеции равны.
Рассмотрим треугольники
АВD и ACD. Они равны по
двум сторонам и углу между
ними (АВ=СD, AD - общая,
углы А и D равны по
свойству равнобокой
трапеции). Поэтому АС=BD.
11
Площадь трапеции
В
А
С
D
H
• Площадь трапеции
равна произведению
полусуммы её
оснований на высоту
• Формула
S=1/2(AD+BC)*BH
12
Доказательство
B
C
A
H
F
D
Доказательство:
Рассмотрим трапецию ABCD c
основаниями AD и BC ,
высотой BH и площадью S.
Докажите, что
S=1/2(AD+BC)*BH.
Диагональ BD разделяет трапецию
на два треугольника ABD и
BCD, поэтому
S=S(ABD)+S(BCD).
Примем отрезки AD и BH за
основание и высоту
треугольника ABD, а отрезки
BC и DF за основание и высоту
треугольника BCD. Тогда
S(ABD)=1/2AD*BH,
S(BCD)=1/2*CB*DF. Т.к. DF=BH,
тогда S(BCD)=1/2*CB*BH.
S=1/2AD*BH+1/2
BC*BH=1/2(AD+BС)*ВН.
13
Трапеции в жизни
15