Документ 4760966

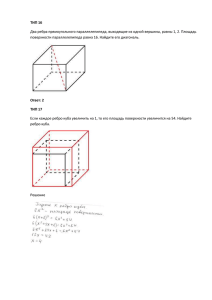
1)Определения.
2)Общие замечания о положении центра шара.
3)Комбинация шара с призмой.
4)Комбинация шара с пирамидой.
5)Комбинация шара с усеченной пирамидой.
6)Комбинация шара с телами вращения.
7)Задачи
8)Применение
9)Формулы
10)Задания
11)Список литературы
12)Список сайтов
S
Выпуклый многогранник
называется вписанным, если
все его вершины лежат на
некоторой сфере. Эта сфера
называется описанной для
данного многогранника.
.
B О
A
C
D
S
.
B
A
.
О
.R
C
.
D
Выпуклый многогранник
называется описанным, если
все его грани касаются
некоторой сферы. Эта сфера
называется вписанной для
данного многогранника.
1. Центр шара, вписанного в
многогранник, лежит в точке
пересечения
биссекторных
2. Центр шара,
описанного
плоскостей
всех двугранных
около
многогранника,
лежит в
углов
многогранника.
точке
пересечения Он
расположен
только внутри
плоскостей,
многогранника.
перпендикулярных
ко всем
ребрам многогранника и
проходящих через их
середины. Он может быть
расположен внутри, на
поверхности и вне
многогранника.
.
О
•Сферу
можно
описать
•Центр
сферы,
описанной
около около
•Сферу,
в частности,
можнооколо
описать:
призмы
в том илежит
только
том
прямой
нав середине
прямойпризмы,
треугольной
призмы,
около
правильной
призмы,
около
случае,
если
призма
прямая ичерез
высоты
призмы,
проведенной
прямоугольного
параллелепипеда,
около
около
ее основания
можно
описать
центр
круга,
описанного
около
прямой четырехугольной призмы, у
окружность.
основания.
которой сумма противоположных углов
основания равна 180 градусов.
B
.
.О
L.
K
A
E
D
C
F
•Сферу
можно вписать
прямуюв прямые:
•Сферу,
в частности,
можно ввписать
•Центр
сферы,
прямую
призму
в правильную,
томвписанной
и только четырехугольную
в втом
случае,
треугольную,
призму,
лежит
впротивоположных
середине
высоты
если всуммы
основание
призмы
можно сторон
(у которой
призмы,
проходящей
через
центр
вписать
окружность,
а высота
основания
равны
между собой)
припризмы
условии Н
окружности,
вписанной
в основание.
равна
этой окружности.
= 2r,
где Н диаметру
– высота
призмы,
r – радиус круга,
вписанного в основание.
О
.
.
.
.
O
DM=OK
D
M
K
.A
O.
.B
АО=ОВ
•Центр сферы, вписанной в пирамиду, у
•Если
боковые
грани пирамиды
которой боковые грани
одинаково
наклонены
наклонены к
к основанию, лежит в одинаково
точке пересечения
•В правильную
пирамиду
можно вписать
сферу.
высоты пирамиды
с биссектрисой
линейного
основанию,
то в такую
пирамиду
угла любого двугранного
углавписать
при
можно
сферу.
основании пирамиды, стороной которого
служит высота боковой грани, проведенная
S
из вершины пирамиды.
S
B
A
O
B
S
.R
D
A
B
C
A
D
O
C
.
.
D
C
•Около пирамиды можно описать
сферу в том и только в том случае,
если около ее основания можно
описать окружность.
•Центр сферы, описанной около
пирамиды лежит в точке пересечения
прямой, перпендикулярной основанию
пирамиды, проходящей через центр
окружности, описанной около этого
основания, и плоскости,
перпендикулярной любому боковому
ребру, проведенной через середину
этого ребра.
S
A
C
O
B
S
A
C
O
K
B
•Если боковые ребра пирамиды равны между
собой (или равно наклонены к плоскости
основания), то около такой пирамиды можно
описать сферу. Центр этой сферы в этом случае
лежит в точке пересечения высоты пирамиды
(или ее продолжения) с осью симметрии
бокового ребра, лежащей в плоскости бокового
ребра и высоты.
•Сферу, в частности, можно описать: около
треугольной пирамиды, около правильной
пирамиды, около четырехугольной
пирамиды, у которой сумма
противоположных углов равна 180
градусов.
S
.O
B
A
L
C
D
•Около любой
правильной
усеченной
пирамиды
можно описать
шар. (Это
условие
является
достаточным,
но не является
необходимым)
•В правильную
усеченную
пирамиду
можно вписать
шар в том и
только в том
случае, если
апофема
пирамиды
равна сумме
апофем
оснований.
•Около цилиндра, усеченного
конуса (прямых круговых), конуса
можно описать сферу.
O
О
•В усеченный
•В любойконус
конус(прямой
(прямойкруговой)
можно
вписать можно
сферу ввписать
том и только
круговой)
сферу. в
том случае, если его образующая равна
сумме радиусов оснований.
O
.
•В цилиндр (прямой круговой)
можно вписать сферу в том и
только в том случае, если A
цилиндр равносторонний.
S
.O
S
.
.
A
B
О
O
B
Решение:
Задача №1. Найдите площадь
шара, вписанного в
конус. Если угол между образующей и плоскостью
основания равен 60, высота равна 3 3 .

S
Дано:
SAB-конус
M
(О;OK)
Ðàññì î ò ðèì SAK=60
ÀÎ Ì  ÀÎ Ê
3 AB; SA  наклонная;
SК=
SK  ( ABK ) 
SK3 
(ò .ê.   ï ðÿì î óãî ëüí û å, ï î ýò î ì ó
Рассмотрим

АKS
:
SK
перпендику
ляр;
Найти:
ðàâí
û
ï
î
äâóì
ñò
î
ðî
í
àì
),
1) Рассмотрим SAK : SO  3; A
АК - проекция
SAK
SAK S=?

60

ASK
между
3060

угол
Ì ÀÊ
OK

OM

r
çí à÷èò : Î ÀÌ  Î ÀÊ 

 30,
2
2
прямой SA и плоскостью АВК
ÀÌ  MS  ÀÊ
.
.
L
O
К
S
L
B
M
O
B
K
A
S
L
M
O
B
A
K
Ðàññì î òðèì ABS: AM  MS  AK2  KB  SL  LB 


3
2
 ABS 5ðàâí
î
ñòî
í
í
èé



) S  4r  4 
 12(ед)


 SK  BM  AL  ì åäèàí û , áèññåêòðèñû
è âû ñî òû 
2
ðî
SO 2
SO

 (ñ÷èòàÿ î ò âåðø èí û )  OK  r 

OK 1
2
2
Ответ: 12 ед
2
3
 
2
3

Решение:
Задача №2. Найти
цилиндр (высота-h, радиус-r)
максимальной боковой поверхности, вписанный
в данный конус (высота-H, радиус-R).
S x 
max
+
-
R
r
S x 
Дано:
0
2
Конус
R е Hточки
RH:  2 r
Найдем Н-высота
критически
S2
R  и H
R
2
HBAC :см
 B
S

rh
б.п.
Рассмотрим

SAM

AM
SM
б.п.

Возьмем производну
ю : 2S  2
Rr4 r 2  
R-радиус
H
(
R

)

(Пусть
приравняем
производну
юцилиндра
к нулю
)
h
-2высота

;

,
HR
H
R
2

r(R
r)H


1)hSAM
ьно
BAC
- общий
BC
h
Следовател
SR
Цилиндр
BO
r
2H
H
2
R
2R R 2
( RR r-радиус
2)AMS
22
rrR

) ACB,
0, R  2r  0; r 
R
H(R
- r)
R
2 R
значит
h

Найти:
поэтомуRH
SAMBAC
С
2
Ответ : S-?смR
A
4
S
H
S
M
h
B
O
r
O
h
A
R-r C
M
Задача №3. В шар с радиусом 5 вписан цилиндр
Решение:
с высотой Н. Найдите
радиус основания цилиндра.
Дано:
(O;OR)
H-высота
Цилиндр
А
2) По теореме Пифагора
.O R
R
2 Найти:
2цилиндра8
1) AC 2 образующая
 ВС 
Ar
4r  4 R R=?h  r  АС4см
r
В
 АВС  прямоуголь ный
2
.
H
C
Ответ: 4cм
H
C
.
O
R
B
В строительную фирму поступил заказ на проектирование
Решение:
и постройку дома цилиндрической
формы с радиусом
основания 10 м. Крыша сферической формы, но комната
должна иметь форму прямоугольного параллелепипеда
с высотой потолка 2,5 м и наибольшей площади.
Дано:
r  10м
h  2,5 м
Найти:
S ж.п.  ?
Т .к. ABCDEFKL  прямоуголь ный параллелепипед,
значит : АЕ  ЕО, поэтому АОЕ - прямоуголь ный,
F
E
H
G
следовательно : АО 2  ЕО 2  АЕ 2
ЕО  ЕО 2  АЕ 2 ; ЕО  100 
25
5 15
; ЕО 
4
2
A
B
О
D
C
Диогонали
прямоуголь
ника
делятся
точкой
пересечени
я пополам
,
Пусть
АВ  х(-мпрямоуголь
), тогда
: ник,
23))Так
как
АВСD
поэтомуАВ
 АD,
поэтому
2  2х
S теореме
у, поэтому
S AC
375
поэтому
: BD
2 EOПифагора
 5 ный;
15
:х BD
 x.  y 2 ; y  BD 2  x 2
По
АВD
-хпрямоуголь

BD
2
A

Возьмем производную : S ( х)  х  375 - х  х 375  х
2
 375  х 
2
2х2
375  х 2
2


х
B
О
C
D
у
Найдем критические точки
( Приравняем производную к нулю) :
2х2
375  х 
2
375  х
375  х 2  2 х 2
375  х 2
х1  5 15
2
0
max
S x 
0
х2  5 15  посторонний корень
S x 
+
0
5 15
хmax  5 15 ( м)
ymax  750  375  375  5 15 (м)
S max  5 15  5 15  375 м2
Ответ: 375м 2
х
Проектирование необычных фасадов зданий.
Поиск наиболее удобных сочетаний внешнего
вида дома и внутренней жилой площади.
Нахождение наибольших объёмов при заданных
параметрах строительства.
O
S
.О
O
A
B
Можно ли описать сферу (шар) около:
а) куба
да
б) прямоугольного
параллелепипеда
в) наклонного
параллелепипеда
нет
нет
Справедливо ли утверждение,
что около любой треугольной
пирамиды можно описать сферу?
да
нет
Можно ли описать сферу около
любой четырехугольной пирамиды?
да
При каком условии центр сферы, описанной
около прямой треугольной призмы, лежит:
внутри призмы?
вне призмы?
В основании призмы:
остроугольный
треугольник
тупоугольный
треугольник
нет
При каком условии центр сферы,
описанной около
прямой треугольной призмы,
будет находится на одной
из боковых граней призмы?
Около треугольной призмы
описана сфера, центр
которой лежит вне призмы.
Какой треугольник является
основанием призмы?
В основании лежит
прямоугольный
треугольник
Тупоугольный
треугольник
В основании прямой призмы лежит ромб.
Можно ли в эту призму вписать сферу?
да
нет
Во всякий ли конус можно вписать сферу?
да
нет
Можно ли описать сферу около наклонной призмы?
да
нет
Можно ли описать сферу около
цилиндра (прямого кругового)?
да
Можно ли описать сферу
около конуса, усеченного
конуса (прямых круговых)?
Во всякий ли цилиндр можно
вписать сферу?
нет
нет
да
да
нет
•А. В. Погорелов. Геометрия: Учебник для 10 – 11 классов
общеобразовательных учреждений
•А.Д. Александров, А.Л. Вернер, В.И. Рыжик. Учебник для
10 класса школ с углубленным изучением математики
•Е. В. Потоскуев, Л. И. Звавич. Геометрия 10 класс:
учебник для общеобразовательных учреждений с
углубленным и профильным изучением математики
•И. М. Смирнова, В. А. Смирнов. Геометрия. 10 – 11 класс:
Учебник для общеобразовательных учреждений
•И. Ф. Шарыгин. Геометрия 10-11 классы: Учебник для
общеобразовательных учебных заведений
•Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев, Л. С.
Киселева, Э. Г. Позняк. Геометрия: Учебник для 10 – 11
классов общеобразовательных учреждений.
www.festival.1september.ru
www.avisnest.narod.ru
www.21205s11.edusite.ru