Что может измерить ДНК-чип?

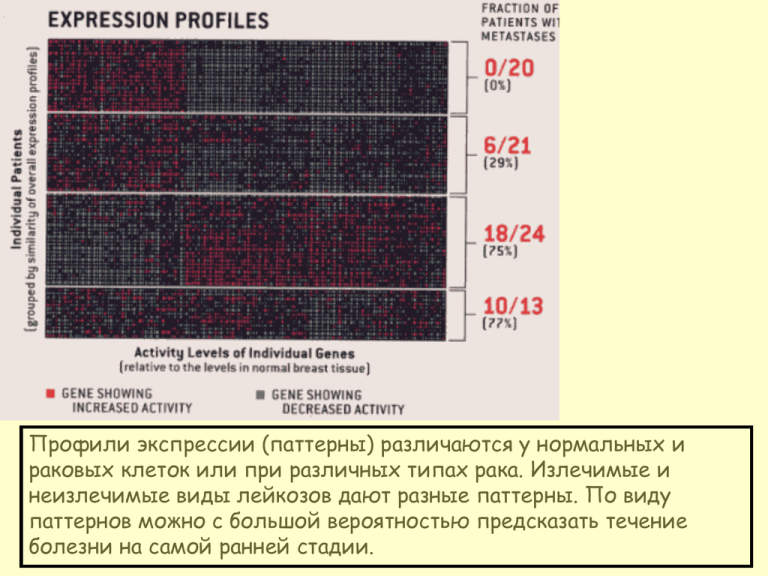
Профили экспрессии (паттерны) различаются у нормальных и
раковых клеток или при различных типах рака. Излечимые и
неизлечимые виды лейкозов дают разные паттерны. По виду
паттернов можно с большой вероятностью предсказать течение
болезни на самой ранней стадии.
Конструкция чипа Affymetrix
PM = perfect match
MM = mismatch
Этапы обработки для чипов Affymetrix
(фирма Affymetrix)
1. Привязка к сетке (gridding)
2. Вычисление значений интенсивности зондов
3. Поправка на глобальный фон
4. Поправка на неспецифическую гибридизацию
5. Вычисление устойчивого среднего логарифмов
поправленных значений в зондах.
6. Масштабирование сигналов чтобы подрезанное среднее
имело фиксированное значение
Проблемы первоначального подхода:
1. MM>PM (60-85% генов, где это
выполняется хотя бы для одного зонда)
Решения
А) Заплатка Affymetrix: идеальный mismatch
Б) А MM вообще не нужен. Вероятностная поправка на фон в
методе RMA.
В) Нет, все-таки будем использовать MM, но с учетом
теоретически вычисленного сродства данной
олигонуклеотидной последовательности. GC-RMA
Проблемы первоначального подхода:
2. Эффект зонда – вариация интенсивности
одного гена, померянная разными зондами
не случайна.
Модель Ли-Вонга. Eg – истинная экспрессия гена g, fi –
чувствительность i-ой пары PM-MM.
PMgi –MMgi =fi Eg + Шум
Произвольное требование, необходимое для идентификации
(f12 +…+fk2)/k =1
Визуальная проверка на присутствие
нелинейной зависимости от
интенсивности. М-А график.
Mg=log(Ig(1)/Ig(2))
Ag=(1/2)log(Ig(1)*Ig(2))
M
0
A
Проблемы первоначального подхода:
3. Нелинейная зависимость от
интенсивности.
Mg=log(Ig(1)/Ig(2))
Ag=(1/2)log(Ig(1)*Ig(2))
Линейная регрессия 1
100
80
y = a+bx
60
40
20
0
0
10
20
30
40
50
60
70
80
90 100
-20
MINa,b((y1-(a+bx1))2+(y2-(a+bx2))2+…+(yk-(a+bxk))2)
Линейная регрессия 2
60
40
20
0
-60
-40
-20
0
-20
-40
-60
20
40
60
Часто бывает полезно
выбрать в качестве
начальной точки отсчета
средние значения
измеряемых величин.
Малиновой и желтой
точкой показаны
величины стандартного
отклонения х и у.
Линейная регрессия 3
2
1.5
1
0.5
Y
0
-2
-1
-0.5
0
1
-1
-1.5
-2
X
R=0.0995, y= 0.995x
2
• Здесь в качестве единиц
измерения выбраны
среднеквадратичные
отклонения для х и у.
• Тогда уравнение прямой,
лучше всего приближающей
наше облако точек имеет очень
простой вид:
• y= R*x
• R – коэффициент корреляции х
и у. При нашем выборе единиц
измерения и начал отсчета
• R=(x1y1+x2y2+…+xnyn)/n
Локально-линейная регрессия (loess)
4
3
2
1
0
3
-1
-2
-3
4
5
6
7
МА график после нормализации
Mn =M – Mloess(A)
Квантильная нормализация
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
1
0.9
0.8
0.7
0.6
0.5
0.4
0.3
0.2
0.1
0
2
3
4
5
6
7
2
3
4
5
6
7
Квантильная нормализация
1
0.9
0.8
0.7
0.6
Series2
0.5
Series1
0.4
Series3
0.3
0.2
0.1
0
1
2
3
4
5
6
7
МА графики для различных иголок принтера
кДНК
микрочип
Поиск генов с одинаковым уровнем
экспрессии в разных образцах
1. Housekeeping гены
К сожалению, не все housekeeping гены имеют
посстоянный уровень экспрессии. Примеры: b -актин,
GAPDH,
2. Гены инвариантного ранга
3. Контрольные гены
Контроли гибридизации bioB, bioC, bioD и cre Гены E.
coli и б/ф P1, биотинилированные сRNA транскрипты
которых вводят в смесь для гибридизации в разных
концентрациях (1,5, 5, 25, 100 pM для bioB, bioC, bioD
и cre, соотв.). BioB – на пороге чувствительности
(1:100000).
Возможная последовательность этапов
обработки для чипов Affymetrix
1 Вычисление “сырых” значений интенсивности зондов
(Affymetrix MicroArray Suit)
2. Поправка на глобальный фон (Affymetrix MAS5)
3. Loess нормализация на уровне зондов (и PM и MM зонды)
4. Вычисление модельного индекса экспрессии (Ли и Вонг,
dChip)
6. Квантильная нормализация индексов экспрессии
Чего с чем нормализуем?
1. И квантильная и лоесс нормализация применяется к паре
чипов. Для нормализации совокупности чипов чаще всего
выбирают (строят) базовый чип и нормализуют все к нему.
а) Базовый чип – это реально существующий чип,
нравящийся автору.
б) Базовый чип конструируется. Как правило, это чип, где
значение каждого гена равно медиане множества значений
этого гена по всем чипам, которые хочется нормализовать.
2. Для квантильной нормализации можно сводить
распределение каждого чипа к множеству средних
квантилей или к множеству квантилей распределения,
построенного по всем чипам сразу.
3. Для лоесс нормализации существует алгоритм “циклический
лоесс”.
Что может измерить ДНК чип
Choe et al. Genome Biology 2005, 6:R16
1
1
2551
14000
генов
на чипе
1.2
87
2
1
141
1.5
1
85
2.5
1.2
1
1
1
90
1
1.5
186
1
14000
генов
на чипе
2.0
88
1
2
3
180
4
1.7
90
1
1
1
180
183
Что может измерить ДНК-чип?
А) Choe et al. Genome Biology 2005, 6:R16
Насколько хорошо ДНК чип выясняет, какие
вообще гены экспрессированы?
•
очень плохо на уровне пары зондов – из зондов,
прошедших через порог, 10% принадлежат
отсутствующим генам, а остальные включают
только 60% присутствующих генов
• Лучше на уровне генов – из генов, прошедших
через порог, 10% принадлежат отсутствующим
генам, а остальные включают 85%
присутствующих генов.
Что может измерить ДНК-чип?
А) Choe et al. Genome Biology 2005, 6:R16
Насколько хорошо ДНК чип выясняет,
какие гены дифференциально
экспрессированы?
•
Плохо, если считать, что дифференциально
экспрессированные означает увеличившиеся
более чем на 20% (из 1309 генов 380 не
находятся (29%), а ошибочно находятся 105(10%
от всех найденных). На самом деле ни один из
генов, увеличивших экспрессию на 20% не был
найден, и лишь половина изменившихся на 50%
была найдена.
• Хорошо, если рассматривать лишь гены,
изменившие экспрессию более чем на 100% (не
находится лишь 7% от так изменившихся при 10%
Возможно ли сравнение результатов
различных экспериментов?
В работе
Multiple Lab Comparison of Microarray Platforms,
Rafael A. Irizarry et al., 2004
рассматриваются результаты измерения одних и тех
же образцов разными лабораториями на разных
платформах. Эффект лаборатории очень велик и
превосходит эффект платформы.
Заметим, что эффект нормализации, особенно
такой, где все образцы нормализуются к одному
экспериментальному образцу, уменьшая
вариабельность результатов отдельного
эксперимента, затрудняет сравнивание различных
экспериментов.
Литература
• Exploration and analysis of DNA microarray and protein
array data. D. Amaratunga, J. Cabrera, Wiley 2004.
• Statistical analysis of gene expression microarray data.
Edited by T. Speed. Chapman and Hall, 2003.
• Statistics for microarrays. E. Wit, J. McClure, Wiley, 2004
• Analyzing microarray gene expressing data.
G. McLachlan, Kim-Anh Do, C. Ambroise, Wiley, 2004
• Bioinformatics and computational biology solutions using
R and Bioconductor. R. Gentleman, V. Carey, W. Huber, R.
Irizzary, S. Dudoit, Springer, 2005.