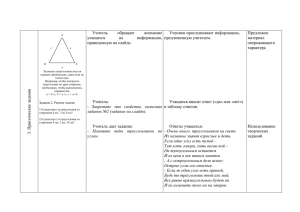
Повторение. Треугольники
реклама

Тема: Треугольник. Конструкции из треугольников Цели урока: - владение учащимися знаниями и умениями предметного содержания темы; - способствовать умению учащихся применять математические знания к решению практических задач; - развитие познавательной активности, творческих способностей учащихся; - воспитание интереса к предмету. Тип занятия: урок формирования и применения знаний и умений. Методы обучения: наглядный, частично – поисковый, практический. Формы организации: коллективная, групповая, индивидуальная. Глядя на мир, нельзя не удивляться! К. Прутков Ход урока 1. Организация начала занятий Вступительное слово учителя Кто не слышал о Бермудском треугольнике, в котором бесследно исчезают корабли и самолёты? А ведь знакомый нам с детства треугольник таит в себе немало интересного и загадочного. Сегодня на уроке мы будем повторять весь изученный материал и каждый раз удивляться полученным открытиям. Условия состязания на уроке 1. Быть внимательным и сообразительным. 2. Не оставлять ни одного вопроса без ответа. 3. На каждое задание затрачивать минимум времени, но максимум усердия. 4. Не подглядывать, не подслушивать, не «проникать в мысли соседа». 2. Актуализация знаний. Мобилизация на успешность 3 – я группа. Назовите вершины и стороны изображенного треугольника? 2 – я группа. Какие виды треугольников вы знаете? 1 – я группа. Дайте определение равнобедренному и равностороннему треугольнику. Класс. Является ли равнобедренным равносторонний треугольник? Почему? Какое неравенство треугольника вам известно? Назовите виды треугольников. Примените неравенство треугольника на практике: определите, какие из следующих треугольников существуют. 3 – я группа. 5 см, 5 см, 5 см; 3 м, 6 м, 3 м. 2 – я группа. 12дм, 3 дм, 8 дм; 12 м , 13 м, 12 м. 1 – я группа. 1 дм, 14 см, 22 см; 3 см, 4 см, 5 дм. 3. Формирование знаний учащихся при решении задач Класс. Что такое периметр треугольника? Что нужно сделать, чтобы найти периметр треугольника? На досках работают два - три человека, выполняя задания своей группы. 1 – я группа. Периметр равнобедренного треугольника равен 21 дм. Известно, что его боковая сторона больше основания в 3 раза. Найдите стороны треугольника. 2 – я группа. В равнобедренном треугольнике основание равно 6 см, а боковая сторона больше основания на 2,5 см. Найдите периметр треугольника. 3 – я группа. Найдите периметр треугольника, если известно, что его стороны равны 8 см, 9 см, 10 см. Проверка 3 – я группа - комментирует решение задачи с места. 2 – я группа - проверка своего варианта на доске, а затем взаимопроверка. 1 – я группа – индивидуально работающий ученик рассказывает решение задачи всему классу. 4. Развитие логического мышления учащихся 3 – я группа. Найдите лишнее слово: сторона, вершина, основание, диаметр, периметр. 2 – я группа. Сколько всего треугольников изображено на рисунке? 1 – я группа. В равнобедренном треугольнике одна сторона равна 25 см, а другая 10 см. Какая из них является основанием треугольника? 5. Развитие познавательного интереса учащихся к изучению предмета 3 – я группа. Сообщение Землемеры Древнего Египта для построения прямого угла пользовались следующим приемом. Бечевку делили узлами на 12 равных частей и концы связывали. Затем бечевку растягивали на земле так, чтобы получился треугольник, со сторонами 3, 4, 5 делений. Угол треугольника, противолежащий стороне с пятью делениями был прямой. В связи с указанным способом построения прямого угла треугольник со сторонами 3,4,5 иногда называют египетским. 1 – я группа. Сообщение Египетские пирамиды – это один из самых грандиозных сооружений, созданных когда – либо руками человека. Самая известная из египетских пирамид – пирамида Хеопса в Гизе. Из – за своих огромных размеров ее иногда называют Большой пирамидой. Ее высота составляет 146,6 м, что примерно соответствует пятиэтажному небоскребу. Строительство пирамиды продолжалось 30 лет. Она состояла из 12 слоев камня и представляла собой ступенчатую гору. Затем ступени были заложены камнями, и ее поверхность стала без выступов. В завершении работ четыре треугольные грани пирамиды были облицованы плитами из ослепительно белого известняка и отполированы до зеркального блеска. Края плит были пригнаны настолько точно, что между ними нельзя было вставить даже лезвие острого ножа. По свидетельству очевидцев, на солнце и при лунном свете гробница Хеопса загадочно сверкала, как огромный светящийся изнутри кристалл. Египетская пирамида Хеопса в Гизе – древнейшее и единственное сохранившееся до наших дней чудо света. Пирамиды бывают 3-, 4- , 5-, 6-ти,…угольные. От чего это зависит? Демонстрация пирамид. 6. Развитие навыков конструирования Треугольники, соединяясь друг с другом, могут образовывать другие фигуры. Например, шесть правильных одинаковых треугольников образуют шестиугольник. 1 – я группа. Равносторонний треугольник разрежьте на три равных треугольника. 2 – я группа. Равносторонний треугольник разрежьте на четыре равных треугольника. 3 – я группа. Разрежьте треугольник на две части и сложите из этих частей прямоугольник. 7. Самостоятельная работа 8. Подведение итогов урока Мы рассмотрели материал по теме «Треугольники. Конструкции треугольников». Закончим урок словами великого ученого Галилео Галилея: «Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать» 9. Задание на дом 10. Рефлексия