й уровень 1- y . Выберите правильное утверждение.
реклама
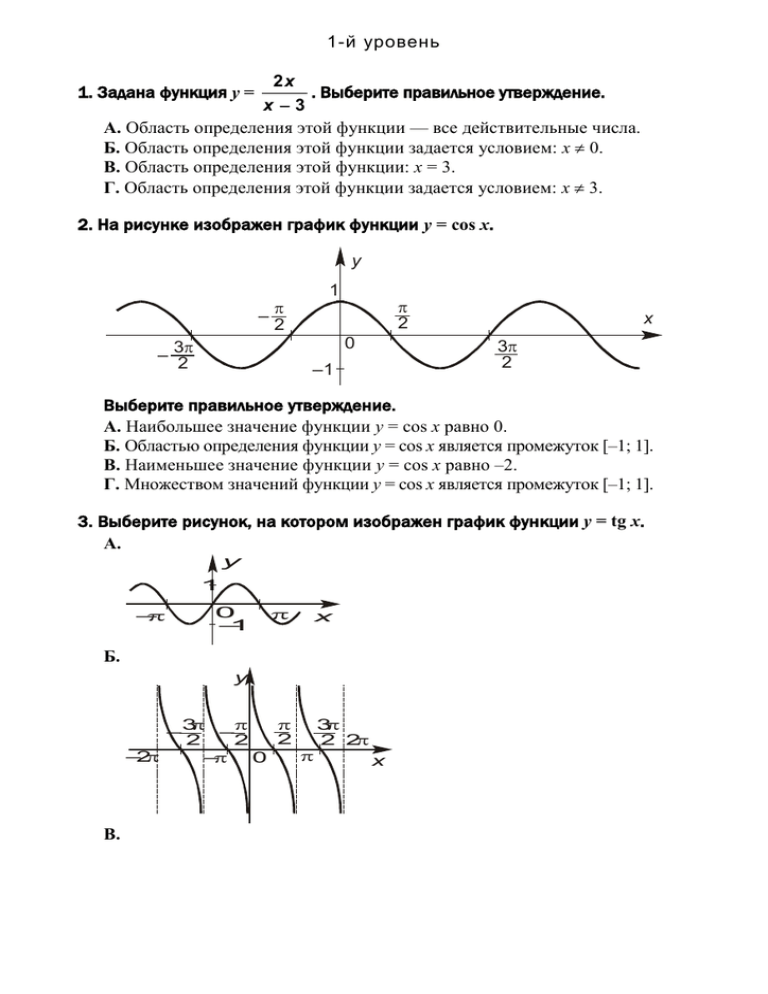
1-й уровень 2x . Выберите правильное утверждение. x3 А. Область определения этой функции — все действительные числа. Б. Область определения этой функции задается условием: х 0. В. Область определения этой функции: х = 3. Г. Область определения этой функции задается условием: х 3. 1. Задана функция y = 2. На рисунке изображен график функции y = соs x. y – 2 1 2 0 – 3 2 –1 x 3 2 Выберите правильное утверждение. А. Наибольшее значение функции y = соs x равно 0. Б. Областью определения функции y = соs x является промежуток [–1; 1]. В. Наименьшее значение функции y = соs x равно –2. Г. Множеством значений функции y = соs x является промежуток [–1; 1]. 3. Выберите рисунок, на котором изображен график функции y = tg x. А. y 1 – 0 – 1 x Б. y 3 –3 – 2 2 2 2 2 –2 – 0 x В. y 2 – – 3 2 – 2 0 3 2 x Г. y 1 3 – 2 2 2 0 –3 –1 2 x 2-й уровень 3 . Отметьте, какие из следующих четырех x 4 утверждений правильные, а какие — неправильные. А. Заданная функция нечетная. Б. Заданная функция четная. В. Область определения этой функции — все действительные числа. Г. Область определения этой функции: х 2. 4. Задана функция y = 2 5. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. А. 30 = . 6 3 Б. sin = –1. 2 В. Если АОС = 30, то синус 30 — это ордината точки А единичной окружности (точка С лежит на положительной полуоси x, точка O — начало координат). 1 Г. sin =– . 6 2 6. На рисунках 1 и 2 изображены графики функций, которые связаны с функцией y = ctg x. y y –2+3 x –+3 0 3 +3 ––3 Рис. 1 –3 0 x –3 2–3 Рис. 2 Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. А. На рисунке 2 изображен график функции y = ctg (x + 3). Б. График функции y = ctg (x + 3) можно получить из графика функции y = ctg x параллельным переносом вдоль оси х на –3 (то есть влево). В. График функции y = ctg (x – 3) можно получить из графика функции y = ctg x параллельным переносом вдоль оси y на +3 (то есть вверх). Г. На рисунке 1 изображен график функции y = ctg (x – 3). 3-й уровень 7. Задана функция y = tg 2x. Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. (2k 1) А. Область определения этой функции: х , где kZ. 4 Б. График этой функции можно получить из графика функции y = tg x, растянув его в два раза вдоль оси y. В. График заданной функции пересекает ось х в точках, для которых k х= , где kZ. 4 Г. График этой функции можно получить из графика функции y = tg x, сжав его в два раза вдоль оси х. 8. Отметьте, какие из следующих четырех утвержд ений относительно свойств тригонометрических функций, связанных с функцией y = cos x, правильные, а какие — неправильные. А. Существует бесконечное множество значений переменной х, для которых cos х = 3 . 2 2 . 3 В. На промежутке (0; ) функция y = cos х убывает. Г. Функция y = 5cos x не имеет наибольшего значения. Б. Функция y = cos 3x + 2 имеет период 9. На рисунках 1 и 2 изображены графики функций, которые связаны с функцией y = sin x. y y 1 – 3 0 – 1 3 2 1 x 0 2 x –3 Рис. 1 Рис. 2 Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. А. На рисунке 1 изображен график функции y = sin x . 3 Б. На рисунке 2 изображен график функции y = 2sin x – 1. В. На рисунке 2 изображен график функции y = sin x – 2. Г. На рисунке 1 изображен график функции y = – sin x . 3 4-й уровень 1 . Отметьте, какие из следующих четырех ctg x утверждений правильные, а какие — неправильные. А. Заданная функция нечетная. k Б. Область определения этой функции: x , kZ 2 В. Множеством значений этой функции является промежуток [0; ]. Г. Заданная функция четная. 10. Задана функция y = 11. Отметьте, какие из следующих четырех утверждений относительно периодичности тригонометрических функций правильные, а какие — неправильные. x А. Функция y = соs х + tg периодическая с периодом 4. 4 Б. Периодическая функция f(x) может иметь область определения х 0. В. Если функция f1(x) периодическая с периодом Т, а функция f2(x) периодическая с периодом 2Т, причем функции f1(x) и f2(x) имеют общую область определения, то функция f (x) = f1(x) + f2(x) всегда будет периодической с периодом 2Т. Г. Функция y = sin 12. Заданы x периодическая. функции y = cos x, y = cos x , y = cos x , соответствие y = cos x и их графики, изображенные в некотором порядке на рисунках 1–3. y 1. – 2 1 2 0 – 1 x y 2. – 2 1 2 0 3. x y 1 0 x – 2 2 Отметьте, какие из следующих четырех утверждений правильные, а какие — неправильные. А. Функция y = cos x может принимать только неотрицательные значения. Б. График функции y = cos x изображен непосредственно под графиком функции y = cos х. В. График функции y = cos x не совпадает с графиком функции y = соs x. Г. График соответствия y = cos x симметричный относительно оси х.