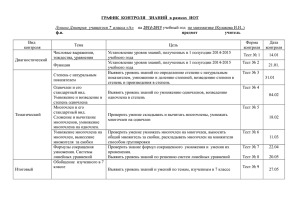
x 2 +y 2

Урок 1. 01.02.2016 алгебра
Самостоятельная работа (письменно в тетради)
I вариант
II вариант
1. Упростите выражение:
1. Упростите выражение:
1) 5(x+8)+2(x-10);
1) 7(x-2)+3(x+8);
2) 15x2(2x+6)-x(9x2-1);
2) y(9y2-1)+15y2(2y+6);
3) a(a2+a-1)-a2(a-1).
3) x2(x-1)-x(x2+x+1).
2. Замените * одночленом так, чтобы
полученное равенство было тождеством:
2. Замените * одночленом так, чтобы
полученное равенство было тождеством:
4)*(x-y)=ax-ay;
4) *(a-b)=ax-bx;
5)(2y-1)*=10y4-5y3;
5) (3x-1)*=6x4-2x3;
6) *(a+b-1)=2ax+2bx-2x.
6) *(m+n-1)=2m2+2mn-2m.
Верно ли утверждение, определение, свойство?
1. Одночленом называют сумму числовых и буквенных множителей.
2. Числовой множитель одночлена, записанного в стандартном виде, называют
коэффициентом одночлена.
3. В результате умножения одночлена на одночлен получается одночлен.
4. Степенью одночлена называют наибольший показатель степени переменных
5. Сумма нескольких одночленов называется многочленом.
6. В результате умножения одночлена на многочлен получается многочлен.
7. Степенью многочлена стандартного вида называют сумму степеней всех
входящих в него одночленов.
8. Чтобы умножить одночлен на многочлен, нужно умножить этот одночлен на
каждый член многочлена и полученные произведения сложить.
9. Одночлены, входящие в состав многочлена и имеющие одинаковые числовые
множители называют подобными членами многочлена.
Устная работа.
1) Замените букву «М» многочленом так, чтобы полученное равенство было
верным:
5а + М = 5а + 3b – 8;
( b2 – bc) - М = b2 – bc – 7b + 5;
М + ( 2a2 + 4аb – b2) = 3a2 + 4ab.
2) В пустое окошко вставьте одночлен так, чтобы полученное равенство было верным:
٠ (a – b) = 4ac – 4bc;
٠ (2a – b) = 10a2 – 5ab.
3) Найдите сумму, разность и произведение одночленов.
Найдите значение выражения 3(3х-1)+5(3-х), если х = -1,5
Решите уравнения
5х +3(х-1) = 4х+11
24х-6х(13х-9) = -13-13х(6х-1)
Домашнее задание: №26.21(в,г), 26.6(в,г), 26.11
Урок 3, урок 4 Умножение многочлена на многочлен
03.02.2016, 04.02.2016 алгебра
1. Устная работа:
1)
8х2 х;
Приведите одночлен к стандартному виду:
9уу2у;
1,2авс* 5а;
2а10в2 (-1,5а3)
2) Приведите подобные слагаемые.
а) 15а + 3в – 4а – в;
б) 7,5х + у – 8,5х – 31,5у;
в) 10 х – 8ху – 3ху;
г) 2ав – 7ав +7а2.
2. Перед нами уравнение: (х – 3)(х + 5) = x2 - 5
Как бы вы начали его решать? (раскрываем скобки). Какое действие надо сделать,
чтобы раскрыть скобки? (Умножить многочлены). Значит, какова тема нашего
урока? (Умножение многочленов. Записываем тему на доске и в тетрадях).Чему мы
должны научиться сегодня? (Мы должны научиться умножать многочлены).
Попробуем дать полный алгоритм умножения многочленов:
1 шаг: каждый член первого многочлена умножаем на каждый
многочлена;
2 шаг: найти произведения полученных одночленов;
3 шаг: привести подобные слагаемые;
4 шаг: полученный многочлен записать в стандартном виде.
4. Вернемся к нашему нерешенному уравнению: (х – 3)(х + 5) = x2 - 5
Теперь мы сможем его решить? (х – 3)(х + 5) = x2 - 5
х2 + 5х – 3х – 15 = x2 - 5
х2 + 2х – 15 = x2 - 5
х2 + 2х – 15 - x2 + 5 = 0
2х – 10 = 0
член второго
2х = 10
х=5
Ответ: 5.
Правило Чтобы умножить многочлен на многочлен, нужно умножить каждый член одного
многочлена поочередно на каждый член другого многочлена а полученные произведения
сложить.
В тетради:
Вариант №1
1. Выполните умножение:
а) (а - 5)(11-b)
б) (-7 - b)(a - 7)
в) (8+3x)(2y -1)
2. Упростите выражение:
а)(3a+5)(3a - 6)+30
б)3b2+(8 - 3b)(b+5)
в)xy(x+y) – (x2+y2)(x – 2y)
Выполнить в тетради
Вариант №2
1. Выполните умножение:
а) (х - 8)(6 - y)
б) (-2 - y)(x-9)
в) (5a - 7)(3a+1)
2. Упростите выражение:
а) (2b - 3)(5b+7)+21
б) 5x2+(3 - 5x)(x+11)
в) xy(x+y) – (x2+y2)(2x - y)
1. Найдите значение выражения:- 2,5x(-2x + 3), если x = 2.
2. Известно, что (3x + a)(x – 4) = 3x2 – 2x – 4a. Найдите значение a и вычислите
значение выражения 3x2 – 2x – 4a при a = -2.
3. Упростите выражение -3x(2x + y) – 4y(3x – 2y) и вычислите значение выражения при
x = -0,1 y = 0,2.
4. Упростите выражение (2x – 5y)(4x + 3y) – (x + 2y)(5x – 6y)
5. Решите уравнение x(x + 1) – (x – 2)(x – 3) = 4.
№27.8(а,б), 27.9(а,б), 27.12(а,б), 27.11(а,в)
Домашнее задание: п.27, №9(в,г), 13(в,г)
Урок 2, урок 5 Геометрия
02.02.2016, 05.02.2016
П.32. Теорема о соотношениях между сторонами и углами треугольника: уметь
доказывать теорему и следствия. П.32 Неравенство треугольника: записать
доказательство теоремы в тетрадь (выучить), решить в тетради №241, 244, 248
Домашнее задание: п32, 33, №246, 250,251, 252