Материалы для подготовки к дифференцированному зачету по
реклама

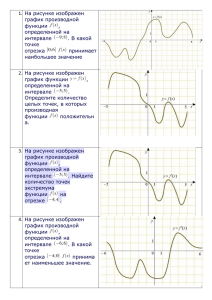
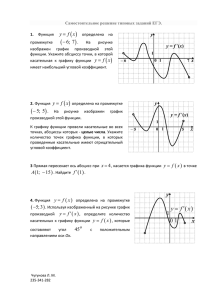
ГБПОУ СО «Артинский агропромышленный техникум» Материалы для подготовки к дифференцированному зачету по теме «Производная» (второй курс) Преподаватель Половникова Н.Н 2016 год На дифференцированный зачет выносятся основные теоретические вопросы, задачи , практическая работа. Каждый билет состоит из 5 заданий: 1. Теоретический вопрос 2. Базовая задача. 3.Практическая работа. 4. Задача практического содержания 5.Презентация «Применение производной». Критерии оценивания. Каждое задание оценивается в 5 – бальной системе, затем выводится итоговая оценка. На зачете можно пользоваться справочным материалом. Образец билета 1. Производные основных элементарных функций 2. На рисунке изображен график функции , определенной на интервале . Найдите количество точек экстремума функции . 3. Практическая работа. Построить фигуру, ограниченную линиями у=х2 + 2, х = 1 х =-2, у = 0 , найти площадь фигуры. 4.Из всех прямоугольников с периметром 12 см найдите и нарисуйте прямоугольник наибольшей площади. 5. Презентация «Применение производной» Справочный материал Произво́дная (функции в точке) — основное понятие , характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению её аргумента при стремлении приращения аргумента к нулю. Процесс вычисления производной называется дифференци́рованием Если — постоянное число и — некоторые дифференцируемые функции, то справедливы следующие правила дифференцирования: …(g ≠ 0) Основные формулы дифференцирования: 1. f ( x) c (c const ) . f ( x) 0. 2. f ( x) x p ( p R) . 3. f ( x) x . 1 . x 5. f ( x) e x . 4. f ( x) 6. f ( x) ln x . 7. f ( x) sin x . 8. f ( x) cos x . 9. f ( x) tgx. 10. f ( x) ctgx. f ( x) p x p 1 . f ( x) 1 . 2 x 1 f ( x) 2 . x x f ( x) e . 1 f ( x) . x f ( x) cos x. f ( x) sin x. 1 . cos 2 x 1 f ( x) 2 . sin x f ( x) Уравнение касательной Y = f(x0) +f′(x0)∙(x – x0) Возрастание и убывание функции. Экстремумы 1) Найти производную функции . 2) Решить уравнение . 3) Отметить корни на числовой прямой, определить знак производной на каждом интервале. Обозначить возрастание, убывание.Найти экстремумы. Записать ответ. Определить наибольшее и наименьшее значение функции Алгоритм решения задачи 1) Найти производную функции 2) Решить уравнение . . 3) Выбрать корни, которые принадлежат промежутку 3) Вычислить значения функции в этих точках и на границах интервала. 4) Выбрать из полученных значений наибольшее (наименьшее) и записать ответ. Исследование функции и построение графиков Исследование функции целесообразно проводить по следующей схеме: 1. Найти область определения D(f) функции. 2. Установить четность или нечетность функции, ее периодичность. 3. Найти точки пересечения графика функции с осями координат. 4. f'(x) = 0; 5. В тех интервалах, где f'(x) > 0, функция возрастает, а где f'(x) < 0, – убывает. Найти точки экстремума. 6.Найти дополнительные точки 7. Построить график функции. Интеграл. Нахождение производных и нахождение неопределенных интегралов (дифференцирование и интегрирование) – это два взаимно обратных действия Решить интеграл – это значит найти определенную функцию некоторыми правилами, приемами и таблицей. F(x)- называется первообразной. Любой неопределенный интеграл имеет вид: – значок интеграла. , пользуясь – подынтегральная функция – значок дифференциала. При записи интеграла и в ходе решения важно не терять данный значок. Заметный недочет будет. – подынтегральное выражение – первообразная функция. – множество первообразных функций, в любом неопределенном интеграле к ответу приплюсовывается константа . Таблица основных неопределенных интегралов. Основные методы интегрирования u, v, w - это функции от x; c - постоянная. Решить определенный интеграл – это значит, найти число с помощью формулы Ньютона-Лейбница: Этапы решения определенного интеграла: 1) Находим первообразную функцию (неопределенный интеграл), константа в определенном интеграле не добавляется. Обозначение является чисто техническим, и вертикальная палочка не несет никакого математического смысла. 2) Подставляем значение верхнего предела в первообразную функцию: . 3) Подставляем значение нижнего предела в первообразную функцию: . 4) Рассчитываем разность , то есть, находим число. Определенному интегралу (если он существует) геометрически соответствует площадь некоторой фигуры Криволинейной трапецией называется плоская фигура, ограниченная осью ,прямыми , и графиком непрерывной на отрезке функции которая не меняет знак на этом промежутке. Пусть данная фигура расположена не ниже оси абсцисс: Тогда площадь криволинейной трапеции численно равна определенному интегралу .. , Задания для зачета. Первые вопросы билетов. 1. Производные основных элементарных функций 2. Производная суммы, разности, произведения, частного. 3. Физический смысл производной. 4. Геометрический смысл производной. 5. Уравнение касательной 6. Возрастание и убывание функций. 7. Экстремумы функций. 8. Наибольшее и наименьшее значение функций. 9. Применение производной к построению графиков функций. 10.Первообразная. 11. Формула Ньютона-Лейбница. 12.Определенный интеграл. 13.Применение интеграла в физике. 14. Применение интеграла в геометрии. 15.Нахождение площади криволинейной трапеции Задания для зачета. Вторые вопросы билетов. 1 Прямая параллельна касательной к графику функции Найдите абсциссу точки касания. 2 Прямая функции . является касательной к графику . Найдите абсциссу точки касания. 3 На рисунке изображен график функции , определенной на интервале . Определите количество целых точек, в которых производная функции положительна. 4 На рисунке изображен график функции , определенной на интервале . Определите количество целых точек, в которых производная функции отрицательна. 5 На рисунке изображен график функции , определенной на интервале . Найдите количество точек, в которых касательная к графику функции параллельна прямой или совпадает с ней. 6 На рисунке изображен график функции , определенной на интервале . Найдите сумму точек экстремума функции . 7 На рисунке изображен график — производной функции , определенной на интервале . Найдите количество точек экстремума функции , принадлежащих отрезку . 8 На рисунке изображен график определенной на интервале касательная к графику функции совпадает с ней. — производной функции , . Найдите количество точек, в которых параллельна прямой или 9 На рисунке изображены график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке . 10 На рисунке изображены график функции и касательная к нему в точке с абсциссой . Найдите значение производной функции в точке . Задания для зачета. Третьи вопросы билетов. 1. Практическая работа. Провести исследование функции у=х3-3х и построить график Исследование функции целесообразно проводить по следующей схеме: 1. Найти область определения D(f) функции. 2. Установить четность или нечетность функции, ее периодичность. 3. Найти точки пересечения графика функции с осями координат. 4. f'(x) = 0; 5. В тех интервалах, где f'(x) > 0, функция возрастает, а где f'(x) < 0, – убывает. Найти точки экстремума. 6.Найти дополнительные точки 7. Построить график функции. 2. Практическая работа. Построить фигуру, ограниченную линиями у=х2 + 2, х = 1 х =-2, у = 0 , найти площадь фигуры. Криволинейной трапецией называется плоская фигура, ограниченная осью ,прямыми , и графиком непрерывной на отрезке функции которая не меняет знак на этом промежутке. Пусть данная фигура расположена не ниже оси абсцисс: Тогда площадь криволинейной трапеции численно равна определенному интегралу .. , Задания для зачета. Четвертые вопросы билетов. 1 Найдите наименьшее значение функции на отрезке 2 Найдите наименьшее значение функции отрезке . на 3 Найдите наибольшее значение функции 4 Найдите наименьшее значение функции . на отрезке на отрезке 5 Найдите наибольшее значение функции на отрезке 6 Найдите точку максимума функции 7 Найдите точку минимума функции . 8 Найдите точку максимума функции 9 Найдите точку минимума функции 10 Найдите наибольшее значение функции . на отрезке . Задания для зачета. Пятые вопросы билетов. Презентация «Применение производной» Примерный план ответа: Определение производной, основные формулы; Значение слова; Применение производной в данной отрасли. Примеры решения практических задач в данной отрасли Выводы Информационные источники Основные источники. 1. Алимов Ш.А. и др. Алгебра и начала анализа. 10 (11) кл. – М., 2000. 2. Атанасян Л.С. и др. Геометрия. 10 (11) кл. – М., 2000. 3. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 10 кл. – М., 2005. 4. Башмаков М.И. Алгебра и начала математического анализа (базовый уровень). 11 кл. – М., 2005. 5. Башмаков М.И. Математика (базовый уровень). 10—11 кл. – М., 2005. 6. Луканкин Г.Л., Луканкин А.Г. Математика. Ч. 1: учебное пособие для учреждений начального профессионального образования. – М., 2004. 7. Математика для техникумов. Алгебра и начала анализа, под ред. Г.М.Яковлева. – М.,1987. 8. Пехлецкий И.Д. Математика: учебник. – М., 2003. Дополнительные источники. 1. Колягин Ю.М., Ткачева М.В, Федерова Н.Е. и др. под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни). 10 кл. – М., 2005. Интернет ресурсы. 1. http://festival.1september.ru 2. http://www.fepo.ru 3. www.mathematics.ru