Лабораторная работа №3:
реклама

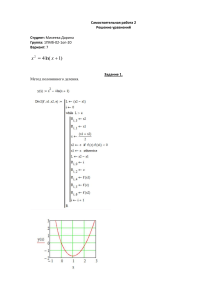
ФГБОУ ВПО «Брянский государственный технический университет» Предмет: «Моделирование систем, модели и методы анализа проектных решений» Лабораторная работа №3: «Численные уравнений» методы решения систем нелинейных Выполнили: Студенты группы 08-САПР Попов И. С. Семченко Е. В. Преподаватель: Филиппова Л. Б. Брянск 2011 Цель работы: изучение численных методов решения нелинейных уравнений и приобретение навыков решения практических задач с использованием программного средства MathCAD. Задание. Погонные потери мощности в прямоугольном металлическом волноводе, выполненном из меди, для основного типа волны H10 определяются по формуле: 2 2b 0.14 1 a 2a 2 b 1 / 2a где потери α определяются в дБ/м (децибел на метр); a и b − поперечные размеры волновода; λ − длина волны. Величины a, b и λ в формулу следует подставлять в сантиметрах. Задавшись указанными в таблице размерами a и b, определите длину волны λ, удовлетворяющую заданному значению α и условию a < λ < 2a. Параметр a, cм b, см α, дБ/м 17-1 2,3 1 0,4 Вариант 17-3 17-4 1,3 1,1 0,65 0,55 0,5 0,4 17-2 1,6 0,8 0,3 17-5 0,9 0,45 0,7 17-6 0,72 0,34 1,2 Теоретическая часть Метод половинного деления Графически процедура поиска корня уравнения f(x) методом половинного деления показана на рис 1. f(x) исходный интервал (b-a) 1 шаг: интервал (b-a)/2 2 шаг: (b-a)/4 3 шаг: (b-a)/8 а xc2 xc3 xc1 b x Рис.1. Графическое представление метода половинного делания Вначале на концах исходного отрезка [a, b], содержащего корень, вычисляют значения функции f(a) и f(b). Затем находят точку, делящую [a, b] на две равные части, по итерационной формуле xc=(a+b)/2 (6) и вычисляют значение функции f(xc). Далее по перемене знака функции выбирают ту половину [a, b], в которой расположен корень. Если знаки f(xc) и f(a) совпадают, то в дальнейшем полагают a = xc и f(a) = f(xc). Если же, напротив, знаки f(xc) и f(a) различаются, а знаки f(xc) и f(b) совпадают, то полагают b = xc и f(b) = f(xc). В результате этих действий получают новый отрезок, содержащий корень. Этот отрезок имеет длину в два раза меньше, чем исходный. Блок-схема алгоритма метода половинного деления(рис.2). Начало Ввод [a,b] Вычисление fa=f(a) fb=f(b) Вычисление xc=(a+b)/2 fc=f(xc) Одинаковы ли знаки fc и fa? нет да a=xc fa=fc нет b=xc fb=fc fc<|(b-a)/xc| да Вывод xc и f c Конец Рис.2. Алгоритм метода половинного деления Готовая программа представлена на рис.3. Рис.3. Программа Код программы описан в приложении 1. Решение задачи с помощью программы и специализированного пакета (MathCAD и т. п.), сравнение результатов. aa 2.3 bb 1 al 0.4 0.14 1 f ( x) 2 bb 2 aa 2 aa al 2 x bb x 1 2 aa x a aa b 2 aa e 0.000000001 pol( f a b e) while ba e c ab 2 b c if f ( a) f ( c) 0 a c otherwise c pol( f a b e) 4.408 f ( pol( f a b e) ) al 0.4 Вывод: В ходе выполнения лабораторной работы получили результаты по исходным данным методом половинного деления. Были использованы программы такие как: MathCAD и Turbo Delphi . Приложение 1. Код программы procedure TForm1.Button1Click(Sender: TObject); var a,b,x,e,tmp:real; i:integer; begin a:=2.3; b:=4.6; e:=0.00000001; tmp:=1; i:=0; while tmp>e do begin tmp:=x; x:=(a+b)/2; if F(x)*F(a)<0 then b:=x else a:=x; if i<>0 then tmp:=abs(x-tmp) else tmp:=1; i:=i+1; end; edit1.text := floattostr(x); edit2.text := floattostr(F(x)+0.4); edit3.text := floattostr(i); end; Function F(_x:real):real; begin F:=0.14*(1+2*1/2.3*(_x/(2*2.3))*(_x/(2*2.3)))/(1*sqrt(_x)*sqrt(1(_x/2/2.3)*(_x/2/2.3)))-0.4; end; end.