L14-2

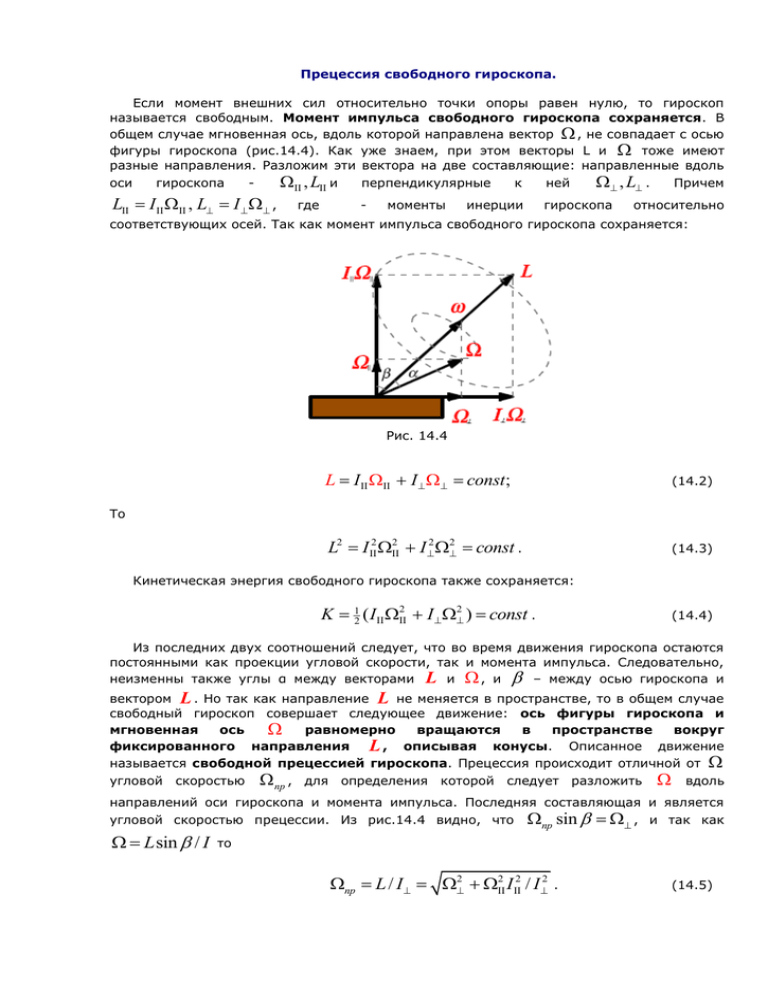
Прецессия свободного гироскопа.
Если момент внешних сил относительно точки опоры равен нулю, то гироскоп
называется свободным. Момент импульса свободного гироскопа сохраняется. В
общем случае мгновенная ось, вдоль которой направлена вектор  , не совпадает с осью
фигуры гироскопа (рис.14.4). Как уже знаем, при этом векторы L и  тоже имеют
разные направления. Разложим эти вектора на две составляющие: направленные вдоль
оси
гироскопа
-
L  I   , L  I    ,
 , L и
где
перпендикулярные
-
моменты
к
ней
инерции
  , L .
гироскопа
Причем
относительно
соответствующих осей. Так как момент импульса свободного гироскопа сохраняется:
Рис. 14.4
L  I    I    const ;
(14.2)
L2  I 2 2  I 2 2  const .
(14.3)
То
Кинетическая энергия свободного гироскопа также сохраняется:
K  12 ( I  2  I  2 )  const .
(14.4)
Из последних двух соотношений следует, что во время движения гироскопа остаются
постоянными как проекции угловой скорости, так и момента импульса. Следовательно,
неизменны также углы α между векторами L и  , и  – между осью гироскопа и
вектором L . Но так как направление L не меняется в пространстве, то в общем случае
свободный гироскоп совершает следующее движение: ось фигуры гироскопа и
мгновенная
ось
 равномерно вращаются в пространстве вокруг
фиксированного направления
L , описывая конусы. Описанное движение
называется свободной прецессией гироскопа. Прецессия происходит отличной от 
угловой скоростью
 пр ,
для определения которой следует разложить

вдоль
направлений оси гироскопа и момента импульса. Последняя составляющая и является
угловой скоростью прецессии. Из рис.14.4 видно, что
  L sin  / I
пр sin    ,
и так как
то
пр  L / I   2  2 I 2 / I 2
.
(14.5)
Гироскопический эффект. Гироскопические силы.
Пусть гироскоп вращается вокруг горизонтальной оси. Если приложить к точкам
пару сил
F, F ,
пытаясь повернуть ось гироскопа вокруг оси
поворачивается вокруг перпендикулярной оси
B, B 
D, D ,
A, A
то она
(рис. 14.5). Это явление называется
гироскопическим эффектом.
Рис. 14.5
Описанное поведение гироскопа полностью объясняется уравнением моментов. Дело
в том, что ось гироскопа является физической осью, по которой направлен вектор
момента импульса. Поэтому изменение ориентации оси гироскопа связано с изменением
вектора L , а последнее описывается уравнением моментов. За элементарный
промежуток времени dt момент импульса гироскопа получает приращение dL = Ldt ,
D, D . Так что через время dt момент
L  t + dt  = L  t   Mdt , который повернут вокруг оси B, B на угол
направленное по моменту пары сил, т.е. вдоль оси
импульса будет
d  Mdt \ L . Вместе с ним поворачивается и ось гироскопа. Заметим, что из-за
гироскопического эффекта ось гироскопа стремится ориентироваться вдоль направления
момента внешних сил, если он имеет фиксированное направление в пространстве. Это и
является физической основой действия гироскопического компаса. Земля, заставляя
всем предметам на ее поверхности участвовать в суточном вращении, действует на них
моментом сил, направленном на север. Поэтому, свободная ось гироскопа на Земле
всегда ориентируется на север. Гирокомпасы широко используются в кораблях, так как
из-за намагниченности их металлических корпусов, магнитные компасы становятся
непригодными.
Рис. 14.6
С гироскопическим эффектом связано появление, так называемых,
гироскопических сил. Если пытаться ось быстровращающего гироскопа со скоростями
v, v повернуть в горизонтальной плоскости (рис.14.6), то он стремится повернуться
вокруг оси
B, B , действуя на руки силами Fгир ,  Fгир . Эти силы, которые, собственно,
называются гироскопическими, всегда перпендикулярны перемещению оси и не
совершают работу. Отсюда и исходит название класса сил, не совершающих работу. С
возникновением гироскопических сил особо считаются в кораблестроении и
самолетостроении, массивные электродвигатели и турбины в которых, фактически
являются гироскопами.
Рис. 14.7
Количественно гироскопические силы могут быть оценены рассмотрением
равномерного качения цилиндрического бегуна на опорную плиту (рис. 14.7). Если
качение катка происходит без скольжения, то угловые скорости связаны соотношением
 r    R,
(14.6)
R и r – длина легкого стержня и радиус катка соответственно. С этими вращениями
связаны соответствующие компоненты момента импульса катка:
L  I   , L  I  .
(14.7)
В процессе движения первая из них остается неизменной, а вторая вращается вокруг
вертикальной оси с угловой скоростью
  . Согласно гироскопическому эффекту, такое
движение оси катка должно привести к появлению гироскопической силы,
увеличивающей давления бегуна на горизонтальную плиту. Вычислим эту силу. За
элементарный промежуток времени dt момент этой силы FRdt приводит к следующему
приросту момента импульса катка:
FRdt  dL  dL  L  dt  I 2
r
dt ,
R
(14.8)
где были учтены две предыдущие формулы. Принимая для катка Iıı = mr2/2, где - ее
масса, окончательно получим
F
mr 3 2 1
  mr  2 .
2
2R
2
(14.9)
Эти силы используются в дисковых мельницах, где они растирают и измельчают
материал, подсыпаемый под каток. При рабочей скорости 1оборот в секунду, т.е. при
   2 рад / с и
r = 50см эта сила равна весу тела и полная сила давления катка на
плиту становится вдвое больше силы тяжести катка:
Fдав  m( g  2 r / 2)  2mg .