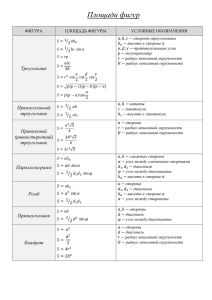
Справочник по геометрии 11 класс. Формулы площадей плоских
реклама
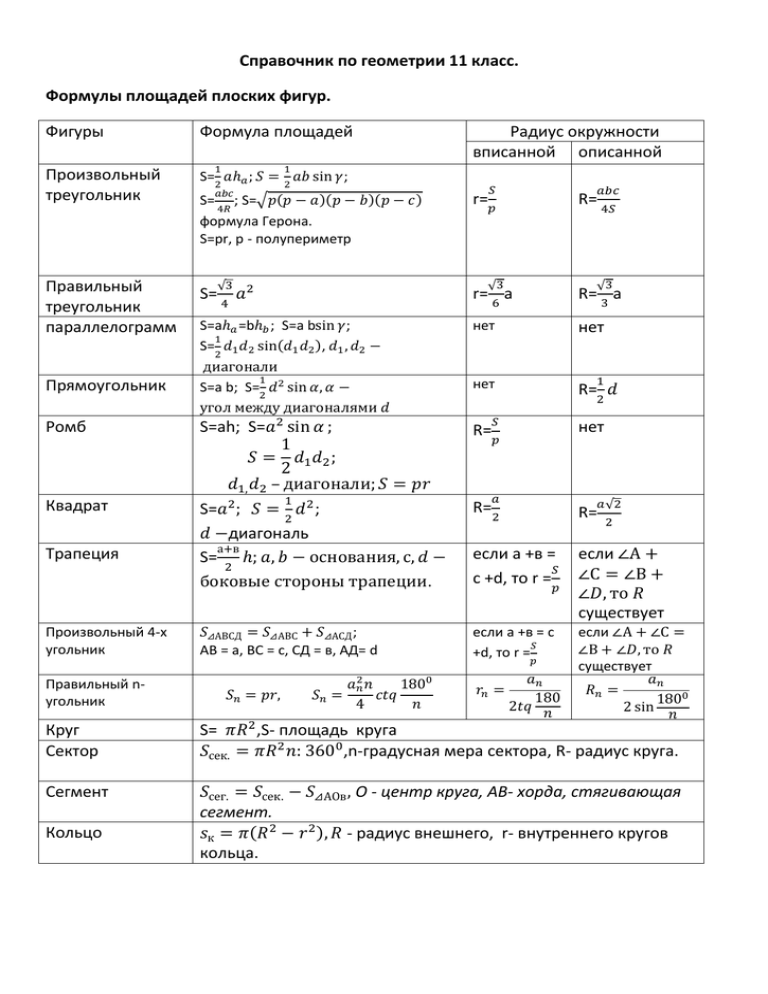
Справочник по геометрии 11 класс. Формулы площадей плоских фигур. Фигуры Формула площадей Произвольный треугольник S=2 𝑎ℎ𝑎 ; 𝑆 = 2 𝑎𝑏 sin 𝛾; Правильный треугольник параллелограмм 1 Радиус окружности вписанной описанной 1 𝑎𝑏𝑐 S= 4𝑅 ; S=√𝑝(𝑝 − 𝑎)(𝑝 − 𝑏)(𝑝 − 𝑐) формула Герона. S=pr, p - полупериметр r= 𝑆 𝑎𝑏𝑐 R= 𝑝 √3 6 √3 2 𝑎 4 4𝑆 √3 3 S= r= a R= a S=aℎ𝑎 =bℎ𝑏 ; S=a bsin 𝛾; 1 S=2 𝑑1 𝑑2 sin(𝑑1 𝑑2 ), 𝑑1 , 𝑑2 − диагонали 1 S=a b; S=2 𝑑2 sin 𝛼, 𝛼 − угол между диагоналями 𝑑 нет нет нет R= 𝑑 Ромб S=аh; S=𝑎2 sin 𝛼 ; 1 𝑆 = 𝑑1 𝑑2 ; 2 𝑑1, 𝑑2 – диагонали; 𝑆 = 𝑝𝑟 R= Квадрат S=𝑎2 ; 𝑆 = 𝑑 2 ; 2 𝑑 −диагональ а+в S= ℎ; 𝑎, 𝑏 − основания, с, 𝑑 − 2 боковые стороны трапеции. R= если а +в = 𝑆 с +d, то r = если ∠А + ∠С = ∠В + ∠𝐷, то 𝑅 существует 𝑆⊿АВСД = 𝑆⊿АВС + 𝑆⊿АСД ; АВ = а, ВС = с, СД = в, АД= d если а +в = с 𝑆 +d, то r =𝑝 если ∠А + ∠С = ∠В + ∠𝐷, то 𝑅 существует 𝑎𝑛 𝑅𝑛 = 1800 2 sin 𝑛 Прямоугольник Трапеция Произвольный 4-х угольник Правильный nугольник 1 𝑆𝑛 = 𝑝𝑟, 𝑎𝑛2 𝑛 1800 𝑆𝑛 = 𝑐𝑡𝑞 4 𝑛 1 2 𝑆 нет 𝑝 𝑎 𝑎 √2 R= 2 𝑝 𝑟𝑛 = 𝑎𝑛 180 2𝑡𝑞 𝑛 2 Круг Сектор S= 𝜋𝑅 2 ,S- площадь круга 𝑆сек. = 𝜋𝑅2 𝑛: 3600 ,n-градусная мера сектора, R- радиус круга. Сегмент 𝑆сег. = 𝑆сек. − 𝑆⊿АОв , О - центр круга, АВ- хорда, стягивающая сегмент. 𝑠к = 𝜋(𝑅2 − 𝑟 2 ), 𝑅 - радиус внешнего, r- внутреннего кругов кольца. Кольцо Справочник по геометрии 11 класс. Формулы для вычисления площадей и поверхностей и объёмов тел. Куб, параллелепипед. S=6𝑎2 V=𝑎3 V= а в с Призма. S – площадь поверхности, V – объём, а – ребро куба. а, в,с–измерения прямоугольного параллелепипеда Sбок. = Росн. H Sбок. = Рсеч. 𝑙 Sбок. = Sосн. 𝑙 V=Sосн. H Росн. − периметр основания, Н − высота Рсеч. − Р перпендикулярного сечения, 𝑙 − боковое ребро. Sосн. − площадь основания, Sсеч. -площадь перпендикулярного сечения. Пирамида. Sбок. = 1/2Росн. ℎ Sбок. = 𝑆/𝑐𝑜𝑠𝜑 V=1/3Sосн. H V=1/3r(𝑆1 + 𝑆2 + ⋯ 𝑆𝑛 + 𝑆осн. ) h- апофема (высота боковой грани) 𝜑 − мера двугранного угла при основании. H − высота. 𝑆1 , 𝑆2 , … 𝑆𝑛 − площади боковых граней. r – радиус сферы, вписанной в пирамиду. Усеченная пирамида. Sбок. = 1/2(Р1+P2 )h. V=1/3H(𝑆1 + 𝑆1 𝑆2 + 𝑆2. ) P1, P2 - периметры оснований,h-апофема. 𝑆1 , 𝑆2 − площадиоснований, H − высота. Цилиндр. 𝑆бок. = 2𝜋𝑅𝐻. S=2𝜋𝑟(𝑟 + 𝐻) V=𝜋𝑟 2 𝐻 Конус. R – основания цилиндра, H − высота, S - площадь полной поверхности. 𝑆бок. = 𝜋𝑅𝑙. S=𝜋𝑅(𝑅 + 𝑙) V=1/3 𝜋𝑅 2 𝐻 Усеченный конус. R - радиус основания, H − высота , l- образующая. 𝑆бок. = 𝜋𝑙 𝑟 + 𝑅 S=𝑆бок. + 𝜋𝑟 2 + 𝜋𝑅 2 V=1/3𝜋𝐻 𝑟 2 + 𝑟𝑅 + 𝑅 2 Сфера. Шар. r, R - радиус основания, H – высота, l- образуюшая. S=4𝜋𝑅 2 S – площадь поверхности, R – радиус шара, V – объём шара. V=4/3𝜋𝑅 3 Шаровой сегмент. Шаровой сектор. S=2𝜋𝑅ℎ V=1/3𝜋ℎ2 3𝑅 − ℎ V=2/3𝜋𝑅 2 ℎ S – площадь поверхности сегмента, R – радиус шара, h –высота сегмента, V- объём сегмента/. R – радиус шара, h –высота сегмента, V- объём сект.