Представление гармонических колебаний
реклама

Лекция 3
Представление гармонических колебаний
и монохроматических волн в комплексном виде
1 i ( t k r )
i ( t k r )
E( r ,t)=acos( t- k r + )=a {
}=
2
e
e
1
i i ( t k r ) 1
i i ( t k r )
= a
+ a
=
2
2
e e
e e
=
Ae
i (t kr )
+
*
i ( t k r )
Ae
1
A 2 ae
i
,
*
A
Ae
=
i ( t kr )
+ к.с.
1 i
a
,
2 e
можно выбрать и:
*
i ( t k r )
Ae
+ к.c.
Комплексная амплитуда у скалярной волны означает наличие начальной фазы и медленно-меняющейся
фазы.
Комплексное число + комплексно сопряжённое = удвоенной действительной части.
Для всех линейных операций (суммирование, интегрирование, вычитание, дифференцирование,
использование граничных условий и т. д., но не умножение и возведение в степень) можно не писать
комплексно сопряженной части (т.е. вместо действительного выражения использовать комплексную запись
для поля E( r ,t))
E( r ,t)=
Ae
i ( t kr )
или E( r ,t)=
*
i ( t k r )
Ae
.
В нелинейной оптике комплексно сопряженная часть обязательно должна записываться, т.к.
используется произведение полей.
Достоинство комплексного представления колебательных и волновых процессов состоит в
простоте обращения с показательной функцией по сравнению с тригонометрическими функциями.
Если в конечном результате отделить действительную часть (удвоив амплитуду) от мнимой, то
получится тот же результат, что и при использовании тригонометрических функций.
Векторный характер электромагнитных волн ( ЭМВ )
( векторные волны )
Поскольку напряженность электрического поля - величина векторная, то и ЭМВ - величина
векторная.
i ( t k r )
E=Ae
Если
.
A - вещественная величина, то это уравнение плоской монохроматической линейно поляризованной
волны. Если
A -комплексная, то поляризация эллиптическая.
1
Поперечность ЭМВ. Ортогональность E и
H.
Рассмотрим плоские волны в диэлектрике:
E = E0
i ( t k r )
e
H H0 e
,
i ( t k r )
Уравнение Максвелла для плоских волн:
i
rot x E
x
Ex
j
y
Ey
k
z
Ez
E z E y
y
z
X
E z ( ik y ) E y ( ik z ) i( E y k z E z k y ) i [ E k ] x
E z E0 z e
i [ t ( k x x k y y k z z )]
.
.
E y E x E z E y E x
rot E i
j
z
z
x k x
y
y
E
div E
z
Ex Ey Ez
Ex
i E k , т.к.
iE x k x
x
y
z
x
и т.д.
Таким образом
rot E i [ E k ]
и
div E i E k , а
Уравнения Максвелла имеют вид:
i [ H k ] i E
c
i [ E k ] i H
c
k
i E k 0
v
c
n
E
i E .
t
i H k 0
[ H n ] i E
c
c
i
[ E n ] i H
c
c
i
n
[ H n ] E
[E n] H
Hn 0
En 0
2
Отсюда следует, что
Итак,
E
и
H n , т.е. перпендикулярны направлению распространения волны.
Таким образом, ЭМВ - волны поперечные.
EH
и взаимно перпендикулярные векторы
n ,E ,H
образуют правовинтовую систему.
E H , т.е. отношение численных значений векторов E
и H от времени
не зависит, т.е. эти векторы обладают одинаковыми фазами.
В бегущей ЭМВ векторы E и H изменяются синхронно.
Энергия, переносимая ЭМВ
Найдем количество энергии, которое протекает в 1 сек через площадку в 1 см 2 , которая
перпендикулярна направлению распространения волны
n.
Для этого построим на площадке
параллелепипед (цилиндр), ось которого параллельна n . Тогда количество энергии, которое протекает
через основание параллелепипеда (цилиндра) в 1 сек, равно энергии содержащейся в части
параллелепипеда (цилиндра) длиной . Следовательно, поток энергии S u v , где u плотность
энергии (энергия в единице объёма).
.
E2 E
u
4
4
c
v
H
EH
4
c
c 2
EH
E ( 1)
4
4
c
S uv n
[E H]
4
S uv
Вектор Умова-Пойтинга
S
совпадает с
n
только в изотропной среде.
c
c
1
E02 cos2 ( t kz )
E02 [ 1 cos 2( t kz )]
4
4
2
c
E 02 .
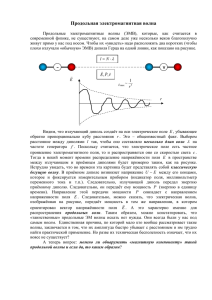
Вектор S изменяется от значения S min 0 до S max
4
S
3
Таким образом, поток энергии колеблется с удвоенной
частотой (по сравнению с
значения
S
E
и H ) около среднего
c
E 02 ,
8
принимая положительные значения (включая S 0 ).
Поток энергии пропорционален квадрату амплитуды
поля ЭМВ. Это общее и очень важное соотношение, на
котором фактически основывается возможность
регистрации
ЭМВ
различными
приёмниками.
Практически все приёмники света в той или иной
степени инерционны. Поэтому они регистрируют
среднее значение квадрата амплитуды поля
(квадратичный детектор).
E02
Световое давление
Поскольку свет электромагнитная поперечная
волна, то падая на поверхность проводника (зеркально отражающего или поглощающего тела), он должен
производить следующие действия: электрический вектор, лежащий в плоскости освещенной поверхности,
вызывает ток в направлении этого вектора
j E,
магнитное поле световой волны действует на возникший ток по закону Ампера (сила Лоренца) так, что
направление действующей силы совпадает с направлением распространения света:
1
Fл [ j H ]Fл‘ [ EH ], Fл‘ S .
c
c
Таким образом, пондермоторное взаимодействие между светом и
отражающим или поглощающим его телом приводит к
возникновению давления на тело. Сила давления зависит от
интенсивности света. Для случая, когда световые лучи образуют
параллельный пучок, давление p по вычислению Максвелла
равняется плотности световой энергии u (тело поглощает всю
энергию, абсолютно чёрное тело)
p u.
Если часть энергии отражается, то давление увеличивается в (1 R)
раз, так как при отражении света, вектор E снова вызывает ток, а
вектор H действует на ток и появляется сила, направленная в ту же сторону (так как при отражении
вектора развернулись)
p u( 1 R ) ,
где R коэффициент отражения тела,
для идеального зеркала
R=1 p=2u.
Примеры
1) Для силы, с которой солнечные лучи в яркий день давят на 1м 2 чёрной поверхности, Максвелл вычислил
величину 0,4 мГ.
4
2) Опыты П. Н. Лебедева (18991900 гг.). Он с точностью порядка 20% измерил величину, рассчитанную
Максвеллом. Он использовал очень чувствительные крутильные весы в сосуде с откаченным воздухом.
Свет воспринимался тонкими и лёгкими крылышками.
3) Оценим давление света от лазерного импульса длительностью u и мощностью Р=1МВт
P u
W P u
,
V S l Sc u
P
Н
к Г
S r 2 , r 1м м, p u 2 10 2 1 2 .
r c
м
м
u
а) разрушение биоткани (опухоли),
б) пондермоторные измерители мощности и энергии лазерных излучателей.
4) Левитация это управление движением малой частицы с помощью лазерного пучка вопреки силе
тяжести.
Расчет сделан для эритроцита.
P
P
F
S c
c
4
4
P
4
3
P r c g
m r 3 r 3 g
3
3
c
3
при r=10 мкм, H O
Р12мВт. Свет полностью
2
F mg F p S u S u
поглощается
частицей. В принципе можно организовать не только удержание, но и
движение частиц
a
F
106 с м 2
с
m
p=1Вт. Лазерный пинцет.
5