Методическая разработка раздела учебной программы

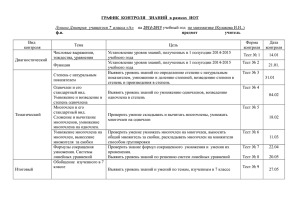
Управление образования и молодежной политики
администрации Городецкого района
Методическая разработка раздела учебной программы
Тема: «Одночлены и многочлены».
ВЫПОЛНИЛ:
Должность: учитель
ФИО: Грошовкина Елена Владимировна
Образование: высшее
Стаж работы в данной должности 17 лет
2013 год
План
1. Пояснительная записка.
2. Цели и задачи раздела.
3. Ожидаемые результаты освоения программы.
4.
Поурочное планирование по разделу.
5. Психолого-педагогическое
объяснение
специфики
восприятия
и
освоение
учебного материала учащимися в соответствии с возрастными особенностями.
6. Обоснование
образовательных
технологий,
деятельности учащихся.
7. Система знаний и система деятельности.
8. Разработка урока.
9. Заключение.
10. Список литературы.
Приложения.
2
методов,
форм
организации
1. Пояснительная записка
Математическое образование в основной школе складывается из нескольких
содержательных компонентов, одним из которых является алгебра. Алгебра нацелена на
формирование математического аппарата для решения задач из математики, смежных
предметов, окружающей реальности. Язык алгебры подчеркивает значение математики
как языка для построения математических моделей, процессов и явлений реального мира.
Одной из основных задач алгебры является развитие алгоритмического мышления,
овладение навыками дедуктивных рассуждений. Преобразование символических форм
вносит свой специфический вклад в развитие воображения, способностей к
математическому творчеству. Формирование у учащихся представлений о роли
математики в развитии общества - вот еще одна из основных задач изучения алгебры.
Данный раздел учебной программы является частью программы основного общего
образования по математике, которая составлена на основе федерального компонента
государственного стандарта основного общего образования.
В данной теме дается определение степени с натуральным показателем. Понятие
стандартного вида числа большего 10 и запись чисел в виде суммы разрядных слагаемых
используются для иллюстрации применения понятия степени с натуральным показателем.
Впервые доказательство теоретического положения в курсе математики проводится при
доказательстве свойств степени, которое осуществляется параллельно с аналогичными
рассуждениями для степеней, основанием которых является число. Особое внимание
следует уделить формированию навыков применения свойств степени с натуральным
показателем в преобразованиях. Так как эти свойства находят применение при умножении
и делении одночленов, возведении одночленов в степень, то основная нагрузка при
закреплении этих навыков ложится именно на материал этого раздела.
Преобразования многочленов играют важную роль в формировании умения выполнять
преобразования алгебраических выражений. Вводится понятие многочлена стандартного
вида. Изучаются алгоритмы сложения, вычитания и умножения многочленов. Важно,
чтобы учащиеся поняли, что при выполнении этих действий над многочленами в
результате получается также многочлен. Деление многочленов и одночленов на одночлен
дается в ознакомительном плане для пропедевтики темы «Алгебраические дроби».
3
2. Цели раздела «Одночлены и многочлены»
Основная цель – выработать умение выполнять действия над степенями с натуральными
показателями, действия сложения, вычитания и умножения многочленов и одночленов.
Развитие
логического
мышления,
алгоритмической
культуры,
математической
критичности мышления и интуиции на уровне, необходимом для дальнейшего обучения.
Овладение устным и письменным математическим языком, математическими знаниями и
умениями по теме необходимыми в повседневной жизни и для продолжения образования.
Воспитание средствами математики культуры личности, отношения к математике как к
части общечеловеческой культуры через знакомство с историей развития понятий
одночлена и многочлена.
Задачи раздела «Одночлены и многочлены»
Обучающие
Сформировать понятие одночлена и многочлена, степени с натуральным показателем,
изучить свойства степени с натуральным показателем, научить применять их при
преобразованиях алгебраических выражений.
Развивающие
Развить представление об алгебраических выражениях и роли их преобразований в
человеческой практике, сформировать практические навыки выполнения устных,
письменных вычислений (вычислительную культуру).
Воспитывающие
Воспитать культуру личности; волю и настойчивость для достижения конечных
результатов при выполнении преобразований выражений.
4
3. Ожидаемые результаты освоения раздела программы.
С этой главы начинается систематическое изучение алгебраических преобразований на
примерах действий со степенями, одночленами и многочленами, которое будет
продолжено во всем курсе алгебры.
Требования к уровню подготовки учащихся.
В результате изучения раздела «Одночлены и многочлены» ученик должен знать и
понимать:
1. Определение степени с натуральным показателем
2. Пять свойств степени с натуральным показателем.
3. Определения одночлена и многочлена, коэффициента одночлена, записывать
одночлены и все члены многочлена в стандартном виде.
4. Алгоритм приведения многочлена к стандартному виду.
5. Алгоритм умножения многочлена на одночлен и многочлен.
6. Алгоритмы деления многочлена на одночлен.
7. Значение практики и вопросов, возникающих в самой математике, для формирования и
развития математической науки.
В результате раздела «Одночлены и многочлены» учащиеся должны уметь:
1. Применять свойства степени с натуральным показателем для преобразования
выражений, в действиях над одночленами и многочленами.
2.
Приводить одночлены и многочлены к стандартному виду, выполнять над ними
действия и соответствующие преобразования.
3. Использовать приобретенные знания и умения в практической деятельности и для
дальнейшего обучения.
5
4. Поурочное планирование по разделу « Одночлены и многочлены ».
Содержание обучения
Степень с натуральным показателем и ее свойства. Одночлен. Многочлен. Сложение,
вычитание и умножение многочленов. Деление одночлена и многочлена на одночлен.
Предлагаемые программы (примерные и авторские) по алгебре составлены в
соответствии
с
требованиями
федерального
компонента
Государственного
образовательного стандарта основного общего образования по математике. Они
позволяют получить полное представление о целях и содержании обучения алгебры в
7-9
классах, в рамках обучения по учебникам, выпускаемым издательством
«Просвещение». Авторские программы составлены в соответствии с требованиями,
предъявляемыми к базовому уровню обучения. При этом авторами программ и учебников
предлагаются
различные
структуры
учебного
материала,
которые
определяют
последовательность изучения материала в рамках стандарта для основной школы и пути
формирования системы знаний и умений, необходимых для применения в практической
деятельности, изучения смежных дисциплин, продолжения образования, а также развития
учащихся.
Планирование темы «Одночлены и многочлены» разными авторскими
коллективами.
Авторы
учебников
Количество
часов
Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др. (после изучения
20
раздела «Уравнения с одним неизвестным»)
А.Г. Мордкович.
Данная тема разбита на 3 главы:
Степень с натуральным показателем.
8
Одночлены. Арифметические операции над одночленами.
9
Многочлены. Арифметические операции над многочленами.
19
Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.И. Суворова.
Данная тема разбита на 2 главы:
Степень с натуральным показателем.
Многочлены.
15
20
6
Г.В. Дорофеев, С.Б. Суворова, Е.А. Бунимович и др.
Данная тема разбита на 2 главы:
Свойства степени с натуральным показателем.
Многочлены.
10
18
Я преподаю в 7-х классах средней общеобразовательной школы. Поурочное планирование
по алгебре 7 класса по разделу
«Одночлены и многочлены» взято мной из книги для
учителя «Изучение алгебры в 7-9классах» (Ю.М. Колягин, Ю.В. Сидоров, М.В. Ткачев и
др./М.Просвещение, 2002) вариант 1 (3 часа в неделю, всего 102 часа) по учебнику
Алгебра, 7 класс (учебник для общеобразовательных учреждений / Ш.А. Алимов,
Ю.М Колягин., Ю.В. Сидоров и др. / М. Просвещение, 2002 г).
Поурочное планирование по разделу « Одночлены и многочлены ».
Номер
пункта
Содержание материала
Количество
часов
Глава III. Одночлены и многочлены.
20
18-19
Степень с натуральным показателем. §9.
2
20-22
Свойства степени с натуральным показателем. §10.
3
Одночлен. Стандартный вид одночлена. §11.
1
Умножение одночленов. §12.
2
26
Многочлены. §13.
1
27
Приведение подобных членов. §14.
1
28-29
Сложение и вычитание многочленов. §15.
2
30
Умножение многочлена на одночлен. §16.
1
31-33
Умножение многочлена на многочлен. §17.
3
34-35
Деление многочлена и одночлена на одночлен. §18.
2
36
Обобщающий урок.
1
37
Контрольная работа №3.
1
23
24-25
7
5. Психолого-педагогическое объяснение специфики восприятия и освоения
учебного материала учащимися в соответствии с возрастными особенностями.
В настоящее время наблюдается усиленный интерес учителей математики к
психолого–педагогическим проблемам, к психологическим знаниям. Этот интерес
обусловлен тем, что учителя математики в своей повседневной
практической
деятельности встречаются с такими проблемами, которые можно разрешить лишь на
основе
психолого–педагогических
знаний,
а
также
при
условии
глубокого
психологического осмысления сущности этих проблем.
1. Ученик как объект и субъект процесса обучения.
В процессе обучения математике непосредственно участвуют с одной стороны— учитель,
с другой — ученик. Роли их в этом процессе представляются, по крайней мере на первый
взгляд, достаточно ясными: учитель организует, направляет и руководит процессом
обучения математике, а ученик должен учиться, выполнять все требования учителя.
Вот как, например, определяется процесс обучения в одном из учебников по педагогике:
«Обучением называется двусторонний процесс, состоящий из деятельности учителя, когда
он ученикам объясняет, рассказывает, показывает, заставляет их выполнять упражнения,
исправляет их ошибки и т.д., и из деятельности учеников, которые под руководством
учителя усваивают знания и соответствующие умения и навыки».
Основная роль учителя математики в современных условиях — это воспитание личности
учащихся, формирование их потребностно–мотивационной сферы, воспитание их
способностей, нравственных идеалов и убеждений. Обучение знаниям умениям и навыкам
по математике является составной частью этого воспитания и тем процессом, в котором
это воспитание осуществляется.
2. Возрастные психологические особенности ученика как объекта обучения
математике.
О том, что надо учитывать возрастные особенности учащихся, говорится всюду, но не
всегда указывается, что это означает, какие особенности надо учитывать и как их надо
учитывать.
Подростковый возраст — это весьма сложный, таящий в себе опасность кризисных
явлений, период в жизни ученика. Подросток становится более независимым от взрослых
8
ещё и потому, что у него возникают такие потребности, которые он должен удовлетворить
только сам, и это зачастую болезненно сказывается на отношении учащихся к учению.
Вот как характеризует это известный психолог Н.С. Лейтес: «Дети 12–13 лет в
подавляющем большинстве своём относятся к учению в основном благодушно: не
утруждают себя излишними раздумьями, выполняют только уроки в пределах заданного,
часто находят поводы для развлечения… Ослабление связи с учителем, снижение его
влияния особенно дают о себе знать в недостатках поведения учеников на уроках. Теперь
учащихся не только иногда позволяют себе игнорировать получаемые замечания, но
могут и активно им противостоять. В средних классах можно столкнуться с
изобретательными шалостями и проявлением самого легкомысленного поведения».
Знания ученика будут прочными, если они приобретены не одной памятью, не заучены
механически, а являются продуктом собственных размышлений и закрепились в
результате его собственной творческой деятельности над учебным материалом.
Самостоятельное проникновение в новые области знания, преодоление трудностей
вызывает чувство удовлетворения, гордости, успеха, т.е. создает тот эмоциональный фон,
который характерен для интереса.
Принято различать три группы условий, стимулирующих развитие познавательных
интересов: первая группа условий связана с содержанием учебного материала, вторая с
организацией
процесса
обучения
и
третья
группа
определяется
отношениями,
складывающимися между учениками и учителем.
К первой группе условий относится новизна содержания, обновление уже усвоенных
фактов, исторический подход к сообщаемому материалу, раскрытие практического
значения знаний и показ современных достижений науки.
Ко второй группе в педагогике принято относить такие методы преподавания, как
разнообразные формы самостоятельной работы, проблемное обучение, исследовательский
подход к изучаемому материалу, творческие и практические работы учащихся.
К третьей группе относят способности учащихся, увлеченность преподаванием самого
учителя, его готовность прийти на помощь ученикам, вера в их силы и возможности,
требовательность и справедливость, поощрения, взаимопомощь учащихся.
Известно, что знания и умения связаны между собой. Умение определяется как
способность личности к эффективному выполнению определенной деятельности на
основе имеющихся знаний в измененных или новых условиях. Умение характеризуется,
прежде всего, способностью с помощью знаний осмысливать имеющуюся информацию.
Невозможно добиться глубины и прочности знаний, если не заниматься формированием
умений.
9
Главные составляющие успешного учительского труда – это отлично владеть своим
предметом, глубоко знать содержание преподаваемого курса, применять современные
педагогические технологии в образовательном процессе.
Первым вопросом, который возникает в связи с задачей использования условий
формирования математических интересов на уроках, является вопрос о их содержании.
Это содержание определяется программой и школьными учебниками, вместе с тем, оно
постоянно обогащается учителем.
Вторым вопросом является вопрос об организации, структуре и методах проведения
урока.
Разнообразие системы уроков должно привести к тому, что ученики будут с нетерпением
ожидать каждый урок математики и будут досадовать, что он уже кончился. Учащимся
нравится увлекательное преподавание, под которым они понимают преподавание,
характеризующееся достаточно быстрым темпом, ясностью изложения материала и
воодушевлением самого учителя. Личность учителя для формирования интереса к
изучению математики играет очень большую роль, причем наиболее важной чертой в
этом является его увлеченность предметом и преподаванием, желание учителя поверить в
возможности ученика, готовность прийти ему на помощь. Очень благотворно влияет на
формирование интереса поощрение учителя. Отметка, выставляемая в журнал, есть лишь
выражение поощрения, гораздо большее значение имеет похвала учителя, слова,
сказанные при этом.
10
6. Обоснование используемых в образовательном процессе по разделу
«Одночлены и многочлены» программы образовательных технологий, методов,
форм организации деятельности учащихся.
В главе «Одночлены и многочлены» рассматриваются следующие дидактические
единицы.
Определения (термины, символы): степени с натуральным показателем (степень,
показатель степени, основание степени), стандартного вида числа, одночлена,
стандартного вида одночлена, коэффициента одночлена, подобных одночленов,
многочлена, стандартного вида многочлена.
Теоремы: свойства степени с натуральным показателем.
Алгоритмы: представления одночлена и многочлена в стандартном виде, умножения
многочлена на одночлен, умножения многочлена на многочлен, деления многочлена на
одночлен.
Ключевые задачи: найти значение выражения, записать выражение в виде степени с
заданным основанием (применяя свойства степени), упростить выражение, найти
произведение многочлена и одночлена, выполнить умножение многочленов.
Материал данного раздела можно разбить на три основных блока: «Степень»,
«Одночлены», «Многочлены»
Блок 1. «Степень».
§9. Степень с натуральным показателем (2 ч).
§10. Свойства степени с натуральным показателем (3 часа).
Цель изучения параграфов– знакомство учащихся с определением степени с натуральным
показателем и обучение вычислению степени числа, а также записи числа в стандартном
виде; формирование начальных умений в применении свойств степени с натуральным
показателем для преобразований числовых и алгебраических выражений, а также для
упрощения выражений.
Так как учащиеся впервые сталкиваются с понятием степени ( с показателем больше 3), то
начать первый урок по данной теме можно следующим образом:
«В Древней Индии была такая легенда. Стоит камень размером в кубический километр, в
миллион раз тверже алмаза. Один раз в миллион лет к нему прилетает птичка и трется
клювом о камень. В конце концов в результате этого камень износится. Как вы думаете,
сколько лет понадобится для того, чтобы камень износился до основания? Вычисления
математиков показывают, что для этого понадобится 1035 лет.
11
1. Почему именно эта запись здесь применена? (В записи числа будет 35 нулей и
словесно это число иначе произнести нельзя).
2. Что собой представляет данное число? (Степень, основание – 10, показатель - 35).
Таким образом, показатель степени помогает нам упростить запись произведения
одинаковых множителей».
Далее вводится определение степени с натуральным показателем.
Определение степени числа a с натуральным показателем n должно быть хорошо изучены
учащимися, т.к. на его основе вырабатывается алгоритм вычисления степени, поэтому для
лучшего запоминания определения степени с показателем n, большим 1, и n=1, а также
названий компонентов степени я на все время изучения главы помещаю перед учащимися
плакат и раздаю памятки следующего содержания ( принцип наглядности) :
Степень с натуральным показателем
Определения
1.
n
a
Обозначения
степень
 a  a  a  a  ...  a
a
n раз
2.
1
a
n
показатель степени
a
основание степени
3.
n
0
0
При выполнении упражнений на уроке требую от учащихся грамотного прочтения
выражений вида a
n
при конкретных значениях a и n.
Так же считаю целесообразным наличие у учащихся таблицы степеней чисел 2 и 3, что
способствует лучшему запоминанию и «узнаванию» нужных чисел при выполнении
заданий.
n
2n
3n
1
2
3
2
4
9
3
8
27
4
16
81
5
32
243
6
64
729
7
128
2186
8
9
256
512
6561 19683
10
1024
59049
При рассмотрении примеров на вычисление значения степени следует помочь учащимся
понять, как найти знак степени при возведении в степень отрицательных чисел; показать,
что формула (-a)² = -a² неверна и предостеречь учеников от возможных ошибок.
Как один из вариантов устного счета можно предложить следующий.
12
Представьте 64 в виде степени с основанием 2; -2; -8. Куб какого числа равен 64?
Существует ли еще какой-нибудь способ представления 64 в виде степени с натуральным
показателем? Если да, то назовите его.
б) Вычислите значение выражения ( можно использовать и как самостоятельную работу)
а)
а)
б)
б)
в)
в)
г)
г)
,
в). Подчеркни неравенства в которых верно выполнено сравнение степеней.
1)
(-4)2 < (-4)3
2)
(-6,2)4 > 0
3)
(-3,5)5 > 0
4)
(-2)3 = -23
г). Покажите с помощью стрелки, равно ли значение выражения нулю, положительному
числу или отрицательному:
13
Вариант 1
Вариант 2
На последнем уроке при изучении параграфа провожу самостоятельную работу
следующего содержания:
1.Вычислить:
1). 6² ; 2). (2)
5
1
; 3). (1 )
2
2
1
; 4).  ( )
2
4
; 5). (2)
4
; 6). (3)
3
 (2)
2
 (0,2)
2
.
2.Упростить выражение:
1). y  y  y  7  7  7  7 ; 2). (3a)  (3a)  (3a)  n  n  n  n  m ; 3). (a  b)  (a  b)  (a  b) .
3. Записать частное квадратов чисел х и у.
К концу изучения §9 все учащиеся должны знать определение степени с натуральным
показателем.
При изучении материала §10 учащиеся впервые в явном виде встречаются на уроках
алгебры с теоремами и их доказательствами в явном виде. Поэтому каждому ученику
после доказательства свойств степени раздаются обучающие карты (приложение 1). В
14
учебнике достаточно большой выбор заданий, соответствующих принципам
однотипности, полноты и вариативности, но для разнообразия форм работы с учениками
можно предложить следующие задания.
1. Соедини линиями выражения, соответствующие друг другу.
3235
35:32
32*5
25:35
(23)5
32+5
(32)5
2535
2
 
3
5
35-2
2. Найди выражения, в которых допущены ошибки и отметь их галочкой.
1) 24 = 16
2) 53 = 15
3) -81 = (-3)4
4) (-4х)3 = -64х3
3. Карта для устного счета.
1). Упростите выражения:
1
2
3
4
5
6
7
d5d7
d5d8
d5d10
d6d7
d6d8
d5d9
d6d9
(-b)2b2
(-b)2b
(-b)2b3
(-b)2b4
(-b)3b
(-b)3b2
(-b)3b3
-b3b2
-b3b
-b3b3
-b3b4
-b4b
-b4b2
-b4b3
x5x3x2
x5x3x3
x5x3x4
x5xx
x5x4x
xx3x
x2xx
(x3)2
(x3)3
(x3)4
(x3)5
(x2)2
(x2)3
(x2)4
(-y2)3
(-y5)2
(-y5)3
(-y15)3
(-y15)2
(-y5)4
(-y4)2
((-x)2)5
((-x)2)3
((-x)2)4
((-x)3)2
((-x)3)3
((-x)4)2
((-x)4)3
15
dkd3d4
d7dkd4
dkd2d
dnd2d5
dkd3d6
dkd9d
d5dnd7
d3(d3)2
d(d2)3
d3(d2)3
d3(d4)5
d2(d3)2
d(d5)2
d2(d3)4
(d2d4)2
(dd2)3
(d2d)2
(d3d5)2
(dd3)5
(d3d3)3
(dd5)4
pkp2
pkp
p3pk
p4p2k
pk3pk
p3p2k
ppk
(cd)3
(cd)4
(cd)5
(cd)6
(c2d)2
(c3d3)2
(c4d)3
x17 : x9
x3: x
x8 : x3
x15 : x
x3 : x3
x7 : x3
x11 : x8
c4 : c3
c11 : c8
c6 : c5
c8 : c
c18 : c8
c7: c
c19 : c19
2) . Представьте в виде степени выражения :
1
2
3
4
5
6
7
58*25
57*25
56*25
55*25
54*25
53*25
52*25
312*27
311*27
310*27
39*27
38*27
37*27
36*27
615*36
614*36
613*36
612*36
611*36
610*36
69*36
32*29
32*28
32*27
32*26
32*25
32*24
32*23
56 : 54
57 : 54
58 : 54
59 : 54
56 : 53
57 : 53
58 : 53
81*36
81*37
81*38
81*39
81*310
81*311
81*312
Так как учащихся в скором времени ждет государственная итоговая аттестация, то
необходимо уже с 7 класса приучать учащихся к заданиям в тестовой форме. Тестовые
задания удобно использовать при организации самостоятельной работы учащихся в
режиме самоконтроля, при повторении учебного материала и как итоговый контроль
знаний. Тексты тестов приведены в приложении 2.
В результате изучения §10 все учащиеся должны знать пять свойств степени и уметь их
применять.
Блок 2. «Одночлены».
§11. Одночлен. Стандартный вид одночлена (1час).
§12.Умножение одночленов (2 часа).
Цель изучения параграфов - введение понятия одночлена и обучение приведению
одночлена к стандартному виду, знакомство учащихся с умножением одночленов.
Учащиеся узнают, что произведение числовых и буквенных множителей (неоднократно
встречающееся ранее алгебраическое выражение), называется одночленом; что такое
16
коэффициент одночлена и как найти произведение одночленов. Важно, чтобы учащиеся
поняли, что в одночлене не должно быть операций сложения, вычитания и деления.
В качестве устной работы предлагаю учащимся задания такого плана, например:
1. Из данных выражений (они записаны на доске заранее) выбрать одночлены и заполнить
таблицу:
- 5x2 7yx; a+3b3 · b2; aabbb; -x3; 2 ab+c-4; (-1/4)2bab3;
a  b 2a
2
;
;
.
4
 3  3a
Одночлен Его стандартный вид Коэффициент
1.
2. Найди ошибку.
а).
;
б).
.
3. “Стрела”. Найдите произведение выражений и результат запишите в третий
прямоугольник. Найдите произведение двух последующих выражений и запишите
результат в следующий прямоугольник и т.д. Какое выражение будет записано в седьмой
клетке.
2a
2
3b
3
4. Запишите в клетки каждого квадрата такие выражения, чтобы их произведение в
каждой строке и в каждой диагонали была равна магическому выражению, записанному в
треугольнике.
12
x
x
2
x
x
3
4
17
После изучения данных параграфов предлагаю учащимся разноуровневую
самостоятельную работу.
Вариант № 1
1.(на оценку 3) Выполните умножение:
а) 4а * 8b
б) – 10а * (–5а2)
в) – 0,1b * (–10b3)
г) a2b6 * (–2ab)
д) 0,2x2y * (–5xy2)
е) 1/3 a3b4 * (–1/5a2b)
2. (на оценку 4) Преобразуйте выражение в одночлен.
а) 5ab * 0,7b2c
б) – 1/4 ad * (–4a3d4)
в) – 16abc * (–0,5cb2)
г) – a3b * 3a2b4 * (–ab)
д) (–1/4a3b4c3)3
е) (–0,2xy4)4
3.(на оценку 5) Преобразуйте выражение в одночлен стандартного вида.
а) (xy)3 * (–3x4y2)
б) 0,5a2b3 * (–2b)6
в) (0,2m2n)3 * 1000m4n7
г) –7c8 * (–0,4c3)2
д) (1/4m2n)3 * (–32m9n)
е) (–2xy4)2 * (–27x3y)
При наличии времени или в качестве домашнего задания можно предложить тесты по
результатам усвоения §9,§10,§11 (приложение 3).
В результате изучения параграфов учащиеся должны уметь выявлять одночлены,
записанные в стандартном виде, определять коэффициент одночлена, уметь выполнять
умножение одночленов и возведение одночленов в степень.
Блок 3. «Многочлены»
§13.Многочлены (1 час). §14.Приведение подобных членов (1 час).
§15. Сложение и вычитание многочленов (2часа). §16. Умножение многочлена на
одночлен (1час). §17. Умножение многочлена на многочлен (3часа). §18. Деление
многочлена на одночлен (2 часа).
Цель изучения §13, §14 – введение понятия многочлена как алгебраической суммы
одночленов, знакомство с одним из важнейших алгебраических преобразований приведением подобных слагаемых.
В начале урока повторяю с учащимися понятие алгебраической суммы, алгоритм
приведения одночлена к стандартному виду, правила умножения рациональных чисел в
ходе устной работы. Изучение новой темы предлагаю учащимся провести самостоятельно,
18
после чего учащиеся отвечают на поставленные вопросы и записывают в тетради и на
доске примеры многочленов. После работы с номерами из учебника при наличии времени
провожу самостоятельную работу.
При введении понятия подобных членов следует обратить особое внимание на то, что при
приведении подобных членов буквенные множители остаются неизменными, отработать
приведение подобных членов с противоположными коэффициентами. Как один из
вариантов самостоятельной работы можно предложить следующий:
1. Из записанных одночленов выбрать подобные и найти их сумму:
2
32 х ² у ²; 4a
b ; 10 xy ; 13ab
2
;  10 xy ;
-8 а²b; -8 аb; - 8а b; 9 х ²у ²; 27 х ²у ²; -13 а b²
2. Представьте в стандартном виде многочлен 3а – 5а∙а – 5 + 2а2 – 5а +3.
1) ─ 3а² – 2а – 2
3) ─ 3а² – 8а – 2
2) ─5а³ – 2
4) 2а² – 7а – 2
3.Записать во втором столбце такой одночлен, чтобы его сумма с соответствующим
одночленом из первого была равна одночлену, записанному в третьем столбце.
5 a² b³
 18a
5
b
13 a ²b³
7
0
2,4 x
7,4 p q
6st
0
4
3
yz
4pq
 1,2 st
4
После изучения материала этих параграфов все учащиеся должны знать определение
многочлена, называть члены многочлена, уметь записывать все члены многочлена в
стандартном виде, знать и уметь применять алгоритм приведения многочлена к
стандартному виду.
Целью изучения параграфа «Сложение и вычитание многочленов» является
формирование умения приводить сумму и разность многочленов к многочлену
стандартного вида. Так учащиеся знают правила раскрытия скобок, то алгоритм сложения
19
и вычитания многочленов особой трудности не вызывает, при этом учащиеся должны
проговаривать выполняемые действия. Для проверки знаний учащимся предлагаю
опорный тест теоретического материала по теме: «Сложение и вычитание многочленов», а
также разноуровневую самостоятельную работу (приложение 4).
Целью изучения следующих параграфов - знакомство учащихся с алгоритмами
умножения многочлена на одночлен, умножения многочлена на многочлен, деления
многочлена на одночлен и формирование умений в их применении.
Умножение многочлена на одночлен основано на знакомом учащимся распределительном
свойстве умножения, поэтому у большинства учеников данное действие не вызывает
затруднений. Более слабым учащимся рекомендую следующую запись, например:
7ав (2а + 3в) = 7 2 аав + 7 3 авв = 14а ²в + 21 ав ².
(Разработку урока «Умножение многочлена на одночлен» см. далее).
При умножении многочлена на многочлен учащиеся также применяют аналогичную
запись, которая помогает учащимся умножать каждый член одного многочлена на каждый
член другого многочлена. При выполнении заданий стараюсь требовать от учащихся
проговаривать заданные алгебраические выражения и выражения, полученные в
результате умножения. В качестве контроля усвоения материала данных параграфов
предлагаю учащимся задания в тестовой форме (приложение 5).
Материал последнего параграфа данного раздела помогает сформировать у учащихся
более полные представления о действиях над алгебраическими выражениями и в
дальнейшем осознанно выполнять разложение многочлена на множители.
При делении многочлена на одночлен следует обратить внимание учащихся на количество
членов в многочлене-частном, их должно быть столько же, сколько в многочленеделимом - это предупреждает ошибки с потерей 1 (или -1) в частном. Зафиксировать
сказанное можно в ходе решения уравнений вида:
1). (3х³ + 2х² – х) : х = 3х (х – 2);
2). 4х (х+1) = (8х³ – 4х² + 2х) : 2х.
Как один из вариантов самостоятельной работы предлагаю следующий:
1. Выполнить умножение, а затем деление выражений:
1). (-0,25аb²с) и 5аbс; 2). (7m² – 20mn – 10m) и 10m .
2. Упростить выражение (14 x
4
 7x
3
)  7x
1
выражение при x  1 .
6
20
3
 4 x и найти его числовое
В результате изучения этих параграфов учащиеся должны знать алгоритмы умножения
многочлена на одночлен и многочлен, деления многочлена на одночлен и уметь их
применять при преобразовании выражений и решении уравнений.
21
7. Система знаний и система деятельности.
Линия темы «Одночлены и многочлены» в обучении детей алгебре очень важна. При
изучении данной темы формируются основные знания, умения и навыки работы с
алгебраическими выражениями, которые необходимы для изучения всего курса алгебры.
Фундаментальные знания по теме раздела включают в себя следующие понятия:
определения степени с натуральным показателем, одночлена, многочлена, алгоритмы
совместных действий над одночленами и многочленами.
Система деятельности включает:
1. познавательная деятельность: а) интеллектуальные мыслительные операции (анализ,
обобщение, аналогия); б) наблюдение и постановка проблемы (как выполнить указанные
действия).
2. преобразующая деятельность: способы поиска путей преобразования выражений.
3. Общеучебная деятельность включает в себя следующие методы учения: организация
учебного места, способы поиска информации, работа с литературой (учебником,
подготовка докладов, например, по теме «Кто первый ввел понятия одночлена и
многочлена», составление кроссвордов); навыки общения (монолог, диалог, способы
слушать и задавать вопросы); методы взаимообучения : организация работы в группе (на
примере разработанного урока), взаимопроверка и взаимооценка.
4. Самоорганизующая
деятельность: самостоятельная постановка целей и техника
планирования (при выполнении тренажёров, тестов), самоконтроль.
22
8. Разработка
урока.
Первый урок по теме «Умножение многочлена на одночлен» в 7 классе.
Тип урока: урок изучения нового.
Цель урока: вывести алгоритм умножения одночлена на многочлен.
Задачи урока:
обучающие: отработка правила умножения многочлена на одночлен и приведения
многочлена к стандартному виду;
развивающие: обеспечение возможности каждому учащимся достичь определенного
уровня, развитие математической речи учащихся, формирование умения обобщать,
систематизировать, развитие навыков самоконтроля;
воспитательные: воспитание умения слушать, воспитание воли и настойчивости для
достижения конечных результатов при умножении многочлена на одночлен, умения
работать в группах.
Знания и навыки учащихся: научиться применять алгоритм умножения многочлена на
одночлен.
Оборудование: мультимедийный проектор, раздаточный материал.
Предварительная подготовка класса: класс разбит на три группы равных учебных
возможностей.
План урока:
1.Организационный момент.
2.Открытие новых знаний.
3. Формирование умений и навыков.
4. Контрольные вопросы.
5. Рефлексия.
6. Домашнее задание.
Ход урока
I. Организационный момент.
Учитель: Сегодня на уроке вы будете работать в группах. Для совместной работы нужна
взаимовыручка, взаимоподдержка, умение слушать друг друга, умение принять точку
зрения другого. Надеюсь, ваша совместная работа, сегодня на уроке, будет именно такой.
II. Открытие новых знаний.
На доске записаны следующие выражения:
23







(1 + 3а)+(а2 - 2а);
(2х2 + 3х) – (-х + 4);
(в2 + в -1) – (в2- в +1);
18х2 – (10х – 5 + 18х2);
2х(х2-7х-3);
2а(3а – 5);
-4в2(5в2-3в +1)
Учитель: Посмотрите на выражения, записанные на доске. Что вы можете сказать о них?
Что это за выражения? (Одночлены и многочлены.)
- Какое задания вы могли бы предложить к ним? (Сложить и вычесть многочлены,
умножить одночлен на многочлен.)
- Какие задания вы с легкостью бы выполнили? (Сложить и вычесть многочленывыполняютзадания.)
- Какие задания вы не сможете выполнить? (Умножить одночлен на многочлен.)
- ИТАК, какую учебную задачу поставим на урок? (Научиться умножать одночлен на
многочлен.)
- А что значит научиться? (Вывести правило или алгоритм умножения одночлена на
многочлен).
- Т.е. мы должны разработать алгоритм умножения одночлена на многочлен. (Слайд 1тема урока, приложение 6).
- Какую учебную цель мы поставим на урок? (Разработать алгоритм умножения
одночлена на многочлен.) (Слайд 2).
- Какие знания нам понадобятся для этого? (Распределительный закон умножения,
правила раскрытия скобок.)
- Кто пойдет к доске? Кто готов выбрать одно из предложенных выражений и попробовать
умножить одночлен на многочлен?
- Остальные могут выбрать другое выражение и разобрать его самостоятельно.
Пример: 2х (х2 – 7х – 3) = 2х · х2 – 2х · 7х – 2х·3 = 2х3 -14х2 – 6х
- Какой первый шаг нашего алгоритма?
24
(Слайд 3).
- Какой второй шаг алгоритма?
(Слайд 3).
- И, наконец?
(Слайд 3).
- Еще раз повторим алгоритм умножения одночлен на многочлен. (Слайд 4).
- Мы справились с учебной задачей?
- Что же еще нам осталось сделать? (Потренироваться.)
III. Формирование умений и навыков.
Учитель: Как вы думаете, что это у вас в конвертах? (Учитель показывает на карточки –
элементы схемы алгоритма).
Работа по группам.
1) Учитель: В каждой группе имеется набор таких же карточек – элементов схемы.
Разложите схему умножение одночлена на многочлен, так, как вы ее
представляете.(Учитель смотрит, какие схемы получились у ребят в группах)
25
Учитель: Сравните схему, которая получилось у вас в группах и ту, которая получилось
на доске! (Слайд 5)
Учащиеся сравнивают свою схему со схемой на экране.
2) Учитель: А теперь впишите свои пример умножения одночлена на многочлен в свою
схему.
Учащиеся придумывают и вписывают свои примеры умножения одночлена на многочлен
в свои схемы.
Учитель: Проверьте друг друга.
- Какой результат получился у первой группы? (Учащиеся отвечают.)
- А у второй? (Учащиеся отвечают).
И так далее.
Учитель: Мы составили одну схему. Каждая группа придумала свой пример, применила
один и тот же алгоритм и справилась с заданием.
- Какой же вывод можно сделать?
- Алгоритм действует только для одного выражения? (Для разных выражений).
3) Учитель: А сейчас я предлагаю вам задание: найти в предложенных решениях ошибки
и обосновать их, провести исследования этих решений.
Каждая группа получает листы с заданием.
Задание для 1-й группы. (Слайд 6).
26
Задание для 2-й группы. (Слайд 6).
Задание для 3-й группы. (Слайд 6).
Если группа находит ошибку, обводит ее красным карандашом. Затем от каждой группы
выходит представитель и поясняет где, по их мнению, нарушен алгоритм.
Учитель: Как вы думаете, будет ли действовать этот алгоритм для данных выражений?
(Учитель открывает доску, на которой записаны выражения).



(а + в) (с + d)
(х + у) (х – у)
(z – 1)(z – 2)
- Попробуйте поработать с ними, применить данный алгоритм. Это будет частью вашего
домашнего задания.
4) Задание. Составьте из карточек красного и зеленого цвета верные равенства.
(Для быстрой самопроверки на обратной стороне карточек, соответствующие пары
обозначены одинаковыми значками
).
IV. Контрольные вопросы.
27
1) Как умножить одночлен на многочлен? Приведите пример.
2) Какое свойство умножения используется при умножении одночлена на многочлен?
3) Ученик умножил одночлен на многочлен, после чего одночлен оказался стертым.
Восстановите его.
… (х - у) = 3ах – 3ау
… (2а + в) = 2а2 + ав
… (х – у2 + 1) = ху2 – у4 + у2
V. Рефлексия.
Каждой группе выдаётся лист с вопросами.
Попробуйте оценить свою работу по 10-бальной шкале.
Как работала группа:



дружно, совместно разбирали задания – 9-10 б;
не все активно участвовали в обсуждении – 7-8 б;
работа была вялая, неинтересная, много ошибок – 4-6 б.
Сформулируйте Ваше мнение об уроке. Ваши пожелания. Что понравилось?
После обсуждения в группах представитель от каждой группы зачитывает пожелания
перед всем классом.
Учитель: Сегодня на уроке вы работали группой. И, надеюсь, убедились, вместе работать
легче, вместе – интереснее. И как бы ни был труден путь к знаниям, вместе его преодолеть
легче!!!
VI. Домашнее задание (заранее заготовлено и распечатано на листах каждому ученику).
Учитель: Объем домашнего задания каждый выберет сам. Вы можете выполнить все
задания и получить оценку «5», можете выполнить задания 1-4 и получить оценку «4», а
кому достаточно минимальной оценки выполняют задания 1-3.
Домашнее задание
1. Раскройте скобки:
а) с (2а + b)
б) 2а (3b + 5)
в) – а (b + 3)
г) -1 · (4m + 7)
2. Представьте в виде многочлена:
а) 5 (а2 – 2аb + b2)
б) 2 (m2 -3m + 3)
28
3.
4.
5.
6.
в) -3 (х2 + ху + у2)
г) -4 (1 - 2n2 – 3n3)
Упростите выражение:
а) 3n2 – n (4n – 6m)
б) 5а + 2а (3а – 2)
Упростите выражение:
а) а (а + b) – b (a – b)
б) 2х (х – у) – у (у- 2х)
Упростите:
а) 2 р (1- р – 3р2) – 3р (2 – р – 2р2)
б) 2с (5а – 3с2)- с (а – 6с2) + 3а (а – с)
Представьте произведение в виде многочлена:
а) (х + 3) (х + 1)
б) (с + 8) (с + 2)
29
9. Заключение.
Тема моей работы «Одночлены и многочлены». Работая по данной теме, я изучила
теоретический материал, методику преподавания математики с учетом возрастных
особенностей подростков, постаралась систематизировать методы и приемы, помогающие
научно и доступно преподнести сложный материал. Новизна, необычность,
неожиданность, странность, несоответствие ранее изученному, все эти особенности,
подчеркнутые при сообщении материала, способны не только вызвать мгновенный
интерес, но и пробудить эмоции, порождающие желание изучить материал более глубоко,
то есть содействовать устойчивости интереса.
Думаю, что предложенные задания при разработке данного раздела способствуют
пробуждению интереса учащихся , так как дети активно работали, с энтузиазмом
выполняли предложенные задания, включались в различные виды деятельности,
выполняли творческие задания.
При работе с учащимися стараюсь найти индивидуальный подход к каждому, учитываю
способности каждого ребенка, уважаю ученика, как личность.
30
Список литературы.
1. Алгебра: учебник для 7 класса общеобразовательных учреждений / Ш.А, Алимов
Ю.М. Колягин, Ю.В. Сидоров, Н.Е. Федорова, М.И. Шабунин, 10-е издание-М:
Просвещение,2002.
2. Программы общеобразовательных учреждений
Алгебра 7-9 классы / Т.А. Бурмистрова – М.: Просвещение 2009.
3. Изучение алгебры в 7-9 классах: Кн. Для учителя / Ю.М. Колягин, Ю.В. Сидоров,
М.В. Ткачева и др. - М. Просвещение, 2002.
4. Теоретические основы обучения математике в средней школе. / Учебное пособие под
редакцией Т.А. Ивановой - Нижний Новгород, 2003.
5. Учебно–методическая газета «Математика», №4, 2004.
6. Дидактические материалы по алгебре 7 класс / Л.И. Звавич, Л.В. Кузнецова, С.Б.
Суворова – М. Просвещение, 1991.
7. Методика преподавания математики в средней школе./ Ю.М. Колягин, В.А. Оганесян
и др. - М. Просвещение, 1975.
8. О совершенствовании методов обучения математике. Пособие для учителей / В.С.
Крамор - М.: Просвещение, 1988
31
Приложение 1.
Умножение и деление степеней
Умножение
При умножении степеней с одинаковым основанием основание оставляют прежним, а показатели степеней складывают.
an am = an + m
Задание
Запишите произведение в ви де степени:
а) 3 2 3 5;
б) x 3 x 4 x
Решение
а) 3 2 3 5 = 3 2 + 3 = 3 7;
б) x 3 x 4 x = x
3+4+1
=x8.
Деление
При делении степеней с одинаковыми основаниями основа ние оставляют прежним, а из показателя степени делимого вы читают показатель степени делителя.
am : an = a m - n
Задание
Решение
Выполните деление:
а) 7 12 : 7 10 ;
а) 7 12 : 7 10 = 7 12 - 10 =7 2 ;
15
8
б) x : x .
б) x 15 : x 8 = x 15 - 8 = x 7
Возведение в степень произведения и степени
При возведении в степень произведения возводят в эту степень каждый множитель и результаты перемножают.
(a b) n = a n b n
Задание
Возведите в степень:
а) (m n) 2 ;
б) (- а) 3 ;
в) (10cd) 4 .
Решение
а) (m n) 2 = m 2 n 2 ;
б) (- а) 3 = (-1) 3 а 3 ;
в) (10cd) 4 = 104 с4 d 4
При возведении степени в степень основание оставляют тем
же, а показатели перемножают.
( am) n= a m
n
Задание
Возведите в степень:
г) (x 3 ) 4;
д) (2n 2 ) 3 ;
Решение
г) (x 3 ) 4 = x 3 4 = x 12 ;
д) (2n 2 ) 3 = 2 3 (n 2 ) 3 = 8n 6;
Упростите:
е) y 3 (y 2 ) 4;
е) y 3 (y 2 ) 4= y 3 y 2 4= y 3 y 8=
= y 3 + 8 = y 11
32
Приложение 2.
Тест на закрепление нового материала.
1. Степенью числа а с натуральным показателем n, большим 1, называется произведение------------------------------------------------множителей, каждый из которых равен ----------------------- : аn=------------------ .
2. 43 =---------------------------=---------, здесь 4- ----------------степени, 3- ----------степени, 64- ---------------степени 43.
3. Вычисление значения степени называют действием-----------------------------.
4. при умножении степеней с одинаковыми основаниями основание остается прежним, а
показатели степеней---------------------------- .
5. аm: an=-----------,(m>n, a o).
6. При возведении степени в степень основание остается прежним, а показатели степеней----------------- .
7. (ab)n= ---------------------- .
8. При возведении дроби в степень следует в эту степень -------------------------.
Итоговый тест по теме « Свойства степени с натуральным показателем»
1. Выполни деление степеней 215  23
1)
212
2)
25
3)
245
2. Запиши в виде степени (х-у)(х-у)=…
1)
х2-у2
2)
(х-у)2
3)
2(х-у)
3. Замени  степенью, чтобы выполнялось равенство а2 ·  =а10
1)
a5
2)
a8
3)
a-12
4. Чему равно значение выражения (2ас)4?
1)
8ас
2)
16ас4
3)
16а4с4
5. Из предложенных вариантов выбери тот, которым можно заменить * в
равенстве (*)2 = 310
1)
38
2)
35
3)
3-12
6. Укажи равенства, в которых допущены ошибки
1)
23 · 27 = 221
2)
(4х)3= 64х3
33
3)
230  210 = 220
4)
5·5·5·5=45
5)
(а2)3· (а4)2 = а5 · а6 = а11
7. Отметь номера верно выполненных сравнений степеней:
1)
(-7,6)5 < 0;
4) (-5,3)10 < 5,38;
2)
(-4,9)7 < (-4,9)4;
5) 0 < (-3,7)6.
12
12
3)
(-9) = -9 ;
8. Какое слово надо вписать вместо многоточия?
Степенью числа а с натуральным показателем n, большим 1, называется … n
множителей, каждый из которых равен а.
9. Упрости выражение (а3)5  (a3 · а2) по действиям. Укажи номера верных ответов
действий.
1)
а3
2)
a5
3)
a6
4)
a10
5)
а15
36  27
10. Найди значение дроби
812
Тест по теме « Свойства степени с натуральным показателем»
Представить в виде степени.
I.
II.
III.
IV.
V. Поставьте вместо звездочки нужное выражение.
VI. Сравните с нулем выражения.
34
Приложение 3.
Тест по теме: Степень с натуральным показателем. Одночлен.
I вариант.
1. Записать произведение в виде степени 2а2а2а2а2а:
Варианты ответов: а) 2а5;
б) 32а5;
в) (2а)5;
г) а5.
2
2
2. Вычислить: -9   + 52.
3
Варианты ответов: а) -1; б) 21; в) 19; г) 11.
3. Найти n, k, m, если известно, что аn a = a17; bk:b2 = b4 ; (c3)m = c15.
Варианты ответов: а) n = 17; k = 6; m = 5; б) n = 16; k = 6; m = 5; в) n = 16; k = 6; m
= 12; г) n = 16; k =8; m = 5.
3   3
3 
2 5
4. Используя свойства степеней, вычислить
7
5 3
Варианты ответов: а) 9;
б) 27;
в) 81;
г) 14.
5
m m
Упростите выражение
.
m7
Варианты ответов: а) m16;
б) m9;
в) m13;
г) m2.
Из данных выражений назвать те, которые являются одночленами:
6х
1
1) х – у;
2) 5,2х2у;
3) в2 + 2в;
4) 4m2n;
5)
;
6)
.
t
ав
Варианты ответов : а) 1 и 3;
б) 2 и 4;
в) 5 и 6;
г) 2.
3
5 2
Записать одночлен в стандартном виде 2х (-2х ) .
Варианты ответов: а) 8х13;
б) 4х10;
в) –8х28;
г) –4х21.
1
Представить выражение в виде квадрата х 6 у 4
9
4
5.
6.
7.
8.
2
1

Варианты ответов: а)  х 3 у 2  ;
3

3
12
9. Вычислить 3 2 .
23
Варианты ответов : а) 8;
2
1

б)  х 4 у 2  ;
9

б) 16;
в)
1
;
4
2
1

в)  х 4 у 2  ;
3

2
1

г)  х 3 у 2  ;
9

г) 24.
10. Найти значение выражения А, если –3х4у5 = А9х2у3, при х = -2, у =
2
;
3
16
16
8
8
;
б) ;
в) ;
г) - .
27
27
3
3
8 3 3 n-1
9 2 5 n+1
11. Известно, что для а  0 , в  0 и с  0 числа (-2) а в с и (-3) а в с имеют
одинаковые знаки. Определите знак числа а.
Варианты ответов: а) а > 0;
б) a < 0.
Варианты ответов: а)
Тест по теме: Степень с натуральным показателем. Одночлен.
II вариант.
1. Записать произведение в виде степени 3х3х3х3х:
Варианты ответов: а) (3х)4;
б) 81х4;
в) 3х4;
г) х4.
35
2
3
2. Вычислить: -25   + 23.
5
Варианты ответов: а) -1; б) -7; в) -9; г) -37.
3. Найти n, k, m, если известно, что аn a = a12; b8:bk = b3 ; (cm)5 = c15.
Варианты ответов: а) n = 12; k = 5; m = 3; б) n = 11; k = 5; m = 3; в) n = 12; k = 11;
m = 10; г) n = 11; k = 24; m = 10.
2   2
2 
5 2
4. Используя свойства степеней, вычислить
Варианты ответов: а) 32;
5.
6.
7.
8.
б) 13
1
;
3
4 3
в) 8;
8
.
г) 64.
m3  m8
Упростите выражение
.
m9
Варианты ответов: а) m20;
б) m15;
в) m2;
г) m5.
Из данных выражений назвать те, которые являются одночленами:
х
z
1)
;
2) 3,5ху2;
3) с2 + 5с;
4) 2х5с;
5) 2 ;
6) m + n.
5 х
2t
Варианты ответов : а) 1 и 5;
б) 2;
в) 2 и 3;
г) 2 и 4.
5
3 2
Записать одночлен в стандартном виде 5х (-3х ) .
Варианты ответов: а) 15х11;
б) -15х11;
в) –45х10;
г) 45х11.
1 6 8
а в
Представить выражение в виде квадрата
25
2
1

Варианты ответов: а)  а 3 в 4  ;
5

3
20
9. Вычислить 3 2 .
25
Варианты ответов : а) 4;
б)
б)


1 3 4
а в ;
25
1
;
5
в) 8;
2
1

в)  а 4 в 6  ;
5

2
 1

г)  а 4 в 6  ;
 25

г) 40.
10. Найти значение выражения В, если –45х3у5 = В5х4у3, при х = -3, у =
1
;
6
1
5
1
3
;
б)
;
в)
;
г) .
8
12
12
8
11. Известно, что для а  0 , в  0 и с  0 числа (-5)6а5в7n+1 и (-4)3а4в5сn-1 имеют
одинаковые знаки. Определите знак числа а.
Варианты ответов: а) а > 0;
б) a < 0.
Варианты ответов: а)
36
Приложение 4.
Опорный тест теоретического материала по теме:
«Сложение и вычитание многочленов»
1. Одночленом называется:
а) произведение чисел.
б) частное чисел и степеней.
в) произведение чисел, переменных и их степеней.
2. Коэффициентом одночлена называют:
а) числовой множитель одночлена.
б) показатель степени одночлена.
в) знак одночлена.
3. Подобными, называются одночлены:
а) у которых одинаковые коэффициенты.
б) у которых одинаковая буквенная часть.
в) имеющие одинаковые знаки.
4. Многочленом называется:
а) сумма или разность нескольких одночленов.
б) произведение нескольких одночленов.
в) частное нескольких одночленов.
5. При сложении многочленов:
а) скобки раскрываем с изменением знаков у одночленов в скобках на
противоположные и затем приводим подобные слагаемые.
б) скобки раскрывать не нужно.
в) скобки раскрываем без изменения знаков у одночленов в скобках и затем
приводим подобные слагаемые.
6. При вычитании многочленов:
а) нужно поменять знаки у одночленов в скобках, перед которыми стоит знак
минус и затем привести подобные слагаемые.
б) скобки раскрывать не нужно.
в) скобки раскрываем без изменения знаков у одночленов в скобках и затем
приводим подобные слагаемые.
Разноуровневая самостоятельная работа по теме «Сложение и вычитание многочленов»
Вариант – 1
1. Найдите сумму многочленов:
(5 + 4a) + (9 – 7a) = ?
2. Найдите разность многочленов:
(12b2 – 8) – (4 + 8b2) = ?
Вариант – 2
1. Найдите сумму многочленов:
(12 + 4х) + (3 – 8х) = ?
2. Найдите разность многочленов:
(17у2 – 9) – (7 + 12у2) = ?
37
Вариант – 3
1. Найдите сумму многочленов:
(6 + 5a) + (8 – 8a) = ?
2. Найдите разность многочленов:
(14b2 – 10) – (2 + 10b2) = ?
Вариант – 4
1. Найдите сумму многочленов:
(9 + 6х) + (6 – 10х) = ?
2. Найдите разность многочленов:
(18у2 – 11) – (5 + 13у2) = ?
----------------------------------------------------------------------------------------------------Вариант – 5
1. Найдите сумму многочленов:
(11 + 6a) + (3 – 9a) = ?
2. Найдите разность многочленов:
(16b2 – 9) – (3 + 12b2) = ?
Вариант – 6
1. Найдите сумму многочленов:
(4 + 9х) + (11 – 13х) = ?
2. Найдите разность многочленов:
(20у2 – 2) – (14 + 15у2) = ?
Вариант – 7
1. Найдите сумму многочленов:
(a2 – a +9) + (2a2 – 17 + a) = ?
2. Найдите разность многочленов:
(12у3 – 8y2) – (12y2 + 17у3 + 5) = ?
Вариант – 8
1. Найдите сумму многочленов:
(х3 – 2х +8) + (3х3 – 19 + 2х) = ?
2. Найдите разность многочленов:
(24b3 – 5b2 + 13) – (12b2 + 17b3 + 5) = ?
----------------------------------------------------------------------------------------------------Вариант – 9
1. Найдите сумму многочленов:
(–2а2 – 2a + 11) + (5a2 – 19 + 2a) = ?
2. Найдите разность многочленов:
(14у3 – 7y2 – 8) – (13y2 + 19у3 – 3) = ?
Вариант – 10
1. Найдите сумму многочленов:
(7х3 – 5х + 5) + (–3х3 – 16 + 5х) = ?
2. Найдите разность многочленов:
(12b3 – 9b2 + 24) – (8b2 + 5b3 + 16) = ?
Вариант – 11
1. Найдите сумму многочленов:
38
(–4а2 – 4a + 15) + (7a2 – 23 + 4a) = ?
2. Найдите разность многочленов:
(17у3 – 5y2 – 9) – (15y2 + 22у3 – 4) = ?
Вариант – 12
1. Найдите сумму многочленов:
(9х3 – 7х + 11) + (–5х3 – 22 + 7х) = ?
2. Найдите разность многочленов:
(14b3 – 13b2 + 24) – (4b2 + 7b3 + 16) = ?
Самостоятельная работа .
Найти сумму или разность многочленов А и В для указанных клеток таблицы и выбрать
букву соответствующую полученному результату.
А\В
х+4
5а-4
2х-1
3-2а
5х-3а
х2+а
а2-х2
2х+1
1
2
3
4
5
6
7
2а-3
8
9
10
11
12
13
14
-3х-2
15
16
17
18
19
20
21
4х+3а
22
23
24
25
26
27
28
а2-ах
29
30
31
32
33
34
35
х2+4а
36
37
38
39
40
41
42
а2+х2
43
44
45
46
47
48
49
Вариант 1
Вариант 2
Вариант 3
1) Найди сумму или
разность многочленов А и
В, для клеток:
1) Найди сумму или
разность многочленов А и
В, для клеток:
1) Найди сумму или
разность многочленов А и
В, для клеток:
41(А+В), 34(А+В), 9(А-В),
15(А+В), 15(А-В), 19(А+В),
12(А+В), 35(А-В), 21(А-В),
40(А-В).
29(А+В), 12(А-В), 48(А+В),
3(А-В), 49(А+В), 11(А+В),
19(А-В), 40(А+В), 34(А-В),
49(А-В).
11(А-В), 17(А+В), 9(А+В),
35(А+В), 41(А-В), 26(А+В),
26(А-В), 17(А-В), 29(А-В),
3(А+В).
Строго по порядку!
Строго по порядку!
Строго по порядку!
2) Среди ответов выбрать
нужный и выписать букву.
2) Среди ответов выбрать
нужный и выписать букву.
2) Среди ответов выбрать
нужный и выписать букву.
Ответы:
Ответы:
Ответы:


5х-а-3 И
5а-5х-3 С


5х-а-3 Р
5а-5х-3 С
39


5х-а-3 Ч
5а-5х-3 Ю






























-3х+а2-х-2 Х
-3х-а2+х2-2 А
2а2-ах-х2 Ц
х2-ах Б
х2+5х+а Й
х2+7а-5х Т
2х2+5а У
3а В
2х2+а2+а Я
а2-а К
2а2 Ф
2х2 П
9х Ч
-х+6а Ж
-х-3 Д
-5х-1 Щ
-2х+2 Л
-4х-6 О
0Ё
4а-6 Г
а2+х2-ах+а М
а2-х2-ах-а Р
2х-3а-2 Ш
-8х+3а-2 З
7а-7 Н
-3а+1 Е
4х Ъ
2а2-ах+х+4 Ь
а2-ах-х-4 Ю






























-3х+а2-х-2 Х
-3х-а2+х2-2 А
2а2-ах-х2 Ц
х2-ах Б
х2+5х+а Й
х2+7а-5х Т
2х2+5а Ф
3а В
2х2+а2+а Я
а2-а К
2а2 У
2х2 П
9х Ч
-х+6а Ж
-х-3 Д
-5х-1 Щ
-2х+2 Л
-4х-6 О
0М
4а-6 Г
а2+х2-ах+а Ё
а2-х2-ах-а И
2х-3а-2 Ш
-8х+3а-2 Е
7а-7 Н
-3а+1 З
4х Ъ
2а2-ах+х+4 Ь
а2-ах-х-4 Ю
Поговорка: “Умел ошибаться - умей и поправиться”.
40






























-3х+а2-х-2 Х
-3х-а2+х2-2 Ц
2а2-ах-х2 А
х2-ах Б
х2+5х+а Й
х2+7а-5х Ж
2х2+5а У
3а В
2х2+а2+а Ъ
а2-а К
2а2 Ф
2х2 Д
9х И
-х+6а Т
-х-3 П
-5х-1 Ь
-2х+2 Л
-4х-6 Г
0Ё
4а-6 О
а2+х2-ах+а М
а2-х2-ах-а Н
2х-3а-2 Ш
-8х+3а-2 З
7а-7 Р
-3а+1 Е
4х Я
2а2-ах+х+4 Щ
а2-ах-х-4 С
Приложение 5.
Тест. Умножение одночлена и многочлена
1. Выполните умножение -5х.(-3х+2х2-2)
-10х3-15х2+10х
-10х3+15х2-10х
-10х3-15х2+10
-10х3+15х2+10х
2. Какой многочлен надо поставить вместо звездочки (*), чтобы выполнялось
равенство:
-2х2.(*)=-8х4а2+4х2а-6х4
4а2х-2а-3х2
3х2-2а+4а2х2
2а-3х2-4а2х2
-4а2х2+3х2+2а
3. Упростите выражение 3а(2в-а)-4в(в+2а)
3а2-4в2
-3а2-2ав-4в2
3а2+2ав+4в2
-3а2-4в2
4. Реши уравнение: 7х2+х=0
х=0
х= -(1/7)
х=0 и х= -7
х=0 и х= -(1/7)
Тест. Умножение многочлена на многочлен.
1. Выполните умножение (5в-4).(-2в-3)
-10в2+7в-12
-10в2-7в+12
10в2-15в+8в-12
10в2-7в-12
2. Представьте в виде многочлена (2х-2).(-х2+7х-1)
-2х3+16х2+16х-2
-2х3+16х2-16х+2
-2х3+1х2-12х+2
-2х3-12х2+12х-2
3. Представить в виде многочлена выражение
-3а2-14а-16
-3а2-10а-16
3а2+14а
-3а2-10а
4. Найди корень уравнения
8-(3а-2)(а-4)
15х2 - (3х-2)(5х+4)=-8. Ответ:
41