Задание 1 эпюр
реклама
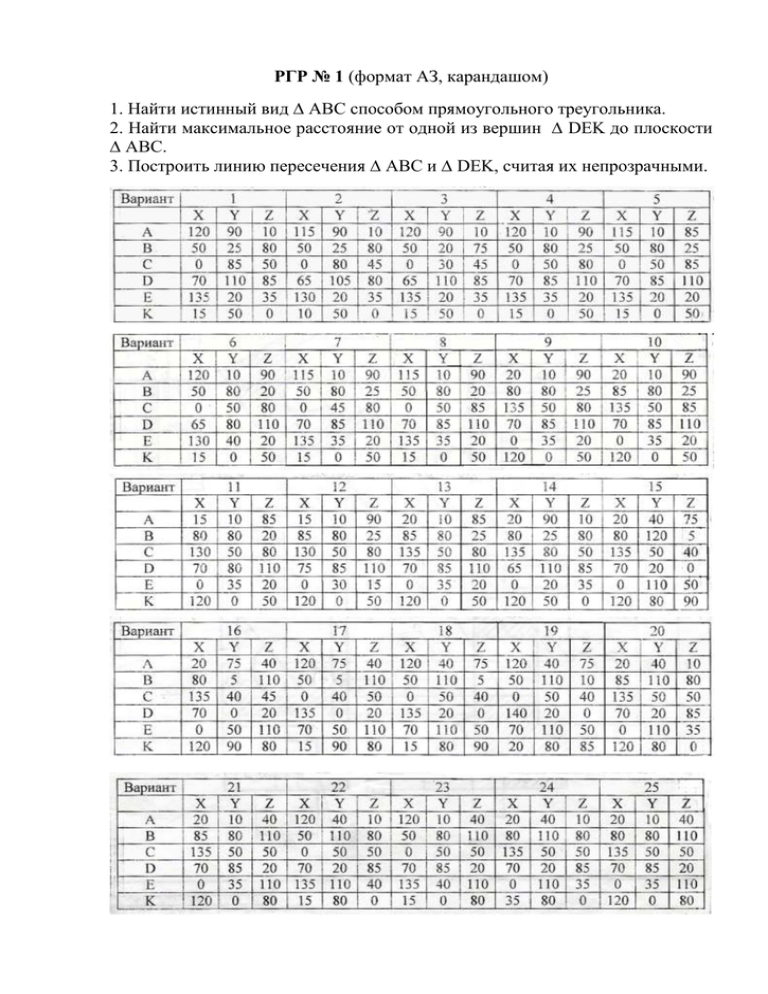
РГР № 1 (формат АЗ, карандашом)
1. Найти истинный вид ∆ АВС способом прямоугольного треугольника.
2. Найти максимальное расстояние от одной из вершин ∆ DEK до плоскости
∆ АВС.
3. Построить линию пересечения ∆ АВС и ∆ DEK, считая их непрозрачными.
Ï åðâ. ï ðèì åí .
í àò óðàëüí àÿ âåëè÷èí à î ò ðåçêà BÑ
í àò óðàëüí àÿ âåëè÷èí à î ò ðåçêà ÀÑ
2
B2
B2
32
Ã2
B2
R2
22
N2
T2
C2
A2
Ñï ðàâ. ¹
12
h2
C2
22
A2
x12
M2
42
K2
12
f2
C2
32
P2
A2
P2
x12
x12
í àò óðàëüí àÿ âåëè÷èí à î ò ðåçêà ÀB
B1
B1
P1
P1
B1
21
11
Ï î äï . è äàò à
K1
C1
Èí â. ¹ äóáë.
A1
h1
41
M1
11
N1
f1
A1
T1
C1
21
31
A1
C1
31
R1
í àò óðàëüí àÿ âåëè÷èí à
ðàññò î ÿí èÿ î ò Ð äî (ÀÂÑ)
A
Â
Èçì . Ëèñò ¹ äî êóì .
Ðàçðàá. Èâàí î â
Ï ðî â.
Ï åò ðî â
Ò.êî í ò ð.
Èí â. ¹ ï î äë.
Ï î äï . è äàò à
Âçàì . èí â. ¹
Ñ
Í .êî í ò ð.
Óò â.
Î áðàçåö âûï î ëí åí èÿ ýï þðà ¹ 1
Ï î äï . Äàò à
Ëèò .
Ì àññà Ì àñøò àá
Ýï þð ¹ 1
1:1
Ëèñò
Ëèñò î â
1
ÀÃÒÓ, ÄÌ Ì - 11
Êî ï èðî âàë
Ôî ðì àò
A3
Задачи к РГР №1
Точка на чертеже Монжа
5. Построить эпюры точек, лежащих во 2-ой, 3-ей, 4-ой четвертях и удаленных от горизонтальной
плоскости проекций на расстояние 30 мм, а от фронтальной - на расстояние 15 мм.
6. Дана точка А, лежащая в 1-ой четверти на расстоянии 30 мм от П1 и 15 мм от П2. Построить эпюры
точек, симметричных данной точке А относительно П1, П2 и оси ОХ.
7. Указать, где расположены точки, заданные своими эпюрами (Рис. 5).
Â2
À1
Â1
x12
À2
Å2
M1
Å1 D1=D2
M2 N1
Ñ2
F2
Ñ1
F1
N2
Рис. 5
8.
Дан куб своими проекциями и точка А внутри его (Рис. 6).
Построить точки, симметричные точке А:
а) относительно нижней грани;
б) относительно правой грани;
в) относительно передней грани;
г) относительно левого переднего ребра;
д) относительно левого нижнего ребра;
е) относительно правой верхней передней вершины
à),á)
À2
â),ã)
À1
À2
ä),å)
À2
À1
À1
Рис. 6
10. На трехкартинном комплексном чертеже построить проекции точек, заданных своими
координатами, и определить, в каком октанте они находятся.
A
B
C
D
E
X
10
-10
50
60
-10
Y
20
20
-40
50
-20
Z
30
30
-50
-40
-30
11. Построить проекции точек, симметричных точкам A, B, C (см. предыдущую задачу) относительно
плоскостей проекций П1, П2, П3, и указать, в каких октантах они окажутся. Записать их координаты.
12. Построить проекции точек В(0,20,30), С(10,0,30), D(10,20,0), Е(10,0,0), F(0,20,0).
13. Построить проекции плоскости ABC: А(120,90,10), В(50,25,80), С(0,85,50).
2.2 Прямая линия
14. Через точку А(60;40;20) провести горизонталь под углом 30 ˚ к П2 и фронталь под углом 45˚ к П1.
15. Построить проекции отрезка АВ на П1, П2, П3 по данным координатам А (20;10;40); В (60;40;10).
Построить проекции точки С Є{АВ}, если Хс = 30. Найти Yc и Zc.
16. Определить положение прямых (Рис. 8).
E2
H2 =G2
A2
B2
h2
f2
F2
x12
G1
E1=F1
H1
h1
A1
f1
B1
Рис. 8
17. Построить проекции прямой I, проходящей через точку А и параллельной прямой m (Рис. 9).
m2
A2
x12
m1
A1
Рис. 9
18. Постройте через точку А горизонталь и фронталь, пересекающие прямую MN (Рис. 10).
M2
A2
N2
x12
M1
A1
N1
Рис. 10
19. Провести прямую, проходящую через точку А (10;10;10), параллельно плоскости XОZ и
пересекающую прямую, проходящую через точки В (30;30;30) и С(20;-30;-10).
2.3 Плоскость
21. Построить проекции плоскости ABC: А(1;2;0); B(3;0;4); С(0;3;2).
22. Построить чертеж плоскости, зная, что эта плоскость проходит через точки А (2;3;5) и В (4;8;2), а
также:
a. проходит через точку С(1;2;5),
б проходит через начало координат,
в является горизонтально-проецирующей,
г является фронтально-проецирующей,
д является профильно-проецирующей.
23. Даны точки А(3;2;3), В(-1;4;-1) и С(2;-1;4).. Построить изображения:
а) горизонтально-проецирующей плоскости, проходящей через точки В и А,
б) фронтально-проецирующей плоскости, проходящей через точки В и С, в) профильно-проецирующей
плоскости, проходящей через точки А и С.
24. По двум разноименным проекциям точек А и В, принадлежащим плоскости общего положения,
заданной двумя параллельными прямыми
с (с1, с2) и d (d1, d2), построить проекции отрезка АВ (Рис. 12).
A2
ñ2
d2
x12
B1
d1
c1
Рис. 12
25. В плоскости, заданной двумя параллельными прямыми а и b, провести горизонталь на расстоянии 10
мм от П1 и фронталь на расстоянии 20 мм от П2.
2.4 Позиционные задачи
26. Построить точку пересечения прямой с плоскостью и определить видимость, если: прямая l
горизонтально-проецирующая, а плоскость ABC – общего положения (Рис. 13).
l2
Â2
À2
Ñ2
x12
À1
Â1
l1
Ñ1
Рис. 13
27. Построить линию пересечения плоскости ABC и фронтально-проецирующей плоскости G (Рис. 14).
B2
G2
A2
C2
A1
C1
B1
Рис. 14
31. Построить точку пересечения прямой общего положения с плоскостью общего положения (Рис.
18).
B2
l2
C2
x12 A2
l1
A1
C1
B1
Рис. 18
34. Построить линию пересечения АВС и плоскости, заданной параллельными прямыми ED и FG
(Рис. 21).
E2
A2
G2
D2
B2
F2
F1
C2
A1
G1
E1
D1
C1
Рис. 21
B1
2.5.2 Перпендикулярность прямых
39. Построить горизонтальную проекцию равнобедренного треугольника АВС (А1В1С1, А2В2С2),
основанием которого служил бы отрезок АВ (А1В1, А2В2), параллельный плоскости проекции П1 (Рис.
26), если дана его фронтальная проекция А2В2С2.
Ñ2
Â2
À2
õ12
Â1
À1
Рис. 26
40. Достроить проекции прямоугольного треугольника АВС по заданной гипотенузе АВ, если известно,
что вершина С его принадлежит прямой уровня h (Рис. 27).
À2
h2
B2
A1
B1
h1
Рис. 27
47. Через точку А провести перпендикуляр к плоскости, заданной прямыми АВ и АС и отложить на нем
отрезок, равный l (Рис. 33).
B2
l
A2
C2
B1
A1
C1
Рис. 33
49.
Построить
точку,
симметричную
плоскости треугольника АВС (Рис. 35).
данной
Â2
À2
Ì
Ñ2
2
À1
Ñ1
Ì
Â1
1
Рис. 35
точке
М
относительно
51. Найти расстояние от точки А до плоскости SCD пирамиды SBCD (Рис. 37).
S2
A2
Â2
Â1
D2
C2
C1
S1
A1
D1
Рис. 37
56. Построить проекции пирамиды, если известно ее основание АВС и высота h = 60 мм, опущенная в
центр тяжести этого треугольника
Вопросы к экзамену и зачету по курсу «Начертательная геометрия» и «Инженерная графика»
1. Введение. Предмет начертательной геометрии. Метод проецирования. Виды проецирования. Свойства
параллельных проекций. Комплексный чертеж. Преимущества и недостатки эпюра Монжа.
2. Точка, прямая, плоскость, многогранники на эпюре Монжа.
3. Позиционные задачи на прямые и плоскости.
4. Прямые общего и частного положения.
5. Плоскости частного положения.
6. Взаимное расположение прямой и плоскости.
7. Положение плоскости в пространстве
8. Прямые и плоскости проецирующие.
9. Прямые и плоскости уровня.
10. Пересечение прямой с плоскостью. Определение видимости.
11. Пересечение двух плоскостей.
12. Метрические свойства прямоугольных проекций.
13. Определение истинной величины отрезка.
14. Теорема о проекциях прямого угла.
15. Способы преобразования комплексного чертежа.
16. Способ замены плоскостей проекций. Основные задачи
17. Способ плоско-параллельного перемещения.
18. Способ вращения вокруг линии уровня.
19. Способ вращения вокруг проецируюшей прямой.
20. Многогранники. Пересечение многогранников плоскостью, прямой и между собой.
21. Кривые линии и поверхности. Определитель. Классификация поверхностей.
22. Поверхности вращения. Поверхности вращения второго порядка.
23. Линейчатые поверхности. Поверхности с плоскостью параллелизма.
24 Винтовые поверхности. Прямой геликоид. Наклонный геликоид.
25 Пересечение поверхностей (цилиндра, конуса, сферы, тора) плоскостью и с прямой линией. Взаимное
пересечение кривых поверхностей (способ вспомогательных плоскостей и сфер).
26.Развертки поверхностей многогранников и кривых поверхностей (точные и приближенные,
условные).
27 Построение развертки методом нормального сечения.
28.Аксонометрические проекции. Основные понятия и определения.
29.Основная теорема аксонометрии.
30.Прямоугольная аксонометрия и ее основные свойства.
31.Стандартные виды аксонометрических проекций.




