А.П.Ерохина. Методические указания по лаб.работам. (2 Мб, doc)

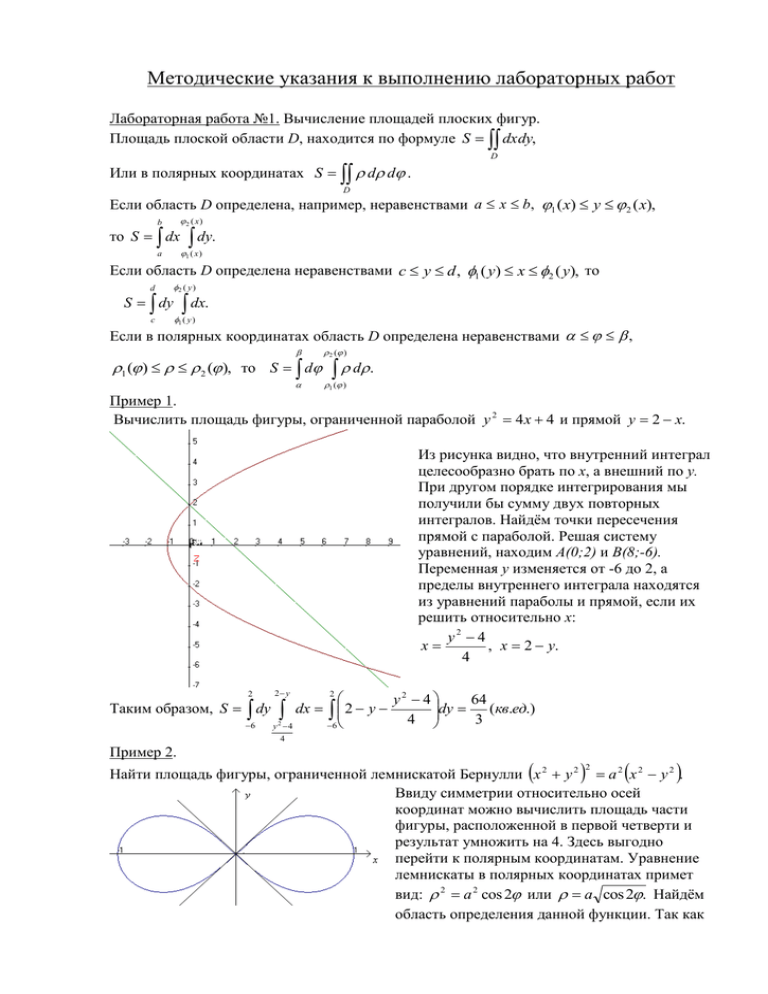
Методические указания к выполнению лабораторных работ
Лабораторная работа №1. Вычисление площадей плоских фигур.
Площадь плоской области D, находится по формуле S   dxdy,
D
Или в полярных координатах S    d d .
D
Если область D определена, например, неравенствами a  x  b, 1 ( x)  y   2 ( x),
b
2 ( x )
a
1 ( x )
то S   dx
 dy.
Если область D определена неравенствами c  y  d , 1 ( y)  x  2 ( y), то
d
2 ( y )
c
1 ( y )
S   dy
 dx.
Если в полярных координатах область D определена неравенствами      ,

1 ( )     2 ( ), то S   d

 2 ( )
 d .

 
1(
)
Пример 1.
Вычислить площадь фигуры, ограниченной параболой y 2  4 x  4 и прямой y  2  x.
Из рисунка видно, что внутренний интеграл
целесообразно брать по x, а внешний по y.
При другом порядке интегрирования мы
получили бы сумму двух повторных
интегралов. Найдём точки пересечения
прямой с параболой. Решая систему
уравнений, находим A(0;2) и B(8;-6).
Переменная y изменяется от -6 до 2, а
пределы внутреннего интеграла находятся
из уравнений параболы и прямой, если их
решить относительно x:
y2  4
x
, x  2  y.
4
2 y

y2  4 
64

dy 
Таким образом, S   dy  dx    2  y 
(кв.ед.)
4 
3
6
 6
y 2 4
2
2
4
Пример 2.


2


Найти площадь фигуры, ограниченной лемнискатой Бернулли x 2  y 2  a 2 x 2  y 2 .
Ввиду симметрии относительно осей
координат можно вычислить площадь части
фигуры, расположенной в первой четверти и
результат умножить на 4. Здесь выгодно
перейти к полярным координатам. Уравнение
лемнискаты в полярных координатах примет
вид:  2  a 2 cos 2 или   a cos 2. Найдём
область определения данной функции. Так как
cos 2  0, то 

2
 2n  2 
При n  0 получим 
при n  1 получим

4
Получаем S  4  d
0

4
 


4
2
 2n и 

4
 n   

4
 n .
, т.е. правая петля лемнискаты,
3
5
 
, (левая петля).
4
4

  d  2 
a cos 2
0
4


2 a cos 2
0
0
d  2a  cos 2 d  2a sin2 2
4
2
4
 a2.
2
0
0
Лабораторная работа №2. Вычисление объёмов тел.
Объём цилиндрического тела, ограниченного сверху поверхностью z  f ( x, y ) ,
снизу плоскостью z  0 и сбоку цилиндрической поверхностью вырезающей на плоскости
xOy область D, вычисляется по формуле V   f ( x, y)dxdy.
D
Объём области V можно находить и с помощью тройного интеграла
V   dv или V   dxdydz в декартовых координатах,
V
V
V    d d dz в цилиндрических координатах,
V
V   r 2 sin  d d dr в сферических координатах.
V
Во избежание возможных ошибок при вычислении объёма тела полезно сделать
пространственный рисунок, который давал бы представление о форме данного тела. Если
же тело построить не удаётся, то можно ограничиться хотя бы рисунком, изображающим
проекцию данного тела на одну из координатных плоскостей (область интегрирования
двойного интеграла). Однако и в этом случае необходимо представить себе, какая
поверхность ограничивает тело сверху.
Пример 3.
Вычислить объём тела, ограниченного поверхностями z  2  x  y, y  x 2 ,
y  x и z  0.
Сверху тело ограничено плоскостью z  2  x  y, снизу плоскостью xOy, с боков –
цилиндрической поверхностью y  x 2 и плоскостью y  x . Основанием тела, т. Е.
областью интегрирования является плоская область D, ограниченная параболой y  x 2 и
прямой y  x .

y 2  x
V   dx  (2  x  y )dy    2 y  xy 
dx 

 x2
2
2


0
x
0
1
x
1
1

x 2   2
x 4 
2
3

   2x  x 
 2x  x 
dx 

2  
2 

0
1
 x4

7x2
7
 
 x3 
 2 x dx  .
 2

2
20

0
Пример 4. Вычислить объём тела, вырезанного цилиндром x 2  y 2  4 x из шара
x 2  y 2  z 2  16 .
Заметим, так как оба уравнения поверхностей содержат сумму квадратов x 2  y 2 , то
удобнее перейти к цилиндрическим координатам x 2  y 2  4 x    4 cos  и
Уравнение сферы x 2  y 2  z 2  16   2  z 2  16 или z   16  z 2 .
В силу симметрии тела можно ограничиться
вычислением четвёртой части тела,
расположенной в первом октанте. Область
интегрирования – полукруг в первой

2
4 cos 
0
0
четверти. V  4  d

3
42
   (16   2 ) 2
30

16   2  d 
4 cos 
d 
0
128
2
(  )
3
3
Пример 5. Вычислить объём тела, ограниченного поверхностями hz  x 2  y 2 и z  h .
Решение. Снизу тело ограничено
x2  y2
параболоидом z 
, сверху
h
плоскостью z  h и проектируется в круг
x 2  y 2  h 2 плоскости xOy . Используем
цилиндрические координаты, в которых
2
уравнение параболоида примет вид z 
.
h
Объём тела равен V    d d dz 
V

2
h
h
2
0
0
2
0
 d   d  dz  
h
2
2
3  2
3

 h 2  4 
 3

  d  
 d   h  h  d  h .
d   h 

  2 4h 

 2
h 
4  0
2
0

0
0 
h
h
Лабораторная работа №3. Вычисление площади поверхности.
Если поверхность  задана уравнением z  z ( x, y ) и её проекция на плоскость xOy есть
область D, то площадь поверхности вычисляется по формуле S   ds или .

S

DxOy
2
2
 z   z 
1       dxdy .
 x   y 
Аналогично, если поверхность задана уравнением x  x( y, z ) , то
2

S
D yOz
2
 x 
 x 
1       dydz , где D yOz проекция поверхности  на плоскость yOz .
 z 
 y 
Если уравнение поверхности имеет вид y  y ( x, z ), то S 
2

DxOz
2
 y 
 y 
1       dxdz ,
 x 
 z 
где DxOz проекция поверхности  на плоскость xOz .
Пример 6. Найти площадь части конуса z  x 2  y 2 , заключённой внутри цилиндра
z
x
;

x 2  y 2  2 x. Находим частные производные из уравнения конуса:
2
2
x
x y
z

y
y
x2  y2
.
Областью интегрирования D является круг, ограниченный окружностью x 2  y 2  2 x
или ( x  1) 2  y 2  1 , то есть центр окружности в точке (1;0) и радиус равен 1.
Двойной интеграл удобнее считать в полярных координатах. Окружность x 2  y 2  2 x
в полярных координатах имеет вид   2 cos  . Тогда
S   1 
x2

y2
dxdy = 2  dxdy  S ( D)  2 (Площадь круга равна R 2 .
x y
x y
D
У нас R  1 ).
Лабораторная работа № 4. Вычисление длины кривой
2
2
2
2
D
 x  x(t )
Если плоская кривая AB задана параметрическими уравнениями 
. t  [ ;  ] , где
 y  y (t )
x(t ) и y (t ) дифференцируемые функции, причём точке A соответствует t   , точке B
значение t   , то длина кривой находится по формуле l 


( x ) 2  ( y ) 2 dt.

 x  x(t )

Для пространственной кривой , заданной уравнениями  y  y (t ) ,
 z  z (t )


аналогичная формула l 

t  [ ;  ] справедлива
( x ) 2  ( y ) 2  ( z ) 2 dt.

b
Если кривая AB задана уравнениям y  f ( x) , x  [a; b] , то l   1  ( f ( x)) 2 dx .
a
В случае задания плоской кривой в полярной системе координат    ( ) , 1     2 ,
то её длина находится по формуле l 
2

 2 ( )  (  ( )) 2 d
1
Пример 7. Найти длину кривой x 2  y 2  2 x .
В данном случае целесообразно перейти к заданию кривой в полярных координатах.
Уравнение окружности имеет вид   2 cos  .

l
2




4 cos 2   4 sin 2  d  2

2


2
d  2

2
2


 2 .
2
Замечание Уравнение x  y  2 x или ( x  1) 2  y 2  1 задаёт окружность с центром в
точке (1;0) и радиусом R=1. Известно, что длина окружности равна 2R .
2
2
Лабораторная работа № 4. Разложение функции в ряды Тейлора и Лорана.
Всякая бесконечно дифференцируемая дробь в интервале x  x0  r может быть
единственным образом разложена в сходящийся ряд Тейлора из этого интервала ряд
Тейлора с
f ( x0 )
f ( x0 )
f ( n ) ( x0 )
f ( x)  f ( x0 ) 
( x  x0 ) 
( x  x0 ) 2     
( x  x0 ) n     , если в этом
1!
2!
n!
( n 1)
f
(c)
интервале выполняется условие lim Rn ( x)  lim
( x  x0 ) n1  0 , где Rn (x) n


n
(n  1)!
остаток ряда, c  x0   ( x  x0 ) , 0    1.
На практике можно пользоваться следующей теоремой, которая даёт простое достаточное
условие разложимости f (x) в ряд Тейлора.
Теорема. Если модули всех производных функции f (x) ограничены в интервале
x  x0  r одним и тем же числом M  0 , то для любого x из этого интервала ряд Тейлора
функции f (x) сходится к f (x) .
f (0)
f (0) 2
f ( n ) (0) n
x
x   
x    ,
1!
2!
n!
называемый рядом Маклорена. Приведём примеры разложения в ряд Маклорена
некоторых элементарных функций.
При x  0 получается ряд f ( x)  f (0) 
x x2
xn

  
    x  (;)
1! 2!
n!
x3 x5
x 2 n1
n
sin x  x 

     (1)
    x  (;)
3! 5!
(2n  1)!
x2 x4
x 2n
cos x  1 

     (1) n
    x  (;)
2! 4!
(2n)!

 (  1) 2
 (  1)    (  n  1) n
(1  x)   1  x 
x   
x     , где
1!
2!
n!
 [1;1], если   0,

x  (1;1], если  1    0,
 (1;1), если   1

ex  1
1
 1  x  x 2  x 3      x n    , x  (1;1)
1 x
n 1
x2 x3
n x
ln( 1  x)  x 

     (1)
   , x  (1;1]
2
3
n 1
x3 x5
x 2 n 1
arctg x  x 

     (1) n
   , x  [1;1]
3
5
2n  1
1 x 3 1 3 x 5 1 3  5 x 7
1  3  5    (2n  1) x 2n1
arcsin x  x   
 

  

   , x  [1;1]
2 3 24 5 246 7
2  4  6    (2n) 2n  1
Для разложения f (x) в ряд Тейлора (Маклорена) нужно:
1) найти производные f ( x), f ( x),..., f ( n ) ( x),
2) сосчитать значения производных в точке x  x0 (для ряда Маклорена в точке
x  0 ),
3) написать ряд для заданной функции и найти его интервал сходимости,
4) найти интервал, в котором Rn ( x)  0 при n   . Если такой интервал
существует, то в нём сумма составленного ряда совпадает с функцией f (x) .
5)
Лабораторная работа № 5. Вычисление значений функций с помощью степенных рядов.
Для вычисления значения функции f (x) при x  x1 с заданной точностью
функцию в интервале ( R; R ) разлагают в степенной ряд
f ( x)  a0  a1 x  a 2 x 2      a n x n    , x1  ( R; R) . Точное значение f ( x1 ) равно сумме
этого ряда при x  x1 , а приближённое – частичной сумме S n ( x1 ) , т.е. f ( x1 )  S n ( x1 ) .
Точность этого равенства увеличивается с ростом n, а абсолютная погрешность равна
f ( x1 )  S n ( x1 )  rn ( x1 ) , где rn  a n 1 x1n 1  a n  2 x1n  2    
Таким образом, для оценки погрешности нужно оценить сумму отброшенных членов.
Если данный ряд знакопостоянный, то составляют ряд из модулей членов ряда и для него
стараются подобрать положительный ряд с большими членами, который легко бы
суммировался. Обычно это бесконечно убывающая прогрессия. В качестве оценки rn ( x1 )
берут величину остатка этого нового ряда. В случае знакопеременного ряда, члены
которого удовлетворяют признаку Лейбница, используется оценка rn ( x1 )  a n 1 x1n 1 .
Оценку остатка ряда можно производить с помощью остаточного члена ряда Маклорена
f ( n1) (c)
, где 0  c  x1
f ( x1 )  S n ( x1 )  rn ( x1 ) 
(n  1)!
Пример 8. Вычислить число e с точностью до 0,001.
1 1
1
x x2
xn
  
    подставим x  1: e  1           
В формулу e x  1  
1! 2!
n!
1! 2!
n!
Для нахождения числа e оставим n слагаемых и оценим ошибку rn (x) :
rn ( x) 

1
1
1
1 
1
1


  
1

    

(n  1)! (n  2)! (n  3)!
(n  1)!  n  2 (n  2)( n  3)


1 
1
1

    . В квадратных скобках стоит бесконечно убывающая
1 
2
(n  1)!  n  1 (n  1)

1
1
прогрессия с знаменателем q 
, тогда сумма прогрессии равна
.
1
n 1
1
n 1
1
1
1
1
n 1
1




Окончательно получаем
, т.е. rn ( x) 
.
1
n!n
(n  1)!
(n  1)! n
n!n
1
n 1

Подберём наименьшее натуральное число n, чтобы выполнялось неравенство
Подбором убеждаемся, что это неравенство выполняется при n  6 , поэтому
1 1 1 1 1 1
e  1        2,718
1! 2! 3! 4! 5! 6!
1
 0,001 .
n!n
Лабораторная работа № 5. Применение степенных рядов к вычислению определённых
интегралов.
Для приближённых вычислений неопределённых и определённых интегралов, в
случае, когда первообразная не выражается через элементарные функции или её
нахождение сложно, применяются степенные ряды.
b
Пусть требуется вычислить
 f ( x) dx с заданной точностью. Подынтегральную
a
функцию f (x) раскладываем в ряд по степеням x в интервале ( R; R ) , который включает
в себя отрезок [a; b] . Для вычисления заданного интеграла можно воспользоваться
теоремой о почленном интегрировании степенного ряда. Ошибка вычислений
определяется так же, как и при вычислении функций.
1
4
Пример 9. Вычислить  e  x dx с точностью 0,001.
2
0
Решение. Разложим подынтегральную функцию в ряд Маклорена в интервале (;)
2
e x  1 
x2 x4 x6


 
1! 2! 3!
1
Интегрируя обе части равенства на отрезке [0; ] , лежащем внутри интервала сходимости
4
1
1
1
2
4
6
3
5
7
4
4
4
2




x
x
x
x
x
x
(;) , получим  e  x dx   1 


    dx   x 


    

1
!
2
!
3
!
1
!

3
2
!

5
3
!

7




0
0
0
1
1
1
1
1
1



    . Так как
 0,0052  0,001 , а
 0,001 , то
3
5
7
3
4 1!3  4
2!5  4
3!7  4
1!3  4
2!5  4 5
погрешность по модулю меньше первого отброшенного члена (ряд Маклорена
1
4
1
1

 0,245
4 1!3  4 3
0
Лабораторная работа № 6. Применение степенных рядов к решению дифференциальных
уравнений.
В случаях, когда интегрирование дифференциального уравнения в элементарных
функциях невозможно или способ его решения слишком сложен, решение такого
Лейбнецкого типа). Получим  e  x dx 
2

уравнения следует искать в виде ряда Тейлора y   c n ( x  x0 ) n .Коэффициенты ряда cn
n 0
находят подстановкой ряда в уравнение и приравниванием коэффициентов при
одинаковых степенях ( x  x0 ) в обеих частях полученного равенства. Если удаётся найти
все коэффициенты ряда, то полученный ряд служит решением во всей своей области
сходимости. Этим способом можно интегрировать линейные дифференциальные
уравнения с переменными коэффициентами.
Пример 10. Решить задачу Коши для уравнения y   xy   y  x cos x; y (0)  0, y (0)  1 .
Сначала разложим правую часть в степенной ряд по степеням x, т.к. у нас x0  0.
 x2 x4

x cos x  x  1 

    .
2! 4!


Будем искать решение уравнения в виде ряда y  c0  c1 x  c 2 x 2  c3 x 3  c 4 x 4     .
Тогда y   c1  2c 2 x  3c3 x 2  4c 4 x 3  5c5 x 4    
y   2c 2  6c3 x  12c 4 x 2  20c5 x 3  30c6 x 4    
Из начальных условий находим c0  0, c1  1 . Подставим полученные ряды в исходное
уравнение
(2c 2  6c3 x  12c 4 x 2  20c5 x 3  30c6 x 4    )  x (c1  2c 2 x  3c3 x 2  4c 4 x 3  5c5 x 4    ) +
 x2 x4 x6

+ (c0  c1 x  c 2 x 2  c3 x 3  c 4 x 4    )  x  1 


    .
2! 4! 6!


Приравниваем коэффициенты при одинаковых степенях x:
2c 2  0
x0
6c3  2  1
x1
x 2 12c 4  3c 2  0
x 3 20c5  4c3   1 2
…………………….
1
1
1
Решая эту систему, находим: c2  c4  c6      c2 n  0 , c3   , c5  , c7   ,  
3!
5!
7!
3
5
7
x
x
x
Получаем искомое решение в виде ряда y  x 


    или y  sin x .
3! 5! 7!