Ключи и критерии оценки

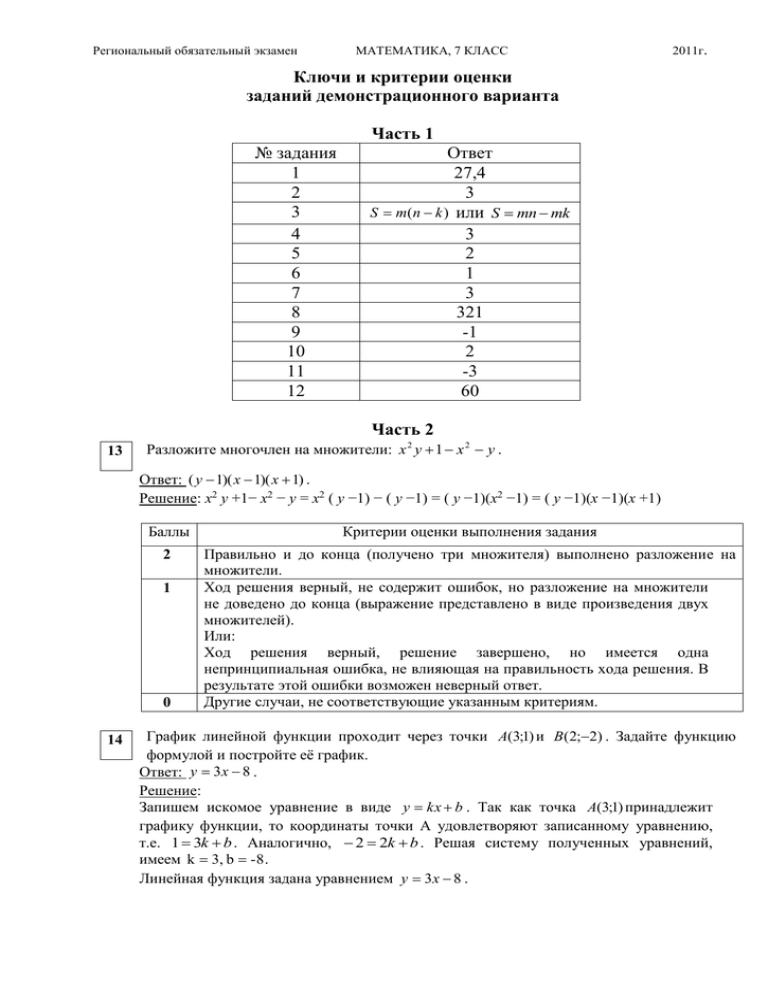
Региональный обязательный экзамен
МАТЕМАТИКА, 7 КЛАСС
2011г.
Ключи и критерии оценки
заданий демонстрационного варианта
Часть 1
№ задания
1
2
3
4
5
6
7
8
9
10
11
12
Ответ
27,4
3
S  m(n  k ) или S  mn  mk
3
2
1
3
321
-1
2
-3
60
Часть 2
13
Разложите многочлен на множители: x 2 y  1  x 2  y .
Ответ: ( y  1)( x  1)( x  1) .
Решение: x2 y +1− x2 − y = x2 ( y −1) − ( y −1) = ( y −1)(x2 −1) = ( y −1)(x −1)(x +1)
Баллы
Критерии оценки выполнения задания
2
Правильно и до конца (получено три множителя) выполнено разложение на
множители.
Ход решения верный, не содержит ошибок, но разложение на множители
не доведено до конца (выражение представлено в виде произведения двух
множителей).
Или:
Ход решения верный, решение завершено, но имеется одна
непринципиальная ошибка, не влияющая на правильность хода решения. В
результате этой ошибки возможен неверный ответ.
Другие случаи, не соответствующие указанным критериям.
1
0
14
График линейной функции проходит через точки A(3;1) и B (2;2) . Задайте функцию
формулой и постройте её график.
Ответ: y  3x  8 .
Решение:
Запишем искомое уравнение в виде y  kx  b . Так как точка A(3;1) принадлежит
графику функции, то координаты точки А удовлетворяют записанному уравнению,
т.е. 1  3k  b . Аналогично,  2  2k  b . Решая систему полученных уравнений,
имеем k  3, b  -8 .
Линейная функция задана уравнением y  3x  8 .
Региональный обязательный экзамен
2011г.
Баллы
Критерии оценки выполнения задания
3
Ход решения верный. Получена верная формула, задающая функцию. Верно
построен график функции.
Ход решения верный, решение завершено (получена формула, построен
график), но имеется одна непринципиальная ошибка, не влияющая на
правильность хода решения. В результате этой ошибки возможен неверный
ответ.
Или:
Ход решения правильный, в решении нет ошибок, но оно не является
полным (не построен график функции).
Другие случаи, не соответствующие указанным критериям.
2
0
15
МАТЕМАТИКА, 7 КЛАСС
Решите задачу.
В корзине у Нины было 16 грибов, а у Веры – 8 грибов. Они продолжали собирать
грибы еще некоторое время, причем Нина находила за 1 час 17 грибов, а Вера – 14
грибов. Через сколько часов у Нины грибов было в 1,5 раза больше, чем у Веры?
Ответ: через 1 час.
Решение:
Скорость, с которой Нина собирает грибы, составляет 17 грибов в час, скорость Веры
– 14 грибов в час.
Пусть t часов они продолжали собирать грибы. Тогда, за это время Нина набрала
17t грибов, а Вера - 14t грибов.
По условию задачи, через t часов в корзине у Нины было в 1,5 раза грибов больше,
чем у Веры, поэтому можно составить уравнение 17t  16  1,5(14t  8) . Решая
уравнение, получим t  1.
Баллы
Критерии оценки выполнения задания
3
Ход решения верный. Составлено и верно решено уравнение.
2
Ход решения верный, решение завершено, но имеется одна
непринципиальная ошибка, не влияющая на правильность хода решения. В
результате этой ошибки возможен неверный ответ.
Другие случаи, не соответствующие указанным критериям.
0