Ламинарное и турбулентное движение

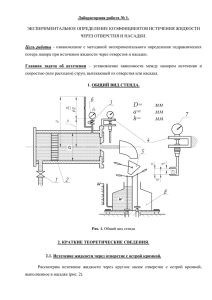
1
Методика по лабораторной работе №1
"Экспериментальное определение коэффициентов истечения"
1. Введение. Режимы движения жидкости: ламинарный и турбулентный.
Установка Рейнольдса для демонстрации режимов движения состоит из резервуара
с прозрачной трубкой и краном.
По оси стеклянной трубке вводится подкрашивающий раствор из дополнительной
емкости. Плотность раствора должна быть близкой к плотности воды, иначе струя,
которую он окрасит, будет проседать в трубке. Скорость регулируется вентилем в конце
трубки, подкрашенная краской струйка движется по оси трубки.
При небольшой скорости струйка подкрашенного раствора движется прямолинейно
по оси, как прямая натянутая струна, если в поток добавить еще окрашенные струйки, они
будут двигаться параллельными несмешивающимися линиями.
Ламинарным движением жидкости называется режим течения упорядоченным
слоями без перемешивания, то есть большая часть потока имеет скорости направленные
вдоль оси.
Струи жидкости, находящиеся на удалении от оси движутся с различными
скоростями. Наибольшую скорость имеет осевая струйка, на стенках трубы скорость
равна нулю.
При увеличении скорости нарушается устойчивость ламинарного течения,
появляются поперечные составляющие скорости. На устойчивость ламинарного режима
влияют вязкость жидкости, плотность, скорость движения частиц, размеры (диаметр)
трубопровода.
Разрыву струйки предшествует образование волнообразных колебаний. С усилением
колебаний струйка разрывается и затем полностью перемешивается с окружающей
жидкостью. Движение частиц производит впечатление беспорядочных вихрей.
Турбулентным движением жидкости называется режим течения
неупорядоченным слоями с перемешиванием.
Механизм турбулентного движения очень сложен. Частицы жидкости, в основном
двигаются вдоль трубопровода, но имеют и поперечные перемещения, перемешивающие
жидкость, происходит деформация жидкости.
Принято считать скорость движения у стенки равной нулю, затем скорость по
сечению возрастает.
Из величин μ, ρ, v, d влияющих на характер движения Рейнольдс выделил силы
инерции и вязкости, как оказывающие наибольшее влияние на режим движения и
составил их отношение, которое называется «числом Рейнольдса».
2
Re 
Fин Vd  Vd


Fвяз

v
При заданных: μ(ν) – вязкости, d - диаметре трубы, в эксперименте определяется
средняя скорость V потока жидкости в трубе.
При экспериментальных исследованиях Рейнольдс определил,
если
Re≤ 2300, режим движения – ламинарный,
если Re> 2300, режим движения - турбулентный.
Принято считать, что от 2300 до 4000 режим течения является переходным, при
некоторых условиях можно получить ламинарный режим до Re= 105. Однако, число Re =
2300 является критическим для перехода от ламинарного к турбулентному режиму.
2. Содержание лабораторной работы.
Целью лабораторной работы является изучение движения жидкости из отверстий и
насадков.
Задачи лабораторной работы: определение коэффициентов истечения.
Объектом лабораторной работы являются отверстия и насадки.
Рис.1. Отверстие (а) и насадки (б, в), используемые в лабораторной работе.
dс – диаметр струи в сжатом сечении, d – диаметр отверстия (рис.1а); для
цилиндрического насадка (рис.1б) диаметр насадка, для коноидального насадка (рис.1в) d
– выходной диаметр насадка.
3. Истечение через отверстие с острой кромкой.
При истечении через отверстие с острой кромкой вдали от отверстия жидкость
движется по резервуару, имея только осевые скорости. При приближении к отверстию на
расстояние l ≈0,5D, где D – диаметр цилиндра, движение становится криволинейным, так
3
как частицы жидкости устремляются к отверстию, радиальные составляющие скоростей
вызывают уменьшение осевых, как в резервуаре, так и за отверстием в струе. По мере
удаления от отверстия эти радиальные составляющие уменьшаются и далее в сечениях
струи на расстоянии (0,5-1)d, они практически отсутствуют.
Рис.2. Истечение через отверстие с острой кромкой. d – диаметр отверстия, dс диметр струи, dc<d, Vc – скорость движения жидкости в струе, Н – напор истечения, Ри –
давление, по которому определяется напор истечения, Ратм – атмосферное давление.
Ближайшее к отверстию сечение 2-2 , где скорости параллельны оси, расположено
на расстоянии l ≈ 0,5d. Это сечение круглой формы называется сжатым сечением струи,
так как его площадь fс меньше площади отверстия f.
3.1. Коэффициентом сжатия называется отношение площади сжатого сечения струи
к площади несжатого сечения или сечения отверстия, из которого вытекает струя.
 
fс
d
 ( c ) 2 . ε = fс/f
f
d
(1).
Диаметр сжатого сечения струи fс определяется экспериментально с помощью
микрометра.
2.Коэффициент скорости.
Уравнение Бернулли для сечений 1 и 2 имеет вид(рис.2) при истечении
реальной(вязкой) жидкости
P1
V12
P2
V2 2
V2 2
z1 

z 
 2

 g 1 2g 2  g
2g
2g
где Н  zi 
Pi
V2
 1 i это удельная энергия, проносимая потоком через i-e
g
2g
сечение, Н называется напором потока, это отношение энергии потока к весовому
расходу,
4
hп  
V2 2
- потери удельной энергии на трение от 1-го до 2-го сечения, zi– высота
2g
центра i-го сечения над плоскостью сравнения или геометрический напор, Рi– давление в
центре i-го сечения, Pi/ρg - пьезометрический напор, Vi – средняя скорость в i-м сечении,
V2/2g - скоростной напор, αi - коэффициент кинетической энергии, зависящий от
характера распределения скоростей по i-му сечению, ζi – коэффициент сопротивления
участка между первым и вторым сечением.
Для сечений 1-1 и 2-2: z1 = z2, P2 = Pат, и V1 <<V2 , поэтому скоростью V1
пренебрегаем.
Обозначив Ни 
P1  Pат Pи
- напор истечения, где Ри - давление, измеряемое

g
g
манометром. Обозначив V2 = Vc - скорость струи, получим
Pи
V2
V2
 2 с   с ,
g
2g
2g
Vc 
где  
1
2  
2g
Pи
  2 gH , (2)
g
1
Pи
- коэффициент скорости, Ни 
- напор истечения.
g
2  
Если бы трения в жидкости не было, уравнение Бернулли выглядело бы
Pи V 2
Н

, и скорость истечения была бы равна V  2 gН .
 g 2g
В нашем опыте V – это скорость жидкости в отверстии, когда она еще не сжата.
Коэффициентом скорости называется отношение скорости в сжатом сечении к
скорости в отверстии (или к скорости при истечении идеальной жидкости). Изменение
скорости в сжатом сечении струи в сравнении со скоростью жидкости в отверстии
оценивается коэффициентом скорости – φ.
3.3. Коэффициент расхода. Расходом жидкости называется объем жидкости,
проносимый через сечение потока в единицу времени, произведение скоростив сжатом
сечении на площадь этого сечения. Используя формулы, полученные выше
Q = fc*Vc = ε*f*φ* 2gH =μ*f*
где    * 
2 gH , (3).
QC
f *V
 C C – коэффициент расхода.
Qu f * 2gH
Коэффициентом расхода μ называется отношение расхода реальной жидкости к
расходу, определенному по скорости идеальной жидкости.
5
Коэффициенты ε , φ, μ называются коэффициентами истечения.
Величины коэффициентов истечения зависят от формы отверстия, от отношения
диаметра отверстия к напору истечения, от расстояния между отверстием и ближайшей к
нему стенкой резервуара, а также от режима движения жидкости, определяемом числом
Рейнольдса
Re 
Vd 


2 gHи
Vd

d,
v

где Ни – напор истечения, d – диаметр отверстия, ν – кинематическая вязкость
жидкости, μ – динамическая вязкость жидкости.
Зависимость коэффициентов истечения от числа Рейнольдса показана на рис.1. При
увеличении числа Re его влияние на коэффициенты истечения уменьшается.
Рис.3. Зависимость ε, φ,μ от числа Re для круглого отверстия с острой кромкой.
4. Истечение из насадков. Внешний цилиндрический насадок - трубка длиной l <
5d не изменяет форму струи до сжатого сечения (рис.4).
Безотрывной режим. После сжатого сечением струя может пройти насадок, касаясь
его внутренней поверхности - безотрывной режим истечения. При безотрывном режиме
струя на выходе будет иметь сечение равное сечению насадка fс = fн. Внутри насадка
имеется т.н. транзитная струя переменного сечения, область между насадком и струей
заполнена вращающейся жидкостью и нестабильна. При увеличении скорости транзитный
поток отрывается от насадка и устанавливается отрывной режим истечения.
Отрывной режим. При входе в насадок жидкость отрывается от стенок и движется,
как через отверстие с острой кромкой – отрывной режим истечения fс < fн.
6
Рис.4. Два режима истечения через цилиндрический насадок: а) безотрывной, б)
отрывной.
В коноидальном насадке (рис.1), образующие которого выполнены по форме струи,
поток заполняет насадок без отрыва. Площадь струи совпадает с площадью насадка fс =
fн.
4. Коэффициенты истечения μ, ε, φ определяются для круглого отверстия с острой
кромкой, внешнего цилиндрического насадка, коноидального насадка. Из соотношений
(1),(2),(3) следует
ε = (dс/d)2,
μ = Q /f*
2 gH , φ = μ/ ε,
где dс – диаметр струи.
5.Устройство опытной установки.
Рис.5. Устройство опытной установки. 1,3-вентили, 2 – успокоительные трубки, 4 –
устройство для измерения диаметра струи, 5 – клапан, 6 – манометр, 7 – индикаторная
головка, 8 – мерный бак. W – объем мерного бака, а – размах щечек, hи – размер,
определяемый по индикатору, h – высота установки манометра, Н – напор истечения., Ри значение давления по манометру.
7
5. Обработка результатов измерений.
5. 1.Расход установки
Q
W Wк  Wн

,
t
tк  tн
где Wк, Wн – соответствуют концу и началу измерения.
5.2. Диаметр струи
dc = а- hи, где а – размах щечек, hи – результат измерения по
индикаторной головке.
5.3.Напор истечения
Hи 
Pи
 h.
g
Ри – показания манометра, h – высота установки манометра над центром отверстия.
5.4 Коэффициент сжатия
5.5. Коэффициент расхода
ε = (dс/d)2 .

Q
, определяем расход установки, напор
f 2 gH
истечения, площадь струи – fс=ε*fo .
5.6. Коэффициент скорости φ = μ/ ε,
где dс – диаметр струи, d – диаметр отверстия.
5.7.Число Рейнольдса
Re 
Vd 


2 gH
Vd

d,
v

где ν – кинематическая вязкость воды, определяемая по графику, d – отверстия.
6. Выбираем ν , соответствующее 20ºС – 1*10-6м2/сек
Рис.6. Зависимость вязкости воды от температуры.
1. Сформулировать цель и задачи лабораторной работы.
2. Какие коэффициенты определялись в этой лабораторной работе?
3. В какой точке стенда определяется давление манометром?
4. Какая формула применяется для определения расхода? В каких единицах измеряется
расход?
8
5. Что такое: μ,φ,ε?
6. В каком месте измеряется скорость сжатой струи?
7. Что означает величина 2gH ?
8. Как записать число Рейнольдса, используя эту величину?
9. Какая связь между динамической и кинематической вязкостью? Записать число
Рейнольдса, используя кинематическую вязкость.
10. В каких единицах измеряется динамическая и кинематическая вязкость в СИ?
11. Какие области на графике μ,φ,ε = f(Re) можно выделить?
12. При одинаковом диаметре, что больше расход через отверстие с острой кромкой или
через коноидальный насадок?
13.Как называются режимы работы цилиндрического насадка?