Б2.Б.1 Математика

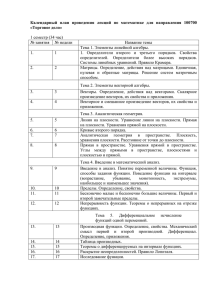
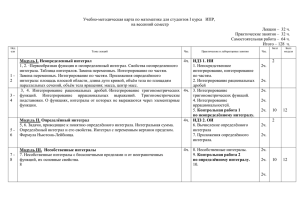
Аннотация к рабочей программе дисциплины
«Математика»
1. Цели освоения дисциплины.
Сформировать у студентов:
- способность использовать основные законы естественнонаучных дисциплин в
профессиональной деятельности, примененять методы математического анализа и моделирования
и экспериментального исследования;
- способность выявить естественнонаучную сущность проблем, возникающих в ходе
профессиональной деятельности, привлечь для их решения соответствующие физикоматематический аппарат;
- способность владеть основными методами, способами и средствами получения, хранения и
переработки информации, навыками работы с компьютером как средством управления
информацией.
2. Результаты обучения по дисциплине (приобретаемые компетенции).
- использование основных законов естественнонаучных дисциплин в профессиональной
деятельности, применение методов математического анализа и моделирования и
экспериментального исследования (ПК-1);
- способность выявить естественнонаучную сущность проблем, возникающих в ходе
профессиональной деятельности, привлечь для их решения соответствующие физикоматематический аппарат (ПК-2);
- владение основными методами, способами и средствами получения, хранения и
переработки информации, навыками работы с компьютером как средством управления
информацией (ПК-5).
В результате освоения дисциплины студенты должны:
знать фундаментальные основы высшей математики, включая алгебру, геометрию,
математический анализ, теорию вероятностей и основы математической статистики;
уметь самостоятельно использовать математический аппарат, содержащийся в литературе,
расширять свои математические познания;
владеть первичными навыками и основными методами решения математических задач из
общеинженерных и специальных дисциплин профилизации.
3. Трудоёмкость дисциплины составляет 12 ЗЕТ (432 часа)
4. Формы промежуточной аттестации – экзамен (1, 2, 3 семестры).
5. Содержание дисциплины.
Дисциплина «Математика» включает следующие разделы:
1. Линейная алгебра. Определители и их свойства. Вычисление определителей. Матрицы и
действия над ними.
2. Решение линейных систем. Метод Крамера. Метод Гаусса. Совместность систем.
3. Алгебра логики. Понятие высказывания. Логические операции над высказываниями.
4. Формулы алгебры логики. Равносильные формулы алгебры логики.
5. Векторная алгебра. Действия над векторами. Скалярное и векторное произведение, их
свойства.
6. Смешанное произведение и его свойства.
7. Прямая на плоскости. Общее уравнение прямой. Уравнение прямой с угловым
коэффициентом. Угол между прямыми. Условия параллельности и перпендикулярности прямых на
плоскости. Расстояние от точки до прямой.
8. Кривые второго порядка. Преобразование координат на плоскости. Полярные координаты.
9. Плоскость в пространстве, прямая в пространстве.
10. Прямая и плоскость в пространстве.
11. Некоторые элементы теории графов: виды графов, объединение и пересечение графов,
матрицы смежности и инцидентности.
12. Числовая последовательность и ее предел.
13. Предел функции.
14. Бесконечно малые и бесконечно большие функции.
15. Основные теоремы о пределах.
16. Первый и второй замечательные пределы.
17. Эквивалентные бесконечно малые функции. Применение эквивалентных бесконечно малых
функций.
18. Функции. Ограниченность, монотонность, периодичность, четность и нечетность функций.
Способы задания функции.
19. Непрерывность функции. Точки разрыва и их классификация.
20. Приращение аргумента и приращение функции. Определение непрерывности с помощью
этих понятий. Свойства непрерывных функций.
21. Определение производной, ее геометрический и механический смысл. Связь между
непрерывностью и дифференцируемостью функции.
22. Производная суммы, разности, произведения, частного.
23. Производные основных элементарных функций. Производная сложной функции.
24. Производная высших порядков. Дифференциал функции. Применение дифференциала к
приближенным вычислениям.
25. Правило Лопиталя. Возрастание, убывание функции. Экстремум функции.
26. Наименьшее и наибольшее значение функции на отрезке.
27. Выпуклость графика функции. точки перегиба. асимптоты графика функции.
28. Функция нескольких переменных и её область определения.
29. Частные производные первого порядка и их геометрическое истолкование. Частные
производные высших порядков.
30. Полный дифференциал функции. Применение полного дифференциала к приближенным
вычислениям.
31. Неопределенный интеграл и его свойства. Таблица основных неопределенных интегралов.
32. Основные методы интегрирования.
33. Понятие о рациональных функциях. Простейшие рациональные дроби и их интегрирование.
Интегрирование рациональных дробей.
34. Интегрирование тригонометрических функций.
35. Интегрирование иррациональных функций.
36. Интегрирования некоторых трансцендентных функций.
37. Интегральная сумма. Определенный интеграл и его свойства. Теорема о среднем значении.
38. Производная интеграла по переменной верхней границе. Формула Ньютона - Лейбница.
Замена переменной в определенном интеграле и интегрирование по частям.
39. Геометрические приложения определенного интеграла: площадь криволинейной трапеции,
длина дуги плоской кривой, дифференциал дуги, вычисление объема тел вращения, площадь
поверхности вращения.
40. Несобственные интегралы.
41. Дифференциальные уравнения I порядка: основные понятия, дифференциального уравнения
с разделяющимися переменными, однородные уравнения, линейные уравнения и уравнения
Бернулли.
42. Дифференциальные уравнения I порядка в полных дифференциалах интегрирующий
множитель.
43. Дифференциальные уравнения высших порядков, допускающие понижения порядка.
44. Линейные однородные дифференциальные уравнения 2-го и n-го порядков.
45. Линейные неоднородные дифференциальные уравнения. Системы дифференциальных
уравнений.
46. Числовые ряды, их свойства. Необходимое условие сходимости ряда.
47. Достаточные признаки сходимости ряда (сравнения, интегральный, Даламбера, Коши.
48. Знакочередующиеся, знакопеременные ряды.
49. Функциональные ряды. Степенные ряды.
50. Ряды Тейлора и Маклорена.
51. Разложение функций в ряды.
52. Приложения рядов к приближенным вычислениям.
53. Формулы комбинаторики. Предмет теории вероятностей. События, их виды. Полная группа
событий. Теоремы сложения и умножения вероятностей.
54. Вероятность появления хотя бы одного события. Формула полной вероятности. Формула
Бейеса.
55. Повторение испытаний. Биноминальный закон распределения. Локальная теорема Лапласа.
Интегральная теорема Лапласа. Теорема Пуассона.
56. Случайная величина. Дискретная случайная величина, закон ее распределения.
Математическое ожидание и его свойства. Дисперсия. Определение, свойства.
57. Непрерывные случайные величины. Функция распределения, плотность распределения,
математическое ожидание, дисперсия.
6. Место дисциплины в структуре основной образовательной программы.
Дисциплина «Математика» изучается в течение четырех семестров первого и второго года
обучения и потому может опираться на изученные в школе курсы математики.
Дисциплина «Математика» является дисциплиной естественнонаучного цикла, формирующая
у студентов творческий подход к деятельности инженера с нестандартным видением и оригинальным
подходом к современным процессам, обладающего гибким творческим научным мышлением,
способного чутко реагировать на изменения в развитии общества, научно-технического прогресса.
Поэтому, в первую очередь, в преподавании данной дисциплины следует обратить внимание на
привитие у студентов навыков нестандартного мышления при решении задач, позволяющих
достигать поставленных целей с наименьшими затратами всех видов ресурсов.
Данная дисциплина формирует у студентов творческий подход к деятельности инженера с
нестандартным видением и оригинальным подходом к современным процессам, обладающего
гибким творческим научным мышлением, способного чутко реагировать на изменения в развитии
общества, научно-технического прогресса. Поэтому, в первую очередь, в преподавании данной
дисциплины следует обратить внимание на привитие у студентов навыков нестандартного мышления
при решении задач, позволяющих достигать поставленных целей с наименьшими затратами всех
видов ресурсов.